Wzory na pole powierzchni bocznej walca i stożka klucz do zrozumienia brył obrotowych
- Pole powierzchni bocznej walca obliczysz ze wzoru: Pb = 2πrh, gdzie 'r' to promień podstawy, a 'h' to wysokość walca.
- Dla stożka stosuje się wzór: Pb = πrl, gdzie 'r' to promień podstawy, a 'l' to tworząca stożka.
- Tworząca 'l' w stożku często wymaga wcześniejszego obliczenia z twierdzenia Pitagorasa: l² = H² + r², gdy znasz wysokość (H) i promień (r).
- Kluczowe jest rozróżnienie między wysokością stożka (H) a jego tworzącą (l), która jest "skośną krawędzią".
- Wizualizacja siatek brył (walec: prostokąt, stożek: wycinek koła) pomaga zrozumieć, skąd biorą się wzory.
- Pamiętaj, aby zawsze podawać wyniki w jednostkach kwadratowych (np. cm², m²).
Zacznijmy od podstaw. Czym właściwie jest powierzchnia boczna walca czy stożka? Wyobraź sobie puszkę po napoju. Jej powierzchnia boczna to ta część, którą trzymasz w dłoni bez górnego i dolnego wieczka. Podobnie ze stożkiem, na przykład z imprezową czapeczką. Powierzchnia boczna to ta kolorowa część, która okrywa głowę, bez okrągłej podstawy.
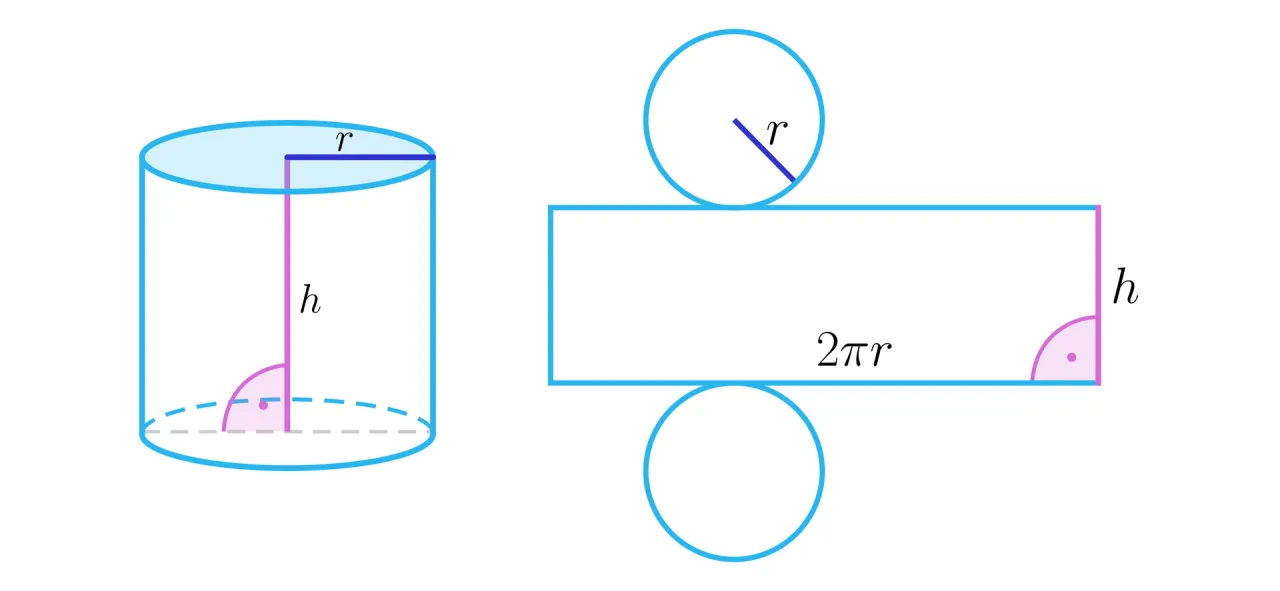
Aby lepiej zrozumieć te powierzchnie, warto spojrzeć na siatki brył. Siatka walca składa się z dwóch kół (podstawy) i prostokąta. Ten prostokąt to właśnie rozwinięta powierzchnia boczna walca. Jego jeden bok to wysokość walca (h), a drugi to obwód podstawy (2πr).
Siatka stożka jest nieco bardziej złożona. Składa się z koła (podstawy) i wycinka koła. Ten wycinek koła to nic innego jak rozwinięta powierzchnia boczna stożka. Jego promień to tworząca stożka (l), a długość łuku to obwód podstawy stożka (2πr).
Ważne jest, aby rozróżnić wysokość (oznaczaną jako 'h' dla walca i 'H' dla stożka) od tworzącej (oznaczanej jako 'l' dla stożka). W walcu wysokość 'h' jest prostopadła do podstaw, a w zasadzie jest "tworzącą" walca, bo każdy odcinek łączący odpowiadające sobie punkty na okręgach podstaw ma tę samą długość i jest prostopadły do podstaw. Natomiast w stożku wysokość 'H' to odcinek od wierzchołka do środka podstawy, prostopadły do niej. Tworząca 'l' to z kolei odcinek łączący wierzchołek stożka z dowolnym punktem na okręgu podstawy. Jest to ta "ukośna" krawędź stożka, która odgrywa kluczową rolę w obliczeniach.
Odkryj wzór na pole powierzchni bocznej walca
Obliczenie pola powierzchni bocznej walca jest stosunkowo proste, gdy tylko zrozumiesz jego siatkę. Jak już wspomniałem, powierzchnia boczna walca po rozwinięciu tworzy prostokąt. Jeden bok tego prostokąta to wysokość walca (h), a drugi bok to długość okręgu podstawy, czyli jego obwód (2πr). Zatem, aby obliczyć pole tego prostokąta, wystarczy pomnożyć długości jego boków. Stąd bierze się wzór na pole powierzchni bocznej walca:Pb = 2πrh
- r: To promień podstawy walca. Pamiętaj, że promień to połowa średnicy. Jeśli masz podaną średnicę, podziel ją przez dwa, aby uzyskać 'r'.
- h: To wysokość walca. Jest to odległość między dwiema podstawami walca.
- π (pi): To stała matematyczna, w przybliżeniu równa 3.14. W zadaniach często zostawia się ją we wzorze lub używa jej przybliżonej wartości.
Przyjrzyjmy się praktycznemu przykładowi. Załóżmy, że chcemy obliczyć, ile etykiety potrzeba na puszkę z napojem, która ma kształt walca.
- Dane: Promień podstawy puszki (r) wynosi 3 cm, a jej wysokość (h) to 12 cm.
- Wzór: Pb = 2πrh
- Podstawiamy wartości: Pb = 2 * π * 3 cm * 12 cm
- Obliczamy: Pb = 72π cm²
- Wynik: Jeśli chcemy podać wartość liczbową, używamy przybliżenia π ≈ 3.14. Wtedy Pb ≈ 72 * 3.14 cm² ≈ 226.08 cm².
Widzisz, to nic trudnego! Kluczem jest poprawne zidentyfikowanie promienia i wysokości.
Obliczanie pola powierzchni bocznej stożka bezbłędnie
Przejdźmy teraz do stożka. Pole powierzchni bocznej stożka, jak już wiesz, to wycinek koła. Wzór na jego pole jest nieco inny niż dla walca, ze względu na obecność tworzącej 'l'.
Pb = πrl
Najczęściej popełnianym błędem przy obliczaniu pola powierzchni bocznej stożka jest mylenie wysokości 'H' z tworzącą 'l'. Pamiętaj, że tworząca 'l' to odcinek łączący wierzchołek stożka z dowolnym punktem na okręgu podstawy. Jest to ta "ukośna" krawędź stożka. Co ważne, tworząca 'l', wysokość stożka 'H' i promień podstawy 'r' tworzą trójkąt prostokątny. W tym trójkącie wysokość 'H' i promień 'r' są przyprostokątnymi, a tworząca 'l' jest przeciwprostokątną. Oznacza to, że jeśli znasz wysokość i promień, możesz obliczyć tworzącą 'l' za pomocą twierdzenia Pitagorasa:
l² = H² + r²
Oto jak krok po kroku obliczyć tworzącą 'l':
- Zidentyfikuj dane: Masz podaną wysokość stożka (H) i promień podstawy (r).
- Zapisz twierdzenie Pitagorasa: l² = H² + r²
- Podstaw wartości: Wstaw znane wartości H i r do wzoru.
- Oblicz sumę kwadratów: H² + r²
- Wyciągnij pierwiastek kwadratowy: l = √(H² + r²)
Teraz, gdy rozumiemy tworzącą, przejdźmy do przykładu obliczenia pola powierzchni bocznej stożka. Wyobraź sobie imprezową czapeczkę w kształcie stożka.
- Dane: Wysokość czapeczki (H) wynosi 8 cm, a promień podstawy (r) to 6 cm.
-
Krok 1: Obliczamy tworzącą 'l' z twierdzenia Pitagorasa.
- l² = H² + r²
- l² = (8 cm)² + (6 cm)²
- l² = 64 cm² + 36 cm²
- l² = 100 cm²
- l = √100 cm²
- l = 10 cm
-
Krok 2: Obliczamy pole powierzchni bocznej stożka.
- Wzór: Pb = πrl
- Podstawiamy wartości: Pb = π * 6 cm * 10 cm
- Obliczamy: Pb = 60π cm²
- Wynik: Jeśli chcemy podać wartość liczbową, używamy przybliżenia π ≈ 3.14. Wtedy Pb ≈ 60 * 3.14 cm² ≈ 188.4 cm².
Jak widać, kluczowe jest to, aby najpierw upewnić się, że masz wszystkie potrzebne dane, a w przypadku stożka często oznacza to wcześniejsze obliczenie tworzącej 'l'.
Unikaj najczęstszych błędów przy obliczeniach
Podczas pracy z walcami i stożkami, łatwo wpaść w pewne pułapki. Jako osoba, która przez lata uczyła się i uczyła innych matematyki, mogę wskazać kilka najczęściej popełnianych błędów:
- Mylenie wysokości stożka (H) z tworzącą (l): To zdecydowanie numer jeden na liście. Zawsze pamiętaj, że 'H' to wysokość prostopadła, a 'l' to "ukośna" krawędź. Jeśli w zadaniu podano wysokość i promień, musisz obliczyć 'l' z Pitagorasa, zanim zastosujesz wzór na Pb stożka.
- Zapominanie o jednostkach kwadratowych: Pole powierzchni zawsze wyrażamy w jednostkach kwadratowych (np. cm², m², km²). Brak jednostek lub podanie ich w postaci liniowej (np. cm) to błąd.
- Błędne zaokrąglenia π: Jeśli w zadaniu nie jest podane konkretne zaokrąglenie dla π (np. 3.14 lub 22/7), najlepiej jest zostawić π we wzorze (np. 60π cm²). Jeśli musisz zaokrąglić, zawsze rób to na końcu obliczeń, aby uniknąć błędów kumulacyjnych.
- Błędne podstawienie wartości: Czasami w pośpiechu uczniowie podstawiają średnicę zamiast promienia 'r'. Zawsze upewnij się, że używasz promienia, który jest połową średnicy.
- Niezrozumienie siatki bryły: Brak wizualizacji siatki może prowadzić do niezrozumienia, skąd biorą się wzory. Jeśli masz problem, narysuj siatkę to naprawdę pomaga!
Walec i stożek: porównanie wzorów i kluczowe różnice
Podsumowując, zarówno walec, jak i stożek to fascynujące bryły, a ich pola powierzchni bocznych obliczamy, wykorzystując podobne, ale jednak różne zasady. Wzór na pole powierzchni bocznej walca to Pb = 2πrh, natomiast dla stożka to Pb = πrl. Wspólnym elementem obu wzorów jest promień podstawy 'r' oraz stała π. Kluczowa różnica polega na tym, że w walcu używamy wysokości 'h' (która jest odpowiednikiem tworzącej w tym kontekście), natomiast w stożku potrzebna jest tworząca 'l'. Pamiętaj, że tworząca 'l' w stożku często wymaga wcześniejszego obliczenia z twierdzenia Pitagorasa, co jest najważniejszym punktem, na który musisz zwrócić uwagę. Opanowanie tych wzorów i zrozumienie różnic między 'h' a 'l' to prosty sposób na sukces w geometrii!

