Obliczanie długości okręgu, czyli jego obwodu, to jedno z podstawowych zadań w geometrii, które ma szerokie zastosowanie w życiu codziennym i wielu dziedzinach nauki. W tym artykule pokażę Ci, jak krok po kroku, w prosty i zrozumiały sposób, wyznaczyć długość okręgu, mając dany promień. Skupimy się na kluczowym wzorze, zrozumieniu jego składników oraz przećwiczymy to na praktycznych przykładach, abyś poczuł się pewnie w tych obliczeniach.
Długość okręgu z promienia: kluczowe informacje o obliczeniach
- Podstawowy wzór na długość okręgu (L) to L = 2πr, gdzie r to promień, a π to stała matematyczna.
- Liczba Pi (π) to stała, najczęściej przybliżana jako 3,14, reprezentująca stosunek długości okręgu do jego średnicy.
- Promień (r) to odległość od środka okręgu do dowolnego punktu na jego brzegu.
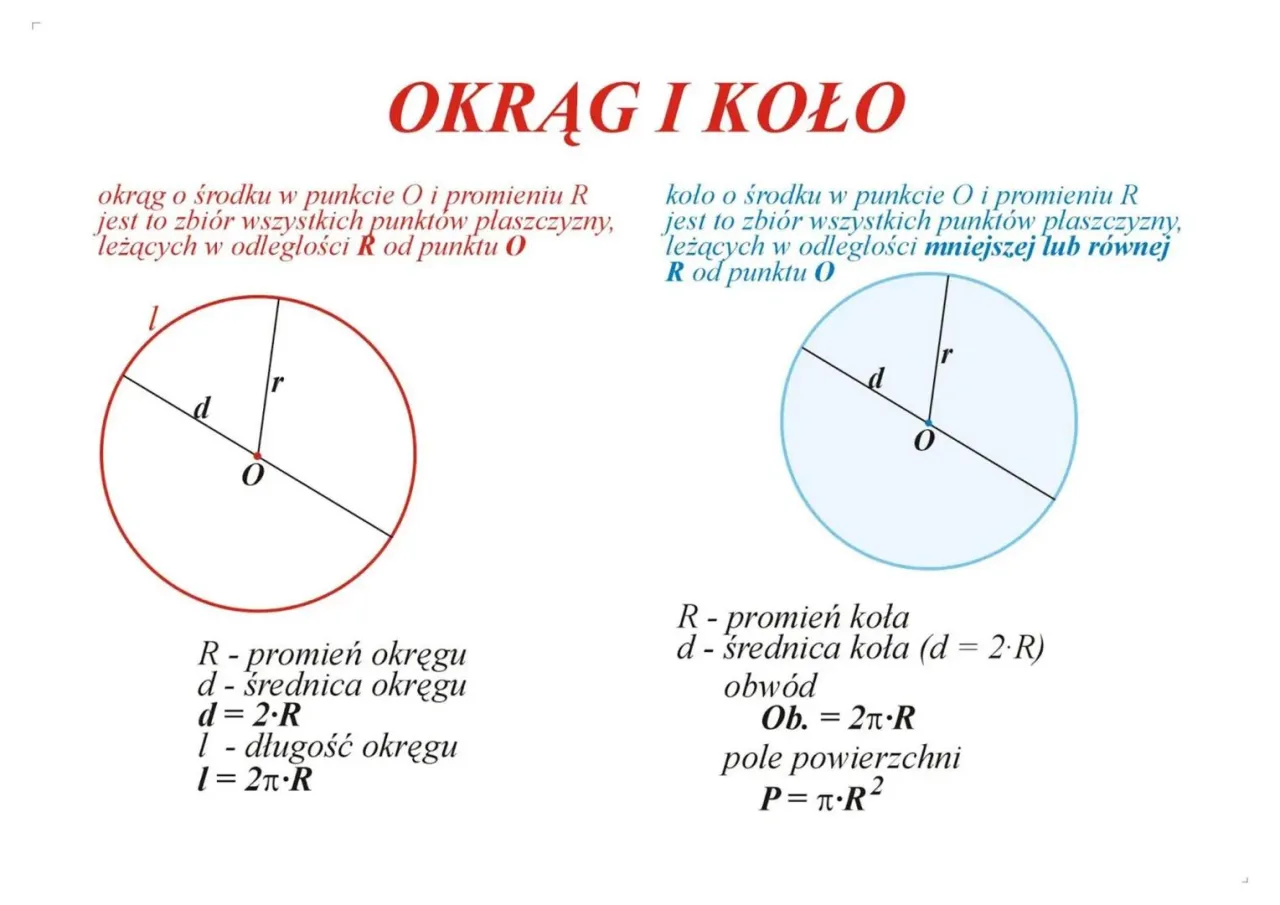
- Okrąg to linia (brzeg), a koło to okrąg wraz z jego wnętrzem; obliczamy długość okręgu.
- Najczęstsze błędy to mylenie promienia ze średnicą lub używanie wzoru na pole koła.
- Obliczanie długości okręgu ma praktyczne zastosowania, np. w projektowaniu czy inżynierii.
Zrozumieć długość okręgu i rolę promienia
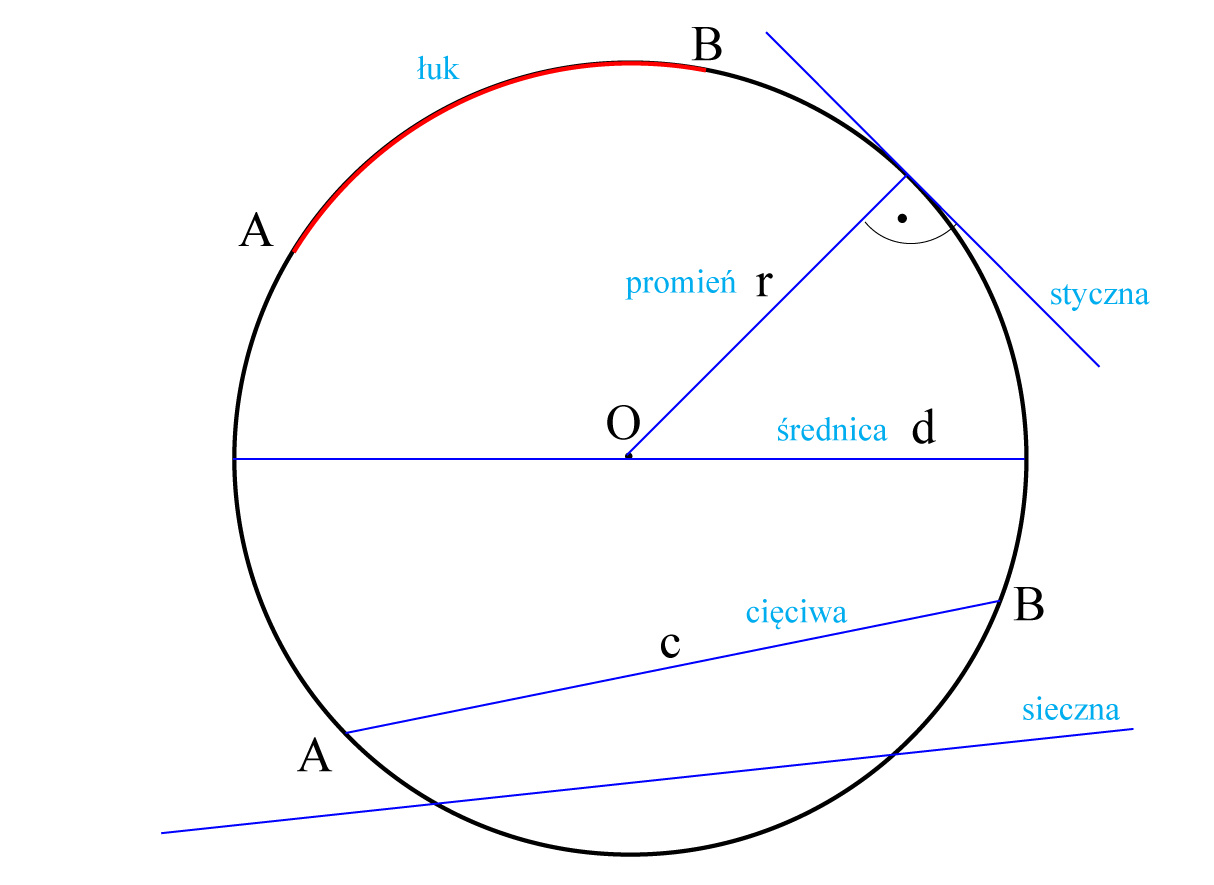
Długość okręgu to nic innego jak jego obwód miara "brzegu" tej figury geometrycznej. Wyobraź sobie, że rozcinasz okrąg i rozkładasz go na prostą linię. Długość tej linii to właśnie długość okręgu. Aby ją obliczyć, potrzebujemy kluczowej informacji: promienia. Promień jest fundamentem, na którym opierają się wszystkie obliczenia związane z okręgiem, ponieważ to on definiuje jego rozmiar.
Rozróżnienie, które ma znaczenie: okrąg kontra koło
W matematyce precyzja jest kluczowa, dlatego ważne jest, aby rozróżnić okrąg od koła. Okrąg to sama linia, czyli brzeg figury coś, co możesz narysować cyrklem. Natomiast koło to okrąg wraz z jego wnętrzem, czyli cała powierzchnia ograniczona tym okręgiem. Kiedy mówimy o "długości", zawsze mamy na myśli długość okręgu, a nie koła. Koło ma powierzchnię (pole), a okrąg ma długość (obwód). To rozróżnienie jest fundamentalne dla prawidłowego zrozumienia tematu.
Zrozumieć promień fundament Twoich obliczeń
Promień, oznaczany literą r (od angielskiego "radius"), to odległość od środka okręgu do dowolnego punktu leżącego na jego brzegu. Jest to podstawowy parametr, który określa rozmiar okręgu. Średnica, oznaczana literą d, to odcinek łączący dwa punkty na okręgu i przechodzący przez jego środek. Jest to najdłuższa cięciwa okręgu. Co ważne, średnica jest zawsze dwukrotnością promienia, czyli d = 2r. Zrozumienie tej zależności jest niezwykle ważne, ponieważ pozwala nam swobodnie przechodzić między tymi dwoma miarami w obliczeniach.Czym jest tajemnicza liczba Pi (π) i jaką rolę odgrywa?
Liczba Pi, oznaczana grecką literą π, to jedna z najbardziej fascynujących stałych matematycznych. Jest to stosunek długości dowolnego okręgu do jego średnicy. Niezależnie od tego, jak duży lub mały jest okrąg, ten stosunek zawsze będzie taki sam i wynosi właśnie Pi. Pi jest liczbą niewymierną, co oznacza, że ma nieskończone rozwinięcie dziesiętne, które nigdy się nie powtarza. W praktycznych obliczeniach i zadaniach szkolnych najczęściej stosujemy jej przybliżenie: π ≈ 3,14, choć czasem używa się dokładniejszego 3,1416. Symbol π został spopularyzowany w XVIII wieku i pochodzi od pierwszej litery greckiego słowa "perimetron", oznaczającego obwód. Bez liczby Pi nie bylibyśmy w stanie precyzyjnie obliczyć długości okręgu.
Poznaj niezawodny wzór na długość okręgu
Kiedy już rozumiemy wszystkie podstawowe pojęcia, możemy przejść do sedna, czyli do wzoru, który pozwoli nam obliczyć długość okręgu. To prosta, ale niezwykle potężna formuła, która jest fundamentem geometrii.
Główny wzór: L = 2πr jak go interpretować?
Podstawowy i najbardziej uniwersalny wzór na długość okręgu, mając dany promień, wygląda następująco:
L = 2πr
Rozłóżmy go na czynniki pierwsze, abyś dokładnie wiedział, co oznacza każdy symbol:
- L: To symbol oznaczający długość okręgu, czyli jego obwód. Jest to wynik, którego szukamy.
- 2: To po prostu stała liczba, która wynika z relacji między promieniem a średnicą (średnica to dwa promienie).
- π (Pi): To wspomniana wcześniej stała matematyczna, której wartość w przybliżeniu wynosi 3,14.
- r: To promień okręgu, czyli odległość od jego środka do dowolnego punktu na brzegu.
W praktyce oznacza to, że aby obliczyć długość okręgu, wystarczy pomnożyć dwukrotność promienia przez liczbę Pi. Proste, prawda?
Przeczytaj również: Logarytmy dla opornych: Zrozum potęgi na nowo!
Dlaczego czasem spotykasz wzór L = πd i co on ma wspólnego z promieniem?
Możliwe, że spotkałeś się również z innym wzorem na długość okręgu: L = πd, gdzie "d" oznacza średnicę okręgu. Nie martw się, to nie jest żaden nowy, skomplikowany wzór! W rzeczywistości oba wzory są ze sobą tożsame i prowadzą do tego samego wyniku. Pamiętasz, że średnica (d) jest zawsze dwukrotnością promienia (r), czyli d = 2r? Właśnie dlatego! Jeśli podstawimy "2r" za "d" do wzoru L = πd, otrzymamy L = π(2r), co po prostu przestawiamy na L = 2πr. Zatem, niezależnie od tego, czy masz podany promień, czy średnicę, możesz łatwo obliczyć długość okręgu. Jeśli masz średnicę, możesz użyć L = πd, albo najpierw podzielić średnicę przez 2, aby uzyskać promień, a następnie zastosować L = 2πr. Wybór należy do Ciebie!
Jak obliczyć długość okręgu krok po kroku
Teraz, gdy znamy już teorię i wzory, przejdźmy do praktyki. Przedstawię Ci prosty, czterostopniowy proces, który pozwoli Ci bezbłędnie obliczyć długość każdego okręgu, mając dany promień.
- Upewnij się, że znasz wartość promienia (r). To pierwszy i najważniejszy krok. Sprawdź dokładnie, czy podana wartość to promień (od środka do brzegu), a nie średnica (przez środek, od brzegu do brzegu). Jeśli masz podaną średnicę, po prostu podziel ją przez dwa, aby uzyskać promień (r = d/2).
- Przyjmij właściwe przybliżenie liczby Pi (najczęściej π ≈ 3,14). W większości zadań matematycznych i praktycznych obliczeń wystarczające jest użycie Pi z dokładnością do dwóch miejsc po przecinku, czyli 3,14. Jeśli zadanie wymaga większej precyzji, może być podane inne przybliżenie (np. 3,1416).
- Podstaw wartości do wzoru i wykonaj mnożenie. Użyj wzoru L = 2πr. W miejsce "r" wstaw znaną wartość promienia, a w miejsce "π" przyjęte przybliżenie. Następnie pomnóż te trzy liczby: 2 * π * r.
- Zapisz wynik z prawidłową jednostką. Długość okręgu powinna być wyrażona w tej samej jednostce, w której podany był promień. Jeśli promień był w centymetrach (cm), wynik będzie w centymetrach. Jeśli w metrach (m), wynik będzie w metrach. Nie zapomnij o jednostce, bo bez niej wynik jest niekompletny!
Przykłady obliczeń długości okręgu w praktyce
Teoria jest ważna, ale to praktyka utrwala wiedzę. Przyjrzyjmy się kilku przykładom, które pomogą Ci zrozumieć, jak zastosować wzór L = 2πr w różnych sytuacjach.
Przykład 1: Obliczanie obwodu tarczy do darta o promieniu 22,5 cm.
Dane: Promień (r) = 22,5 cm. Przyjmujemy π ≈ 3,14.
Wzór: L = 2πr
Rozwiązanie:
L = 2 * 3,14 * 22,5 cm
L = 6,28 * 22,5 cm
L = 141,3 cm
Odpowiedź: Długość okręgu tarczy do darta wynosi 141,3 cm.
Przykład 2: Ile metrów siatki potrzeba na ogrodzenie okrągłego klombu o promieniu 3 m?
Dane: Promień (r) = 3 m. Przyjmujemy π ≈ 3,14.
Wzór: L = 2πr
Rozwiązanie:
L = 2 * 3,14 * 3 m
L = 6,28 * 3 m
L = 18,84 m
Odpowiedź: Na ogrodzenie klombu potrzeba 18,84 metra siatki.
Przykład 3: Jaką drogę pokona koło rowerowe (promień 35 cm) podczas jednego obrotu?
Dane: Promień (r) = 35 cm. Przyjmujemy π ≈ 3,14.
Wzór: L = 2πr
Rozwiązanie:
L = 2 * 3,14 * 35 cm
L = 6,28 * 35 cm
L = 219,8 cm
Odpowiedź: Koło rowerowe podczas jednego obrotu pokona drogę 219,8 cm (czyli 2,198 metra).
Unikaj najczęstszych błędów przy obliczaniu długości okręgu
Nawet proste obliczenia mogą prowadzić do błędów, jeśli nie będziemy uważni. Oto najczęstsze pułapki, na które warto zwrócić uwagę, oraz wskazówki, jak ich unikać:
- Mylenie promienia ze średnicą: To absolutnie najczęstszy błąd. Jeśli masz podaną średnicę (d), a użyjesz jej jako promienia (r) we wzorze L = 2πr, Twój wynik będzie dwukrotnie za duży. Zawsze upewnij się, czy podana wartość to promień, czy średnica. Pamiętaj, że promień to połowa średnicy (r = d/2).
- Używanie wzoru na pole koła (P = πr²): Często widzę, jak ludzie mylą wzory na obwód (długość okręgu) i pole powierzchni koła. Wzór na pole to P = πr², a na długość okręgu to L = 2πr. Są to zupełnie różne formuły, służące do obliczania różnych właściwości. Zawsze sprawdzaj, czy używasz właściwego wzoru do właściwego celu.
- Błędne jednostki: Zapominanie o jednostkach lub używanie ich w sposób niekonsekwentny to kolejny częsty błąd. Jeśli promień jest w centymetrach, długość okręgu również będzie w centymetrach. Jeśli promień jest w metrach, wynik będzie w metrach. Zawsze podawaj wynik z prawidłową jednostką i upewnij się, że jest ona zgodna z jednostką promienia.
- Nieprawidłowe przybliżenie liczby Pi: Chociaż 3,14 jest najczęściej wystarczające, w niektórych zadaniach (zwłaszcza inżynierskich czy naukowych) może być wymagane dokładniejsze przybliżenie Pi. Zawsze sprawdzaj, czy w treści zadania nie ma wskazówek dotyczących precyzji Pi. Jeśli nie ma, 3,14 jest bezpiecznym wyborem.
Praktyczne zastosowania obliczania długości okręgu
Może się wydawać, że obliczanie długości okręgu to tylko szkolne zadanie, ale w rzeczywistości ma ono mnóstwo praktycznych zastosowań w naszym codziennym życiu i w różnych branżach. Jako Igor Lis, mogę potwierdzić, że te podstawowe umiejętności są wykorzystywane znacznie częściej, niż myślimy:
- Budownictwo i inżynieria: Architekci i inżynierowie muszą obliczać długość okręgów przy projektowaniu okrągłych fundamentów, rur, tuneli, mostów czy kopuł. Wiedza ta jest kluczowa do określenia ilości potrzebnego materiału (np. betonu, stali) lub długości obwodów.
- Projektowanie i produkcja: W produkcji przedmiotów codziennego użytku, takich jak koła zębate, obręcze, biżuteria, naczynia czy elementy maszyn, precyzyjne obliczanie długości okręgu jest niezbędne do zapewnienia odpowiedniego dopasowania i funkcjonalności.
- Rolnictwo i ogrodnictwo: Rolnicy i ogrodnicy mogą używać tych obliczeń do określania długości ogrodzenia potrzebnego do okrągłego klombu, pastwiska czy wyznaczania obszaru nawadniania przez obrotowe zraszacze.
- Sport: Długość okręgu jest kluczowa przy projektowaniu bieżni na stadionach, torów kolarskich czy basenów o okrągłym kształcie, aby zapewnić standardowe odległości dla sportowców.
- Krawiectwo i rzemiosło: Krawcowe i rzemieślnicy obliczają długość okręgu, aby określić, ile materiału (np. koronki, taśmy) potrzeba do obszycia okrągłego obrusu, serwetki czy kapelusza.
- Transport: Obliczanie drogi pokonywanej przez koło pojazdu podczas jednego obrotu (co jest właśnie długością okręgu koła) jest fundamentalne w mechanice i projektowaniu pojazdów.

