Jak obliczyć wysokość w trójkącie równobocznym? Wzór i Pitagoras

Ten artykuł szczegółowo wyjaśni, czym jest wysokość w trójkącie równobocznym, przedstawiając gotowy wzór, krok po kroku tłumacząc jego wyprowadzenie oraz pokazując praktyczne zastosowania w zadaniach matematycznych. Poznaj klucz do zrozumienia geometrii trójkątów równobocznych.

Wprowadzenie do wysokości w trójkącie równobocznym

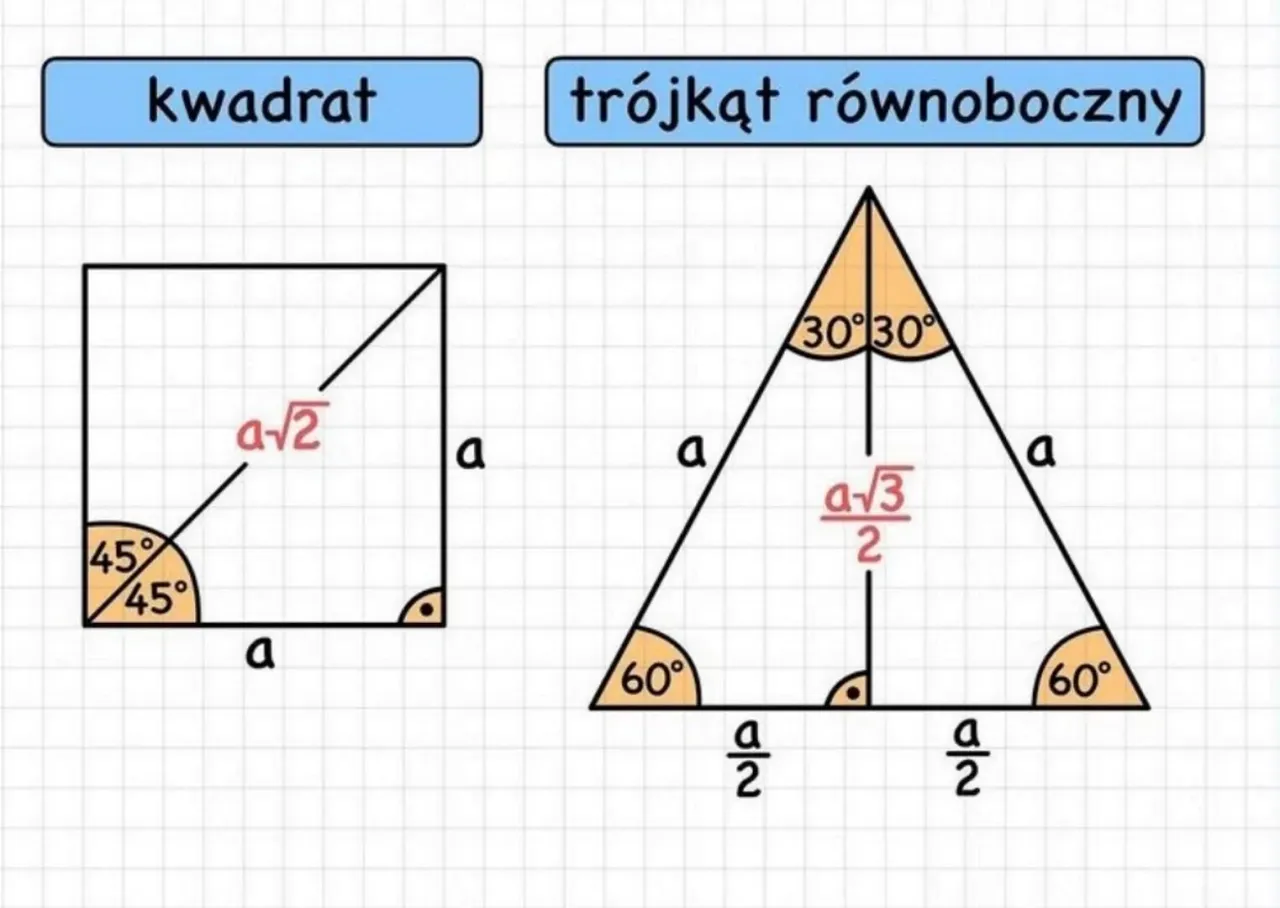
Trójkąt równoboczny to jedna z najbardziej symetrycznych i fundamentalnych figur w geometrii. Charakteryzuje się tym, że wszystkie jego boki mają jednakową długość, a wszystkie kąty wewnętrzne są równe i wynoszą po 60 stopni. Ta szczególna symetria sprawia, że wiele jego właściwości jest łatwych do wyprowadzenia i zrozumienia, a wysokość jest jednym z kluczowych elementów, które pozwalają nam zgłębić jego naturę.

Wysokość w trójkącie równobocznym to odcinek poprowadzony z wierzchołka prostopadle do przeciwległego boku. Co istotne, w trójkącie równobocznym każda wysokość jest jednocześnie środkową (dzieli przeciwległy bok na dwie równe części) i dwusieczną kąta, z którego wychodzi. Długość wysokości (oznaczanej jako 'h') w trójkącie równobocznym o boku długości 'a' można obliczyć za pomocą następującego wzoru: `h = (a√3) / 2`. Symbol 'a' oznacza tutaj długość dowolnego boku trójkąta, a 'h' to jego wysokość.

Wyprowadzenie wzoru na wysokość z twierdzenia Pitagorasa

Zrozumienie, skąd bierze się dany wzór, jest często ważniejsze niż samo jego zapamiętanie. Wzór na wysokość w trójkącie równobocznym jest doskonałym przykładem zastosowania twierdzenia Pitagorasa. Przyjrzyjmy się temu krok po kroku:

1. Wyobraźmy sobie trójkąt równoboczny o boku długości 'a'. Kiedy narysujemy jedną z wysokości 'h' z dowolnego wierzchołka do przeciwległego boku, podzielimy ten trójkąt na dwa identyczne trójkąty prostokątne. To kluczowy krok, ponieważ twierdzenie Pitagorasa stosuje się właśnie do trójkątów prostokątnych.

2. Spójrzmy na jeden z tych trójkątów prostokątnych. Jego przeciwprostokątną jest bok trójkąta równobocznego, czyli 'a'. Jedna z przyprostokątnych to nasza wysokość 'h'. Druga przyprostokątna to połowa boku trójkąta równobocznego, ponieważ wysokość w trójkącie równobocznym dzieli podstawę na dwie równe części. Zatem jej długość wynosi `a/2`.

3. Teraz możemy zastosować twierdzenie Pitagorasa, które mówi, że w trójkącie prostokątnym suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej. W naszym przypadku wygląda to tak:

   (a/2)² + h² = a²

4. Pozostaje nam przekształcić to równanie, aby wyznaczyć 'h'.

   • Najpierw podnosimy `a/2` do kwadratu: `a²/4 + h² = a²`
   • Następnie odejmujemy `a²/4` od obu stron równania: `h² = a² - a²/4`
   • Upraszczamy prawą stronę: `h² = 4a²/4 - a²/4`
   • `h² = 3a²/4`
   • Na koniec pierwiastkujemy obie strony, aby pozbyć się kwadratu przy 'h': `h = √(3a²/4)`
   • Wyciągamy pierwiastek z licznika i mianownika: `h = (√3 * √a²) / √4`
   • Ostatecznie otrzymujemy wzór: `h = (a√3) / 2`.

   Jak widać, wyprowadzenie jest logiczne i opiera się na podstawowych zasadach geometrii i algebry.

Praktyczne zastosowanie wzoru na wysokość

Wzór na wysokość jest niezwykle przydatny w wielu zadaniach matematycznych. Pokażę Ci teraz, jak go używać w praktyce, zarówno do obliczania wysokości, jak i innych elementów trójkąta równobocznego.

1. Zadanie: Oblicz wysokość (h), mając dany bok (a) trójkąta równobocznego.
Załóżmy, że mamy trójkąt równoboczny o boku `a = 6 cm`. Chcemy obliczyć jego wysokość.
Korzystamy ze wzoru: `h = (a√3) / 2`
Podstawiamy wartość 'a': `h = (6√3) / 2`
Upraszczamy: `h = 3√3 cm`
Wynik: Wysokość trójkąta wynosi 3√3 cm.

2. Zadanie: Oblicz długość boku (a), mając daną wysokość (h) trójkąta równobocznego.
Przypuśćmy, że wysokość trójkąta równobocznego wynosi `h = 4√3 cm`. Jakiej długości jest jego bok?
Zaczynamy od wzoru na wysokość: `h = (a√3) / 2`
Teraz musimy przekształcić wzór, aby wyznaczyć 'a'.
Mnożymy obie strony przez 2: `2h = a√3`
Dzielimy obie strony przez √3: `a = (2h) / √3`
Podstawiamy wartość 'h': `a = (2 * 4√3) / √3`
Upraszczamy (√3 w liczniku i mianowniku się skraca): `a = 2 * 4`
`a = 8 cm`
Wynik: Długość boku trójkąta wynosi 8 cm.

3. Zadanie: Oblicz pole trójkąta równobocznego, wykorzystując wysokość (h).
Wykorzystajmy wysokość z Zadania 1, czyli `h = 3√3 cm`, oraz bok `a = 6 cm`. Wzór na pole trójkąta to `P = (podstawa * wysokość) / 2`.
W naszym przypadku podstawa to 'a', a wysokość to 'h'.
`P = (a * h) / 2`
Podstawiamy wartości: `P = (6 * 3√3) / 2`
`P = (18√3) / 2`
`P = 9√3 cm²`
Wynik: Pole trójkąta wynosi 9√3 cm².

Najczęstsze błędy i jak ich unikać

Podczas pracy z wysokością w trójkącie równobocznym, łatwo jest popełnić kilka typowych błędów. Jako Igor Lis, często widzę te same pomyłki u moich uczniów. Oto one, wraz z poradami, jak ich unikać:

• Pomyłki w kolejności działań przy kwadratowaniu `a/2`: Często zdarza się, że zamiast `(a/2)² = a²/4`, uczniowie zapisują `a²/2`. Pamiętaj, że kwadrat dotyczy zarówno licznika, jak i mianownika ułamka. Zawsze kwadratuj całe wyrażenie w nawiasie.

• Zapominanie o pierwiastku z 3 lub błędne jego traktowanie: Pierwiastek z 3 (`√3`) jest integralną częścią wzoru. Nie można go po prostu pominąć. Jeśli wynik ma być w postaci dziesiętnej, dopiero na samym końcu podstawiamy jego przybliżoną wartość (ok. 1.732). W przeciwnym razie zostawiamy go w postaci pierwiastka.

• Błędy przy przekształcaniu wzoru w celu obliczenia boku 'a': Odwracanie wzoru `h = (a√3) / 2` na `a = (2h) / √3` wymaga ostrożności. Częstym błędem jest zapominanie o pomnożeniu 'h' przez 2 lub błędne dzielenie. Zawsze wykonuj przekształcenia krok po kroku, mnożąc lub dzieląc obie strony równania.

• Błędy w obliczeniach z pierwiastkami: Pamiętaj, że `√3 * √3 = 3`. Jeśli w mianowniku pojawi się `√3`, warto usunąć niewymierność, mnożąc licznik i mianownik przez `√3`. Na przykład: `(2h) / √3 = (2h√3) / 3`.

Wysokość a inne elementy trójkąta równobocznego

Wysokość w trójkącie równobocznym to nie tylko odcinek, ale także klucz do zrozumienia wielu innych właściwości tej figury. Jej związki z innymi elementami są fascynujące i bardzo przydatne w rozwiązywaniu złożonych zadań:

• Związek wysokości z polem trójkąta: Wysokość jest niezbędna do obliczenia pola trójkąta. Standardowy wzór na pole to `P = (a * h) / 2`. Jeśli podstawimy do niego wzór na 'h', otrzymamy popularny wzór na pole trójkąta równobocznego wyrażony tylko przez długość boku: `P = (a * (a√3)/2) / 2 = (a²√3) / 4`. To pokazuje, jak wzory są ze sobą powiązane.

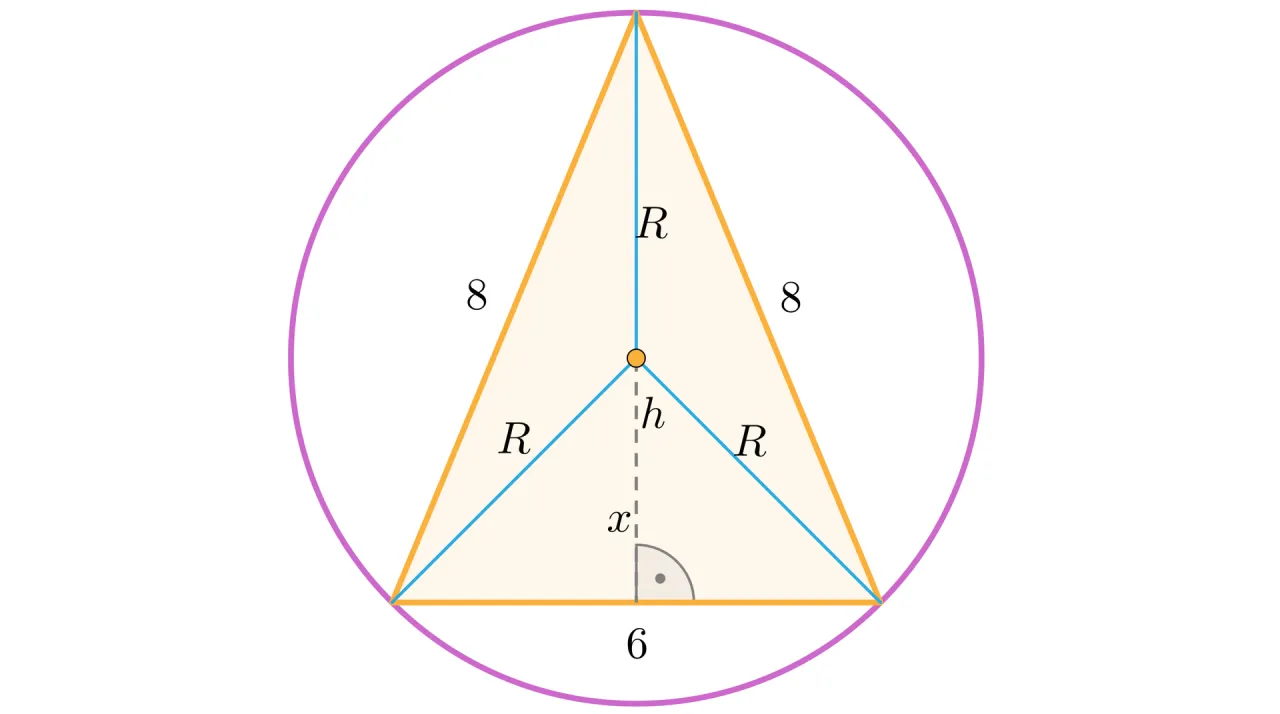
• Relacje wysokości z promieniami okręgu wpisanego i opisanego: W trójkącie równobocznym punkt przecięcia wysokości jest jednocześnie środkiem okręgu wpisanego i opisanego. Istnieją proste zależności między wysokością a promieniami tych okręgów:
  • Promień okręgu wpisanego (r) wynosi `r = (1/3)h`.
  • Promień okręgu opisanego (R) wynosi `R = (2/3)h`.

  Zauważ, że `R = 2r`, co jest unikalną cechą trójkąta równobocznego.

• Znaczenie punktu przecięcia wysokości: Wszystkie trzy wysokości w trójkącie równobocznym są równej długości i przecinają się w jednym punkcie. Ten punkt jest niezwykle ważny, ponieważ jest jednocześnie:

  • Ortocentrum (punkt przecięcia wysokości).
  • Środkiem ciężkości (punkt przecięcia środkowych).
  • Środkiem okręgu wpisanego (punkt równo odległy od boków).
  • Środkiem okręgu opisanego (punkt równo odległy od wierzchołków).
  Co więcej, ten punkt dzieli każdą z wysokości w stosunku 2:1, licząc od wierzchołka. Dłuższy odcinek (2/3h) to promień okręgu opisanego (R), a krótszy (1/3h) to promień okręgu wpisanego (r).