W tym artykule dowiesz się, jak krok po kroku rysować siatki graniastosłupów i ostrosłupów, co pozwoli Ci lepiej zrozumieć geometrię przestrzenną i uniknąć typowych błędów. To praktyczny przewodnik, który pomoże Ci opanować tę umiejętność, niezbędną zarówno w szkole, jak i w codziennym życiu.
Rysowanie siatek graniastosłupów i ostrosłupów klucz do zrozumienia geometrii przestrzennej krok po kroku
- Siatka to rozłożona bryła na płaszczyźnie, kluczowa do wizualizacji i budowy modeli 3D.
- Do rysowania potrzebujesz ołówka, linijki, ekierki i cyrkla; papier w kratkę znacząco ułatwia pracę.
- Graniastosłupy charakteryzują się dwiema podstawami i prostokątnymi ścianami bocznymi, natomiast ostrosłupy mają jedną podstawę i trójkątne ściany zbiegające się w wierzchołku.
- Pamiętaj o precyzji w mierzeniu i sprawdzeniu, czy wszystkie krawędzie siatki stykają się prawidłowo jedna bryła może mieć wiele poprawnych siatek.
- Artykuł szczegółowo pokaże rysowanie siatek dla najpopularniejszych brył: sześcianów, prostopadłościanów, graniastosłupów i ostrosłupów o podstawach trójkątnych, kwadratowych i sześciokątnych.
Czym właściwie jest siatka i po co ją rysujemy?
Siatka bryły geometrycznej to nic innego jak jej rozłożona powierzchnia na płaszczyźnie. Wyobraź sobie kartonowe pudełko, które rozcinasz wzdłuż krawędzi i rozkładasz na płasko to właśnie jest jego siatka. Dla mnie, jako osoby zajmującej się geometrią, siatka jest absolutnie kluczowa do wizualizacji brył 3D w dwóch wymiarach. Pomaga zrozumieć, z jakich elementów składa się dana bryła i jak te elementy do siebie pasują.
Po co ją rysujemy? Przede wszystkim, jest to podstawa programowa w szkołach, ale jej znaczenie wykracza daleko poza salę lekcyjną. Umiejętność rysowania siatek jest niezbędna przy tworzeniu modeli kartonowych, projektowaniu opakowań, a także w bardziej zaawansowanych dziedzinach, takich jak grafika 3D czy architektura. Dzięki siatkom możemy precyzyjnie obliczyć pole powierzchni bryły, co jest niezwykle przydatne w praktyce.Graniastosłup a ostrosłup: fundamentalne różnice, które musisz znać przed rysowaniem
Zanim zabierzemy się za rysowanie, musimy jasno rozróżnić graniastosłupy od ostrosłupów. To fundamentalna wiedza, która wpływa na całą konstrukcję siatki. Ja zawsze tłumaczę moim uczniom, że te dwie bryły to jak dwie różne rodziny, choć mają pewne wspólne cechy.
Główna różnica leży w ich budowie:
| Cecha | Graniastosłup | Ostrosłup |
|---|---|---|
| Liczba podstaw | Dwie, identyczne i równoległe | Jedna |
| Kształt ścian bocznych | Zawsze prostokątne (lub równoległoboki w graniastosłupach pochyłych), łączące podstawy | Zawsze trójkątne, zbiegające się w jednym punkcie (wierzchołku) |
| Wierzchołek | Brak wspólnego wierzchołka dla ścian bocznych | Jeden wspólny wierzchołek, w którym spotykają się wszystkie ściany boczne |
Jak widzisz, te różnice mają bezpośrednie przełożenie na wygląd siatki. Siatka graniastosłupa będzie miała dwie podstawy i pas prostokątnych ścian bocznych pomiędzy nimi, natomiast siatka ostrosłupa jedną podstawę i trójkątne ściany boczne "rozchodzące się" od niej i łączące się w jednym punkcie.
Jakie przybory przygotować, by rysowanie stało się prostsze?
Precyzja to podstawa w rysowaniu siatek. Bez odpowiednich narzędzi trudno będzie Ci osiągnąć zadowalający efekt. Z mojego doświadczenia wiem, że warto zainwestować w kilka podstawowych przyborów, które znacząco ułatwią pracę:
- Ołówek: Wybierz ołówek o średniej twardości (np. HB lub B), który pozwoli na rysowanie wyraźnych, ale łatwych do wymazania linii.
- Linijka: Długa, prosta linijka (np. 30 cm) to absolutny must-have do rysowania prostych krawędzi i mierzenia odległości.
- Ekierka: Niezbędna do rysowania kątów prostych, co jest kluczowe przy ścianach prostokątnych graniastosłupów i przy prostopadłych krawędziach podstaw.
- Cyrkiel: Będzie Ci potrzebny do rysowania okręgów i wyznaczania wierzchołków wielokątów foremnych (np. trójkątów równobocznych, sześciokątów). To narzędzie gwarantuje precyzję, której nie da się osiągnąć "na oko".
Dodatkowo, gorąco polecam papier w kratkę. To naprawdę duże ułatwienie! Kratki pomagają w zachowaniu precyzji, proporcji i prostych kątów, dzięki czemu łatwiej jest liczyć jednostki i utrzymywać równoległość linii. Spróbuj, a zobaczysz różnicę!
Graniastosłupy: rysowanie siatek krok po kroku
Zaczynamy od podstawy: jak poprawnie narysować fundament Twojej bryły?
Rysowanie siatki zawsze zaczynamy od podstawy. To fundament całej bryły, więc jej precyzyjne wykonanie jest absolutnie kluczowe. Niezależnie od tego, czy rysujesz kwadrat, trójkąt równoboczny czy sześciokąt, musisz zadbać o dokładne wymiary i kąty. Ja zawsze radzę, aby najpierw narysować jedną podstawę, a dopiero potem resztę siatki.
Na przykład, jeśli rysujesz podstawę kwadratową, użyj linijki i ekierki, aby upewnić się, że wszystkie boki są równe, a wszystkie kąty mają dokładnie 90 stopni. Przy trójkącie równobocznym, cyrkiel będzie Twoim najlepszym przyjacielem do wyznaczenia wierzchołków i zapewnienia równych boków.Graniastosłup prawidłowy czworokątny (sześcian i prostopadłościan): najprostszy przykład na start
Sześcian i prostopadłościan to idealne bryły do rozpoczęcia przygody z rysowaniem siatek graniastosłupów. Są proste, intuicyjne i pozwalają zrozumieć podstawowe zasady. Pamiętaj, że sześcian to w gruncie rzeczy szczególny przypadek prostopadłościanu, w którym wszystkie krawędzie mają tę samą długość. Jeśli opanujesz te, reszta będzie już tylko kwestią adaptacji.
Rysujemy siatkę sześcianu: więcej niż jeden poprawny sposób
Sześcian to bryła, która ma 6 identycznych ścian w kształcie kwadratów. Co ciekawe, istnieje wiele poprawnych sposobów na jej rozłożenie. Pokażę Ci kilka najpopularniejszych wariantów:
-
Wariant "krzyżowy":
- Narysuj jeden kwadrat (to będzie jedna ze ścian bocznych).
- Do każdego z czterech boków tego kwadratu dorysuj po jednym identycznym kwadracie. Powstanie kształt krzyża.
- Do jednego z zewnętrznych kwadratów (np. tego na górze lub na dole) dorysuj ostatni, szósty kwadrat. To będzie druga podstawa.
-
Wariant "liniowy":
- Narysuj cztery kwadraty obok siebie w jednej linii. To będą cztery ściany boczne.
- Do drugiego kwadratu od lewej (lub od prawej) dorysuj jeden kwadrat do góry i jeden kwadrat do dołu. Będą to podstawy.
-
Wariant "schody":
- Narysuj trzy kwadraty obok siebie.
- Do środkowego kwadratu dorysuj jeden kwadrat do góry i jeden do dołu.
- Do jednego z zewnętrznych kwadratów (np. tego po prawej) dorysuj jeden kwadrat do góry lub do dołu, tworząc "schodki".
Ważne jest, aby wszystkie kwadraty były identyczne i aby po złożeniu tworzyły zamkniętą bryłę. Wybierz ten wariant, który jest dla Ciebie najbardziej intuicyjny.
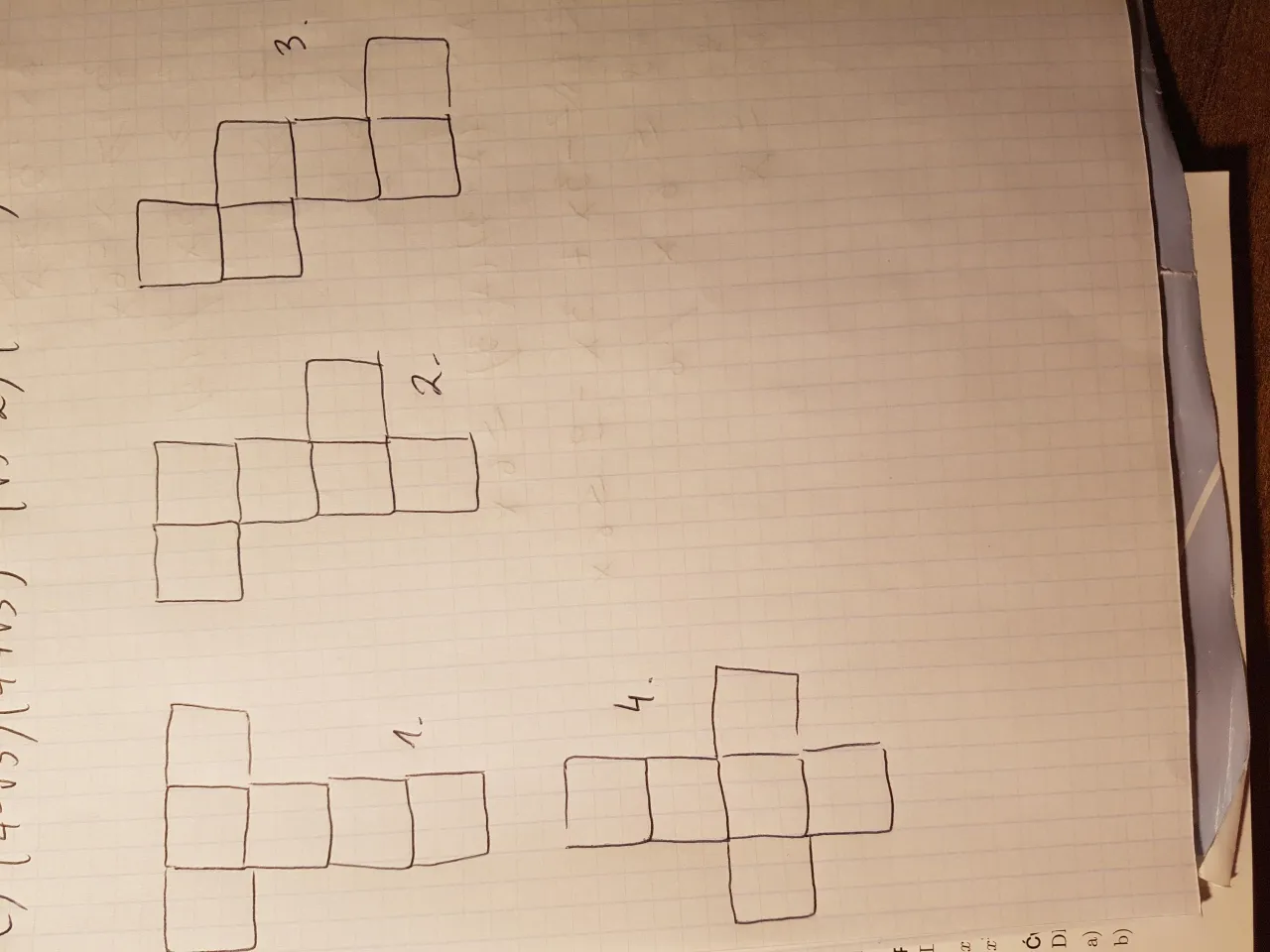
Siatka prostopadłościanu: na co zwrócić uwagę przy różnych długościach krawędzi?
Rysowanie siatki prostopadłościanu jest bardzo podobne do rysowania siatki sześcianu, ale wymaga jeszcze większej precyzji w mierzeniu. Tutaj krawędzie mają różne długości, co oznacza, że ściany boczne nie będą kwadratami, lecz prostokątami o różnych wymiarach. Zawsze zaczynam od narysowania jednej z podstaw. Załóżmy, że podstawa ma boki o długości 'a' i 'b', a wysokość prostopadłościanu to 'h'.
Narysuj prostokątną podstawę (a x b). Następnie, do każdego boku tej podstawy dorysuj prostokątne ściany boczne. Dwie ściany będą miały wymiary a x h, a dwie pozostałe b x h. Kluczowe jest, aby dokładnie odmierzyć te wysokości i szerokości. Na koniec, dorysuj drugą, identyczną podstawę (a x b) do jednej ze ścian bocznych, tak aby po złożeniu idealnie pasowała. Pamiętaj, że przeciwległe ściany boczne muszą być identyczne. Precyzja w mierzeniu jest tutaj absolutnie kluczowa nawet minimalny błąd sprawi, że siatka nie złoży się poprawnie.
Graniastosłup o podstawie trójkąta: instrukcja dla figury trójkątnej
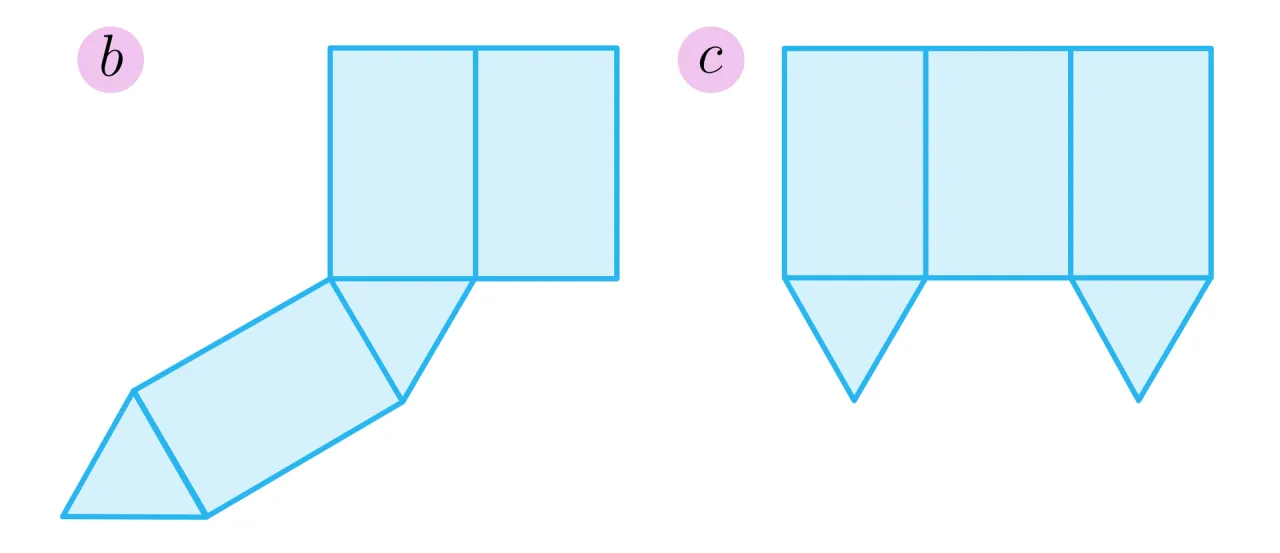
Graniastosłupy trójkątne są bardzo popularne w zadaniach szkolnych i stanowią kolejny ważny krok w nauce rysowania siatek. Ich siatki składają się z dwóch trójkątnych podstaw i trzech prostokątnych ścian bocznych. Skupimy się na graniastosłupie prawidłowym trójkątnym, czyli takim, którego podstawy są trójkątami równobocznymi.
Krok po kroku: siatka graniastosłupa prawidłowego trójkątnego
Oto jak narysować siatkę graniastosłupa prawidłowego trójkątnego:
- Narysuj jedną podstawę: Używając cyrkla i linijki, narysuj trójkąt równoboczny o zadanej długości boku (np. 'a'). To będzie pierwsza podstawa.
- Wyznacz ściany boczne: Do każdego z trzech boków trójkąta dorysuj prostokąt. Każdy z tych prostokątów będzie miał jeden bok o długości 'a' (czyli długości boku podstawy) i drugi bok o długości 'h' (wysokość graniastosłupa). Użyj ekierki, aby kąty były proste.
- Dorysuj drugą podstawę: Do jednego z prostokątów (ściany bocznej) dorysuj drugą, identyczną podstawę trójkątną. Upewnij się, że jest ona równoległa do pierwszej i że jej boki idealnie pasują do krawędzi prostokąta.
- Sprawdź połączenia: Wizualnie sprawdź, czy wszystkie krawędzie będą do siebie pasować po złożeniu. Trzy prostokątne ściany boczne powinny tworzyć "pas", a dwie trójkątne podstawy powinny być do niego dołączone.
Idziemy o krok dalej: siatka graniastosłupa o podstawie sześciokąta foremnego
Graniastosłupy sześciokątne to już nieco bardziej zaawansowane przykłady, ale ich rysowanie opiera się na tych samych zasadach. Kluczem jest tutaj precyzyjne narysowanie podstawy sześciokątnej foremnej, a następnie dopasowanie do niej sześciu prostokątnych ścian bocznych.
Jak użyć cyrkla do narysowania idealnej podstawy?
Narysowanie idealnego sześciokąta foremnego za pomocą cyrkla jest prostsze, niż myślisz:
- Narysuj okrąg: Otwórz cyrkiel na żądaną długość boku sześciokąta (np. 'a'). Narysuj okrąg.
- Wyznacz pierwszy punkt: Na okręgu zaznacz dowolny punkt. To będzie pierwszy wierzchołek sześciokąta.
- Odłóż długość boku: Nie zmieniając rozstawu cyrkla, wbij jego ostrze w zaznaczony punkt i odłóż tę samą długość na okręgu. Zaznacz nowy punkt.
- Powtórz czynność: Powtarzaj krok 3, wbijając ostrze cyrkla w nowo zaznaczony punkt, aż wyznaczysz wszystkie sześć wierzchołków. Ostatni punkt powinien idealnie zbiec się z pierwszym.
- Połącz wierzchołki: Za pomocą linijki połącz wszystkie sześć wierzchołków. Otrzymasz idealny sześciokąt foremny.
Prawidłowe rozmieszczenie sześciu ścian bocznych: uniknij typowych błędów
Po narysowaniu sześciokątnej podstawy, musisz do niej dołączyć sześć prostokątnych ścian bocznych i drugą podstawę. To tutaj często pojawiają się błędy, dlatego bądź szczególnie uważny:
- Pas ścian bocznych: Narysuj sześć identycznych prostokątów obok siebie, tworząc długi pas. Każdy prostokąt będzie miał szerokość równą długości boku sześciokąta ('a') i wysokość równą wysokości graniastosłupa ('h').
- Połączenie z podstawami: Do jednego z prostokątów w tym pasie dołącz jedną sześciokątną podstawę, a do innego (najczęściej przeciwległego lub sąsiedniego, ale tak, by siatka się nie "rozpadła") drugą podstawę. Upewnij się, że podstawy są umieszczone tak, aby po złożeniu znalazły się na przeciwległych końcach bryły.
- Precyzja kątów: Wszystkie kąty w prostokątnych ścianach bocznych muszą być proste. Używaj ekierki.
Moja rada: zawsze wyobraź sobie, jak ta siatka będzie się składać. Czy wszystkie krawędzie znajdą swoje "pary"? Czy podstawy będą równoległe?
Ostrosłupy: jak bezbłędnie narysować ich siatki?
Kluczowa różnica: jedna podstawa i zbiegające się ściany boczne
Przechodząc do ostrosłupów, musimy pamiętać o fundamentalnej różnicy w porównaniu do graniastosłupów: ostrosłup ma tylko jedną podstawę. Wszystkie jego ściany boczne są trójkątami i zbiegają się w jednym wspólnym punkcie, który nazywamy wierzchołkiem ostrosłupa. To właśnie ta cecha sprawia, że siatki ostrosłupów wyglądają zupełnie inaczej niż siatki graniastosłupów.
W siatce ostrosłupa zobaczymy jedną podstawę, a do jej krawędzi będą dołączone trójkątne ściany boczne, które po złożeniu spotkają się w jednym punkcie. Wymaga to dokładnego wyznaczenia długości krawędzi bocznych, co często jest wyzwaniem.
Ostrosłup prawidłowy czworokątny: siatka klasycznej piramidy
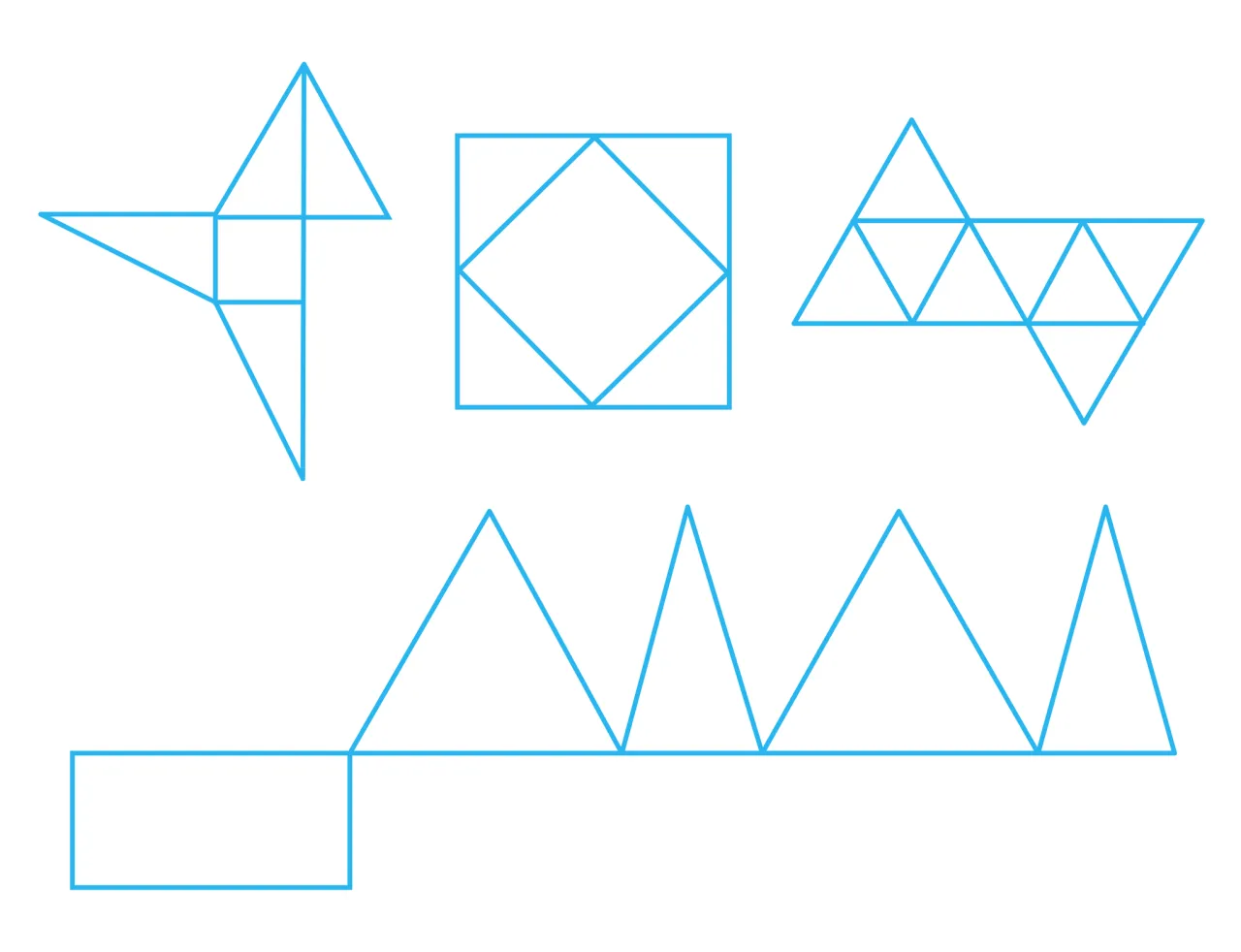
Ostrosłup prawidłowy czworokątny to nic innego jak klasyczna piramida, którą znamy z Egiptu. Jego podstawa jest kwadratem, a ściany boczne to cztery identyczne trójkąty równoramienne. To świetny przykład do nauki rysowania siatek ostrosłupów.
Rysujemy podstawę kwadratową i cztery identyczne trójkąty
Oto instrukcja rysowania siatki ostrosłupa prawidłowego czworokątnego:
- Narysuj podstawę: Narysuj kwadrat o zadanej długości boku (np. 'a'). To będzie podstawa ostrosłupa.
- Wyznacz punkty centralne boków: Zaznacz środki każdego z czterech boków kwadratu.
- Narysuj ściany boczne: Do każdego z boków kwadratu dorysuj trójkąt równoramienny. Podstawą każdego trójkąta będzie bok kwadratu ('a'). Ramiona tych trójkątów to krawędzie boczne ostrosłupa. Wszystkie cztery trójkąty muszą być identyczne.
- Upewnij się, że trójkąty się spotkają: Ważne jest, aby ramiona tych trójkątów miały taką samą długość, aby po złożeniu spotkały się w jednym punkcie wierzchołku ostrosłupa. Jak to zrobić precyzyjnie, wyjaśniam poniżej.
Jak poprawnie odmierzyć wysokość ścian bocznych?
To jest często problematyczny moment. Długość krawędzi bocznych ostrosłupa nie jest zazwyczaj podana bezpośrednio, ale wynika z wysokości ostrosłupa i długości krawędzi podstawy. Najprościej jest użyć cyrkla:
Po narysowaniu kwadratowej podstawy, musisz znać długość krawędzi bocznej ostrosłupa (oznaczmy ją jako 'k'). Jeśli nie jest podana, często można ją wyliczyć z twierdzenia Pitagorasa, znając wysokość ostrosłupa i połowę przekątnej podstawy. Gdy już masz tę długość, otwórz cyrkiel na długość 'k'. Wbij ostrze cyrkla w jeden z wierzchołków kwadratu i narysuj łuk. Następnie, wbij ostrze w sąsiedni wierzchołek kwadratu i narysuj kolejny łuk, przecinający pierwszy. Punkt przecięcia łuków to wierzchołek jednego z trójkątów bocznych. Powtórz to dla każdej pary wierzchołków podstawy, aby wyznaczyć wierzchołki wszystkich czterech trójkątów. Dzięki temu wszystkie trójkątne ściany boczne będą miały ramiona o tej samej, poprawnej długości i idealnie zbiegną się w wierzchołku.
Ostrosłup prawidłowy trójkątny (czworościan): co musisz wiedzieć?
Ostrosłup prawidłowy trójkątny, czyli czworościan, to jedna z najbardziej symetrycznych brył. Jeśli jest to czworościan foremny, wszystkie jego cztery ściany są identycznymi trójkątami równobocznymi. To fascynująca bryła, która składa się wyłącznie z trójkątów!
Instrukcja rysowania siatki złożonej z czterech trójkątów równobocznych
Rysowanie siatki czworościanu foremnego jest stosunkowo proste, ponieważ wszystkie jego ściany są takie same:
- Narysuj podstawę: Narysuj jeden trójkąt równoboczny o zadanej długości boku ('a'). To będzie podstawa czworościanu.
- Dorysuj ściany boczne: Do każdego z trzech boków tego trójkąta dorysuj po jednym identycznym trójkącie równobocznym.
- Sprawdź symetrię: Po złożeniu, te trzy trójkąty boczne spotkają się w jednym wierzchołku, tworząc bryłę. Cała siatka powinna przypominać duży trójkąt równoboczny podzielony na cztery mniejsze.
Kluczem jest tutaj precyzyjne rysowanie trójkątów równobocznych za pomocą cyrkla i linijki, aby wszystkie boki były równe, a kąty miały 60 stopni.
Siatka ostrosłupa o podstawie sześciokąta: wyzwanie dla zaawansowanych
Ostrosłup o podstawie sześciokąta foremnego to już wyzwanie dla tych, którzy opanowali podstawy. Jego siatka składa się z jednej sześciokątnej podstawy i sześciu trójkątnych ścian bocznych. Tutaj precyzja jest podwójnie ważna.
Precyzyjne rysowanie podstawy i dopasowanie trójkątnych ścian
Oto jak podejść do rysowania siatki ostrosłupa o podstawie sześciokąta foremnego:
- Narysuj podstawę sześciokątną: Postępuj dokładnie tak, jak opisałem wcześniej dla graniastosłupa sześciokątnego użyj cyrkla, aby narysować idealny sześciokąt foremny o boku 'a'.
- Wyznacz krawędzie boczne: Podobnie jak w ostrosłupie czworokątnym, musisz znać długość krawędzi bocznej ostrosłupa ('k'). Otwórz cyrkiel na tę długość.
- Dorysuj ściany boczne: Wbij ostrze cyrkla w każdy z wierzchołków sześciokąta i narysuj łuki, które przetną się w punkcie będącym wierzchołkiem ostrosłupa. Połącz wierzchołki sześciokąta z tym punktem. Powstaną sześć identycznych trójkątów równoramiennych, których podstawą jest bok sześciokąta, a ramionami są krawędzie boczne ostrosłupa.
- Sprawdź zbieżność: Upewnij się, że wszystkie wierzchołki trójkątów bocznych zbiegają się w jednym punkcie. Jeśli tak, siatka jest poprawnie narysowana.
Najczęstsze błędy przy rysowaniu siatek: jak ich unikać?
Wielokrotnie widziałem, jak moi uczniowie popełniają te same błędy. To naturalne, ale warto je znać, aby świadomie ich unikać. Pamiętaj, że nauka na błędach to najszybsza droga do mistrzostwa!
Zła liczba lub kształt ścian: jak tego uniknąć?
To jeden z najczęstszych problemów. Uczniowie często gubią się w liczbie ścian bocznych lub rysują je w niewłaściwym kształcie. Na przykład, rysują cztery ściany boczne dla graniastosłupa trójkątnego albo prostokątne ściany boczne dla ostrosłupa.
- Dokładnie policz krawędzie podstawy: Liczba ścian bocznych graniastosłupa i ostrosłupa zawsze odpowiada liczbie boków podstawy. Jeśli podstawa jest trójkątem, masz trzy ściany boczne. Jeśli sześciokątem sześć.
- Pamiętaj o kształcie ścian: W graniastosłupach ściany boczne są prostokątami (lub równoległobokami). W ostrosłupach zawsze trójkątami.
- Sprawdź proporcje: Czy ściany boczne mają odpowiednie wymiary? Czy są identyczne tam, gdzie powinny być (np. w graniastosłupach i ostrosłupach prawidłowych)?
Niepasujące krawędzie: dlaczego tak ważne jest precyzyjne mierzenie?
To kolejny błąd, który potrafi zrujnować całą pracę. Nawet najmniejsze niedokładności w mierzeniu długości krawędzi sprawią, że siatka po złożeniu nie będzie pasować. Krawędzie będą się rozchodzić, a bryła nie będzie spójna. Wyobraź sobie, że próbujesz skleić pudełko, którego ścianki nie mają identycznych długości to po prostu niemożliwe!
Dlatego zawsze podkreślam: precyzja to podstawa. Używaj linijki i cyrkla z największą starannością. Mierz dwukrotnie, jeśli masz wątpliwości. Lepiej poświęcić kilka dodatkowych sekund na pomiar, niż później frustrować się niepasującą siatką.
Jak zweryfikować swój rysunek? Prosty test na poprawność siatki
Zawsze zachęcam moich uczniów do weryfikacji swoich rysunków. To prosty sposób, aby upewnić się, że siatka jest poprawna, zanim oddasz ją do oceny lub zaczniesz wycinać i składać. Oto kilka wskazówek:
- Test wizualny: Spójrz na siatkę i spróbuj wyobrazić sobie, jak by się złożyła. Czy wszystkie krawędzie znajdą swoje pary? Czy nie ma "dziur" ani nakładających się części?
- Test krawędzi: Wybierz jedną krawędź na siatce (np. bok podstawy). Zastanów się, z którą krawędzią ściany bocznej będzie się stykać po złożeniu. Czy mają tę samą długość? Powtórz to dla kilku kluczowych krawędzi.
- Test złożenia (mentalny lub fizyczny): Jeśli masz czas i możliwość, możesz delikatnie wyciąć siatkę i spróbować ją złożyć bez klejenia. To najlepszy sposób na szybką weryfikację. Jeśli wszystkie krawędzie się stykają i bryła jest zamknięta, to gratuluję siatka jest poprawna!
- Liczba ścian: Upewnij się, że liczba ścian na siatce odpowiada liczbie ścian bryły. Na przykład, sześcian ma 6 ścian, graniastosłup trójkątny 5 (2 podstawy + 3 boczne), ostrosłup czworokątny 5 (1 podstawa + 4 boczne).
Od siatki do bryły: praktyczne wskazówki i zastosowania
Dlaczego warto ćwiczyć rysowanie na papierze w kratkę?
Wspominałem już o tym wcześniej, ale powtórzę: papier w kratkę to Twój sprzymierzeniec! Dlaczego? Po pierwsze, ułatwia zachowanie prostych kątów i równoległych linii. Nie musisz za każdym razem używać ekierki do rysowania idealnie prostej ściany bocznej graniastosłupa kratki Cię poprowadzą. Po drugie, pomaga w liczeniu jednostek i zachowaniu proporcji. Jeśli krawędź ma mieć 4 cm, łatwo odliczysz 4 kratki. To znacznie przyspiesza pracę i zwiększa precyzję, co jest kluczowe, zwłaszcza na początku nauki.
Przeczytaj również: Szybkie procenty na kalkulatorze: obliczaj rabaty i VAT bez błędów
Zrozumienie siatek to nie tylko oceny z matematyki: gdzie Ci się to przyda?
Może Ci się wydawać, że rysowanie siatek to tylko kolejne zadanie z matematyki, które trzeba zaliczyć. Nic bardziej mylnego! Umiejętność wizualizacji brył w 2D i 3D ma mnóstwo praktycznych zastosowań w życiu codziennym i w różnych zawodach:
- Projektowanie opakowań: Każde pudełko, karton czy opakowanie, które widzisz w sklepie, zaczęło swoje życie jako siatka. Projektanci muszą wiedzieć, jak rozłożyć bryłę, aby stworzyć funkcjonalne i estetyczne opakowanie.
- Tworzenie modeli 3D: Jeśli interesujesz się grafiką komputerową, architekturą czy inżynierią, zrozumienie siatek jest podstawą do tworzenia trójwymiarowych modeli obiektów.
- Budownictwo i stolarstwo: Architekci i stolarze często muszą wyobrazić sobie, jak płaskie materiały (np. płyty gipsowo-kartonowe, drewno) zostaną złożone, aby stworzyć trójwymiarową konstrukcję.
- Sztuka i design: Artyści i projektanci wykorzystują zasady geometrii przestrzennej do tworzenia rzeźb, instalacji czy elementów wyposażenia wnętrz.
- Rozwój wyobraźni przestrzennej: Niezależnie od przyszłego zawodu, ćwiczenie rysowania siatek wspaniale rozwija wyobraźnię przestrzenną, co jest umiejętnością cenną w wielu dziedzinach życia.

