Zrozumienie geometrii przestrzennej, a zwłaszcza właściwości kuli, jest fundamentem w nauce matematyki, zarówno w szkole, jak i na studiach. W tym artykule, jako Igor Lis, moim celem jest dostarczenie Wam precyzyjnych wzorów na objętość i pole powierzchni kuli, a także dokładne objaśnienie ich symboli. Przejdziemy również przez praktyczne przykłady obliczeniowe krok po kroku, które pomogą Wam zastosować te wzory w praktyce i rozwiać wszelkie wątpliwości.
Kluczowe wzory na objętość i pole powierzchni kuli szybki przewodnik z przykładami
- Objętość kuli (V) obliczamy wzorem: V = (4/3)πr³, gdzie 'r' to promień.
- Pole powierzchni kuli (P) obliczamy wzorem: P = 4πr², gdzie 'r' to promień.
- Promień (r) to odległość od środka kuli do jej powierzchni; liczba Pi (π) to stała, najczęściej przyjmowana jako 3,14.
- Uważaj na średnicę (d), która jest dwukrotnością promienia (d=2r) to częste źródło błędów w zadaniach.
- Jednostki: objętość podajemy w jednostkach sześciennych (np. cm³), a pole powierzchni w jednostkach kwadratowych (np. cm²).
- W artykule znajdziesz praktyczne przykłady obliczeń krok po kroku, które pomogą Ci zastosować wzory.
Zrozumienie kuli: co to jest i dlaczego wzory są kluczowe?
Kula to jedna z najbardziej fundamentalnych i symetrycznych brył geometrycznych, którą spotykamy zarówno w matematyce, jak i w otaczającym nas świecie. W kontekście matematycznym, jej właściwości są niezwykle ważne do zrozumienia geometrii przestrzennej. Znajomość wzorów na objętość i pole powierzchni kuli jest kluczowa nie tylko dla uczniów i studentów, którzy mierzą się z zadaniami z geometrii, ale także w wielu praktycznych zastosowaniach od inżynierii po fizykę. Pozwala nam to obliczyć, ile "miejsca" zajmuje dana kula lub ile materiału potrzeba do pokrycia jej powierzchni.
Definicja kuli, czyli co odróżnia ją od sfery?
W matematyce precyzja jest niezwykle ważna, dlatego warto rozróżnić dwa często mylone pojęcia: kulę i sferę. Kula to tak naprawdę bryła obrotowa, którą można sobie wyobrazić jako obrót koła wokół jego średnicy. Jest to zbiór wszystkich punktów w przestrzeni, których odległość od stałego punktu (środka) jest nie większa niż promień. Mówiąc prościej, kula to to, co jest "w środku" i na "zewnątrz". Natomiast sfera to powierzchnia kuli. To zbiór wszystkich punktów w przestrzeni, których odległość od środka jest dokładnie równa promieniowi. W mowie potocznej często używamy tych terminów zamiennie, mówiąc np. "pole kuli", ale w matematyce poprawnie jest mówić o "polu powierzchni kuli", co technicznie oznacza pole sfery.
Gdzie w codziennym życiu spotykamy kule?
Kształt kuli jest wszechobecny w naszym otoczeniu, co sprawia, że zrozumienie jej właściwości jest bardzo intuicyjne. Oto kilka przykładów:
- Piłki sportowe: Piłka nożna, koszykowa, tenisowa wszystkie są kulami (lub bardzo zbliżonymi do kul).
- Owoce: Pomarańcze, jabłka (choć nieidealne), arbuzy.
- Bańki mydlane: Idealne kule, jeśli nie ma zewnętrznych zakłóceń.
- Krople wody: W stanie nieważkości przyjmują kształt kuli.
- Planety i gwiazdy: W skali kosmicznej, obiekty te są niemal idealnymi kulami.
- Łożyska kulkowe: Niezbędne w mechanice, pozwalają na płynny ruch.
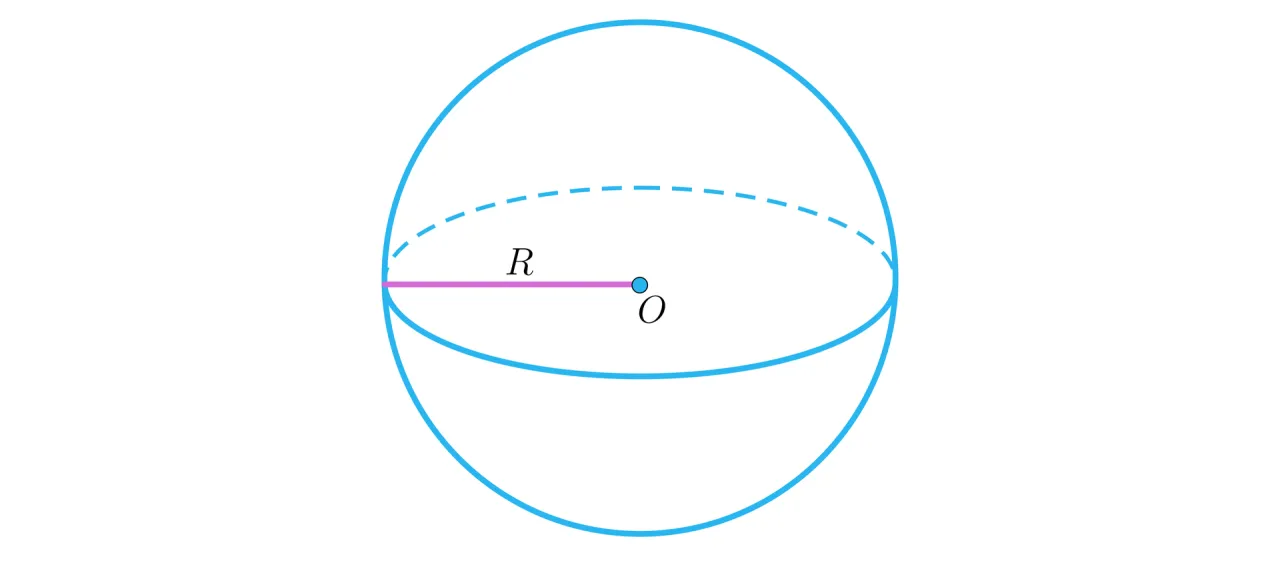
Objętość kuli: wzór, objaśnienia i praktyczne obliczenia
Objętość kuli to nic innego jak miara przestrzeni, którą ta bryła zajmuje. Wyobraź sobie, ile wody zmieściłoby się w idealnie kulistym naczyniu. To właśnie objętość! Jest to jeden z podstawowych parametrów, który musimy umieć obliczyć, pracując z kulami. Przejdźmy do konkretów.
Prezentacja kluczowego wzoru: V = (4/3)πr³
Kluczowy wzór na objętość kuli, który musisz znać, wygląda następująco:
V = (4/3)πr³
Co oznaczają poszczególne symbole we wzorze? Wyjaśnienie krok po kroku
Aby wzór był dla Ciebie w pełni zrozumiały, rozłóżmy go na czynniki pierwsze:- V: To symbol oznaczający objętość kuli. Pamiętaj, że objętość zawsze podajemy w jednostkach sześciennych, np. centymetrach sześciennych (cm³), metrach sześciennych (m³) czy litrach (gdzie 1 litr = 1 dm³).
- π (Pi): To słynna stała matematyczna, która pojawia się w wielu wzorach związanych z okręgami i kulami. Jej wartość jest nieskończonym, nieokresowym ułamkiem dziesiętnym (3,14159...). W zadaniach szkolnych najczęściej przyjmujemy jej przybliżenia: 3,14 lub, rzadziej, 22/7.
- r: To promień kuli. Promień to odległość od środka kuli do dowolnego punktu na jej powierzchni. Jest to kluczowy parametr, który musisz znać, aby obliczyć objętość. Pamiętaj, że 'r³' oznacza 'r' podniesione do potęgi trzeciej, czyli r * r * r.
Obliczamy objętość kuli w praktyce: zadanie z rozwiązaniem
Wyobraź sobie, że masz kulę o promieniu r = 3 cm. Obliczmy jej objętość:
- Zapisz wzór: V = (4/3)πr³
- Podstaw dane: W naszym przypadku r = 3 cm. Przyjmijmy π ≈ 3,14. V = (4/3) * 3,14 * (3 cm)³
- Oblicz potęgę: (3 cm)³ = 3 cm * 3 cm * 3 cm = 27 cm³
- Podstaw wynik do wzoru: V = (4/3) * 3,14 * 27 cm³
- Wykonaj mnożenie: V = (4 * 27 / 3) * 3,14 cm³ V = (108 / 3) * 3,14 cm³ V = 36 * 3,14 cm³
- Oblicz końcowy wynik: V = 113,04 cm³
Zatem objętość kuli o promieniu 3 cm wynosi około 113,04 cm³.
Pole powierzchni kuli: wzór i zastosowanie
Poza objętością, często musimy obliczyć również pole powierzchni kuli. Pomyśl o tym jako o ilości materiału potrzebnego do pokrycia całej zewnętrznej warstwy kuli, na przykład farby do pomalowania piłki. To również bardzo praktyczna umiejętność.
Oto wzór, którego szukasz: P = 4πr²
Wzór na pole powierzchni kuli jest równie elegancki i prosty:
P = 4πr²
Dekodujemy wzór na pole: rola promienia i liczby π
Podobnie jak przy objętości, rozłóżmy ten wzór na części:
- P: Oznacza pole powierzchni kuli. Jednostką pola powierzchni są zawsze jednostki kwadratowe, np. centymetry kwadratowe (cm²), metry kwadratowe (m²).
- π (Pi): Ponownie, nasza stała matematyczna, której przybliżenie to 3,14.
- r: To promień kuli. W tym wzorze promień jest podniesiony do potęgi drugiej (r²), co oznacza r * r.
Zauważ, że wzór na pole powierzchni kuli jest bardzo podobny do wzoru na pole koła (πr²), ale pomnożony przez 4. To pokazuje, jak cztery koła o tym samym promieniu co kula, mogłyby pokryć jej powierzchnię.
Jak obliczyć pole powierzchni kuli? Konkretny przykład
Kontynuując nasz przykład, obliczmy pole powierzchni tej samej kuli o promieniu r = 3 cm:
- Zapisz wzór: P = 4πr²
- Podstaw dane: r = 3 cm. Przyjmijmy π ≈ 3,14. P = 4 * 3,14 * (3 cm)²
- Oblicz potęgę: (3 cm)² = 3 cm * 3 cm = 9 cm²
- Podstaw wynik do wzoru: P = 4 * 3,14 * 9 cm²
- Wykonaj mnożenie: P = 12,56 * 9 cm²
- Oblicz końcowy wynik: P = 113,04 cm²
Pole powierzchni kuli o promieniu 3 cm wynosi około 113,04 cm². Zwróć uwagę, że w tym konkretnym przypadku (dla r=3) wartość liczbowa objętości i pola powierzchni jest taka sama, ale jednostki są różne (cm³ vs cm²)! To tylko zbieg okoliczności dla tej konkretnej wartości promienia.
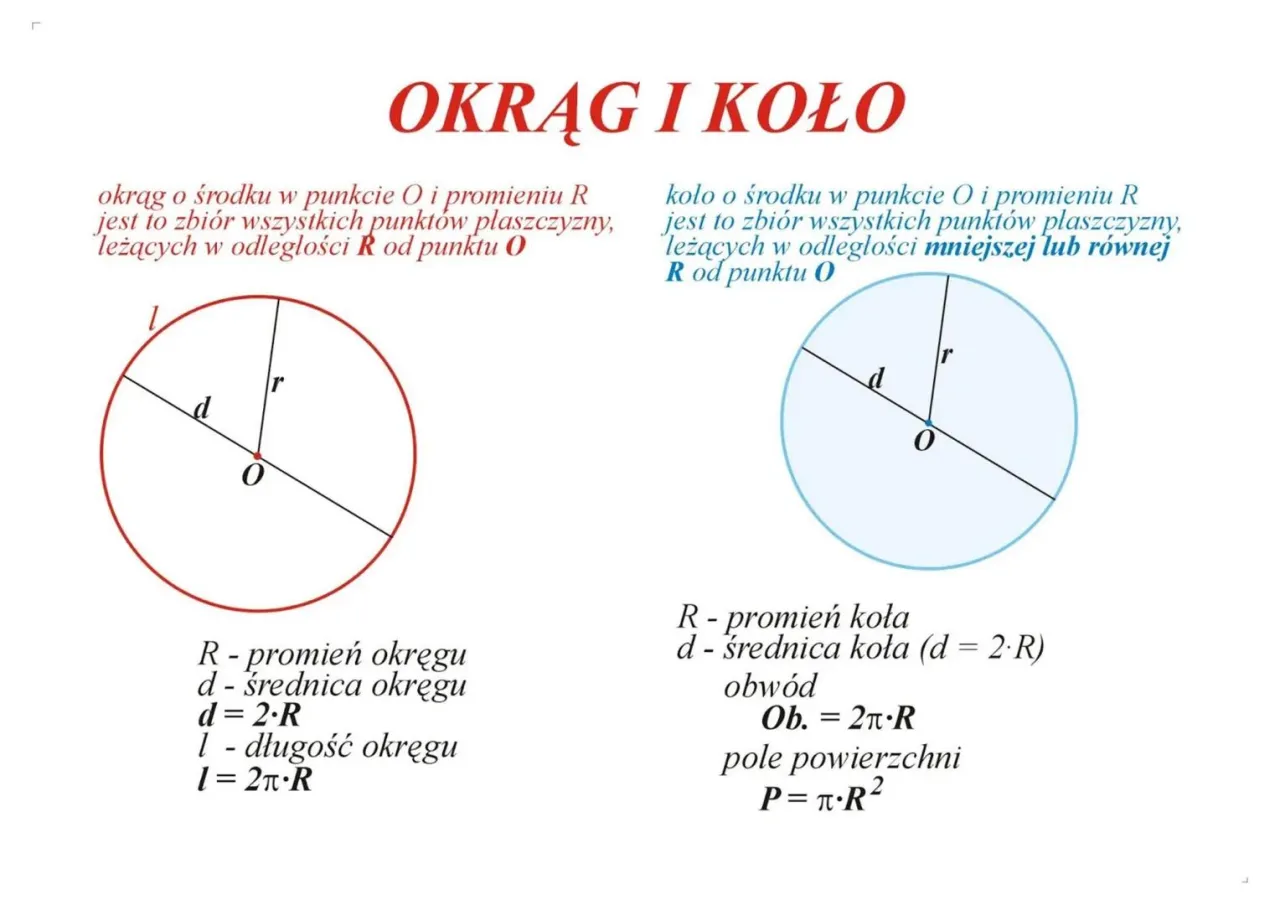
Unikaj pułapek: promień a średnica
Jednym z najczęstszych błędów, jakie widzę u uczniów, jest mylenie promienia ze średnicą. To prosta pomyłka, która jednak prowadzi do całkowicie błędnych wyników. Musimy być bardzo ostrożni i zawsze sprawdzać, czy w zadaniu podano promień, czy średnicę.Mając średnicę, a nie promień jak poprawnie wykonać obliczenia?
Pamiętaj, że średnica (d) kuli to odcinek łączący dwa punkty na jej powierzchni i przechodzący przez jej środek. Promień (r) to natomiast odległość od środka do powierzchni. Z tego wynika bardzo prosta zależność: średnica jest zawsze dwukrotnością promienia (d = 2r). Co za tym idzie, promień to połowa średnicy (r = d/2). Jeśli w zadaniu podana jest średnica, pierwszym krokiem zawsze musi być obliczenie promienia!
Zadanie-pułapka: oblicz objętość i pole kuli o podanej średnicy
Załóżmy, że mamy kulę o średnicy d = 6 cm. Obliczmy jej objętość i pole powierzchni.
- Krok kluczowy: Oblicz promień! Skoro d = 6 cm, to r = d/2 = 6 cm / 2 = 3 cm.
-
Oblicz objętość (V):
- Wzór: V = (4/3)πr³
- Podstawiamy r = 3 cm (zwróć uwagę, że to ten sam promień co w poprzednich przykładach!): V = (4/3) * 3,14 * (3 cm)³
- Obliczamy: V = (4/3) * 3,14 * 27 cm³ = 36 * 3,14 cm³ = 113,04 cm³
-
Oblicz pole powierzchni (P):
- Wzór: P = 4πr²
- Podstawiamy r = 3 cm: P = 4 * 3,14 * (3 cm)²
- Obliczamy: P = 4 * 3,14 * 9 cm² = 113,04 cm²
Jak widzisz, kluczowe było prawidłowe przekształcenie średnicy na promień na samym początku. Bez tego, wszystkie dalsze obliczenia byłyby błędne.
Przekształcanie wzorów: od objętości do pola
W bardziej zaawansowanych zadaniach często zdarza się, że nie mamy podanego promienia wprost. Zamiast tego, znamy objętość kuli i musimy z niej wyznaczyć promień, aby następnie obliczyć pole powierzchni. To świetny trening umiejętności algebraicznych!
Jak wyliczyć promień kuli, znając jej objętość?
Przyjmijmy, że znamy objętość kuli (V) i chcemy wyznaczyć promień (r). Musimy przekształcić wzór V = (4/3)πr³:
- Zapisz wzór: V = (4/3)πr³
- Pomnóż obie strony przez 3, aby pozbyć się ułamka: 3V = 4πr³
- Podziel obie strony przez 4π, aby wyizolować r³: r³ = 3V / (4π)
- Aby pozbyć się potęgi trzeciej, wyciągnij pierwiastek sześcienny z obu stron: r = ∛(3V / (4π))
I oto mamy wzór na promień kuli, znając jej objętość! To pokazuje, jak elastyczne są wzory matematyczne.
Zadanie dla ambitnych: oblicz pole powierzchni, mając tylko objętość
Masz kulę, której objętość wynosi V = 36π cm³. Oblicz jej pole powierzchni.
-
Krok 1: Oblicz promień kuli z objętości.
- Wzór na objętość: V = (4/3)πr³
- Podstawiamy znaną objętość: 36π = (4/3)πr³
- Podziel obie strony przez π (możemy to zrobić, bo π ≠ 0): 36 = (4/3)r³
- Pomnóż obie strony przez 3: 3 * 36 = 4r³ 108 = 4r³
- Podziel obie strony przez 4: 108 / 4 = r³ 27 = r³
- Wyciągnij pierwiastek sześcienny z obu stron: r = ∛27 r = 3 cm
-
Krok 2: Oblicz pole powierzchni, używając wyznaczonego promienia.
- Wzór na pole powierzchni: P = 4πr²
- Podstawiamy r = 3 cm: P = 4 * π * (3 cm)²
- Obliczamy: P = 4 * π * 9 cm² P = 36π cm²
Zatem kula o objętości 36π cm³ ma pole powierzchni równe 36π cm². Zauważ, że w tym przypadku zostawiłem π w wyniku, co jest często akceptowalne, a nawet preferowane w matematyce, jeśli nie jest wymagane przybliżenie.

Wzory na kulę w praktyce: przyklady z życia
Matematyka nie jest oderwana od rzeczywistości. Wzory na objętość i pole powierzchni kuli mają swoje realne zastosowania. Przyjrzyjmy się kilku przykładom, które pokazują, jak ta wiedza przydaje się w codziennym życiu.
Ile powietrza zmieści się w piłce? Obliczenia z życia wzięte
Weźmy standardową piłkę nożną, która ma promień około 11 cm. Ile powietrza (czyli jaką objętość) musimy do niej wtłoczyć, aby była odpowiednio napompowana? Użyjemy wzoru na objętość kuli: V = (4/3)πr³. Przyjmijmy π ≈ 3,14 i r = 11 cm. V = (4/3) * 3,14 * (11 cm)³ V = (4/3) * 3,14 * 1331 cm³ V = 5572,453... cm³ V ≈ 5572,45 cm³.
To oznacza, że w takiej piłce zmieści się około 5,57 litra powietrza (ponieważ 1 litr = 1000 cm³). Dzięki temu prostemu obliczeniu możemy zrozumieć, ile gazu potrzebujemy do napełnienia kulistego zbiornika lub ile płynu zmieści się w kulistej butelce.
Przeczytaj również: Silnia (n!): Jak uporządkować świat? Kombinatoryka bez tajemnic
Jak zmieni się objętość kuli, gdy podwoimy jej promień? Efekt skali w praktyce
To bardzo ciekawe zagadnienie, które pokazuje, jak potęgi wpływają na wyniki. Zastanówmy się, co się stanie z objętością kuli, jeśli podwoimy jej promień. Niech początkowy promień wynosi r. Wtedy objętość to V₁ = (4/3)πr³. Jeśli podwoimy promień, nowy promień będzie wynosił 2r. Wtedy nowa objętość to V₂ = (4/3)π(2r)³. V₂ = (4/3)π(8r³) V₂ = 8 * (4/3)πr³ V₂ = 8 * V₁
Jak widać, podwojenie promienia kuli powoduje ośmiokrotny wzrost jej objętości! To efekt skali, który wynika z potęgi trzeciej w wzorze na objętość. Jeśli promień wzrósłby trzykrotnie, objętość wzrosłaby 3³ = 27 razy. To ważna zasada, którą warto zapamiętać, ponieważ ma zastosowanie w wielu dziedzinach, od projektowania zbiorników po zrozumienie wzrostu organizmów.

