Witaj w przewodniku, który ma na celu ułatwić Ci zrozumienie i zapamiętanie kluczowych wartości funkcji trygonometrycznych sinusa i cosinusa. Jako ktoś, kto spędził lata na zgłębianiu matematyki i pomaganiu innym w jej opanowaniu, wiem, jak ważne jest solidne opanowanie tych podstaw. Ten artykuł to Twój niezbędnik, który pomoże Ci nie tylko w nauce do sprawdzianów czy egzaminu maturalnego, ale także zbuduje solidne fundamenty do dalszej przygody z trygonometrią i jej praktycznymi zastosowaniami.
Kompletna tabela wartości sinusa i cosinusa Twój przewodnik po trygonometrii
- Kluczowe wartości dla kątów 0°, 30°, 45°, 60° i 90° są fundamentem trygonometrii i niezbędne na egzaminach.
- Tabele trygonometryczne przedstawiają wartości dla kątów w stopniach i radianach.
- Wzory redukcyjne umożliwiają obliczanie wartości funkcji dla kątów większych niż 90°.
- Zrozumienie znaków funkcji w poszczególnych ćwiartkach układu współrzędnych jest kluczowe przy redukcji.
- Znajomość wartości sinusa i cosinusa ma szerokie zastosowanie w wielu praktycznych dziedzinach, od geodezji po grafikę komputerową.
Dlaczego tabela wartości trygonometrycznych to niezbędnik każdego ucznia?
Dla każdego ucznia, zwłaszcza tego, który przygotowuje się do egzaminu maturalnego, znajomość wartości funkcji trygonometrycznych jest absolutnie kluczowa. Sinus i cosinus to fundament, na którym opiera się cała trygonometria, a bez zrozumienia ich podstawowych wartości trudno jest ruszyć dalej. W mojej praktyce często widzę, jak uczniowie zmagają się z zadaniami, które wymagają szybkiego i precyzyjnego odczytania lub przypomnienia sobie tych liczb.
Historycznie, tablice trygonometryczne były jedynym sposobem na wykonywanie skomplikowanych obliczeń w nawigacji, astronomii czy inżynierii. Dziś, choć mamy kalkulatory, zrozumienie i pamięć kluczowych wartości pozostaje niezastąpione. Pozwala to nie tylko na szybkie rozwiązywanie zadań, ale także na głębsze zrozumienie zależności geometrycznych i fizycznych. To wiedza, która procentuje!
Wartości, które musisz znać na pamięć: tabela dla kątów charakterystycznych
Istnieje zestaw wartości, które każdy uczeń powinien znać niemal na pamięć. To tak zwane kąty charakterystyczne, które pojawiają się w zadaniach egzaminacyjnych niezwykle często. Poniższa tabela przedstawia te kluczowe wartości dla sinusa i cosinusa, zarówno w stopniach, jak i radianach.
| Kąt (stopnie) | Kąt (radiany) | sin(α) | cos(α) |
|---|---|---|---|
| 0° | 0 | 0 | 1 |
| 30° | π/6 | 1/2 | √3/2 |
| 45° | π/4 | √2/2 | √2/2 |
| 60° | π/3 | √3/2 | 1/2 |
| 90° | π/2 | 1 | 0 |
Aby ułatwić sobie zapamiętanie tych wartości, polecam prosty trik, często nazywany "metodą dłoni" lub "palców". Wyobraź sobie swoją lewą dłoń rozłożoną. Palce oznaczają kąty: kciuk to 0°, wskazujący 30°, środkowy 45°, serdeczny 60°, a mały palec 90°. Aby znaleźć wartość sinusa dla danego kąta, zegnij odpowiedni palec. Następnie policz palce poniżej zgiętego palca, spierwiastkuj tę liczbę i podziel przez 2. Na przykład dla 30° (palec wskazujący) masz jeden palec poniżej (kciuk), więc √1/2 = 1/2. Dla cosinusa robisz to samo, ale liczysz palce powyżej zgiętego palca. Spróbuj, to naprawdę działa i pomaga w kryzysowych sytuacjach!
Jak poprawnie odczytać wartości sinusa i cosinusa z pełnej tabeli? Instrukcja krok po kroku
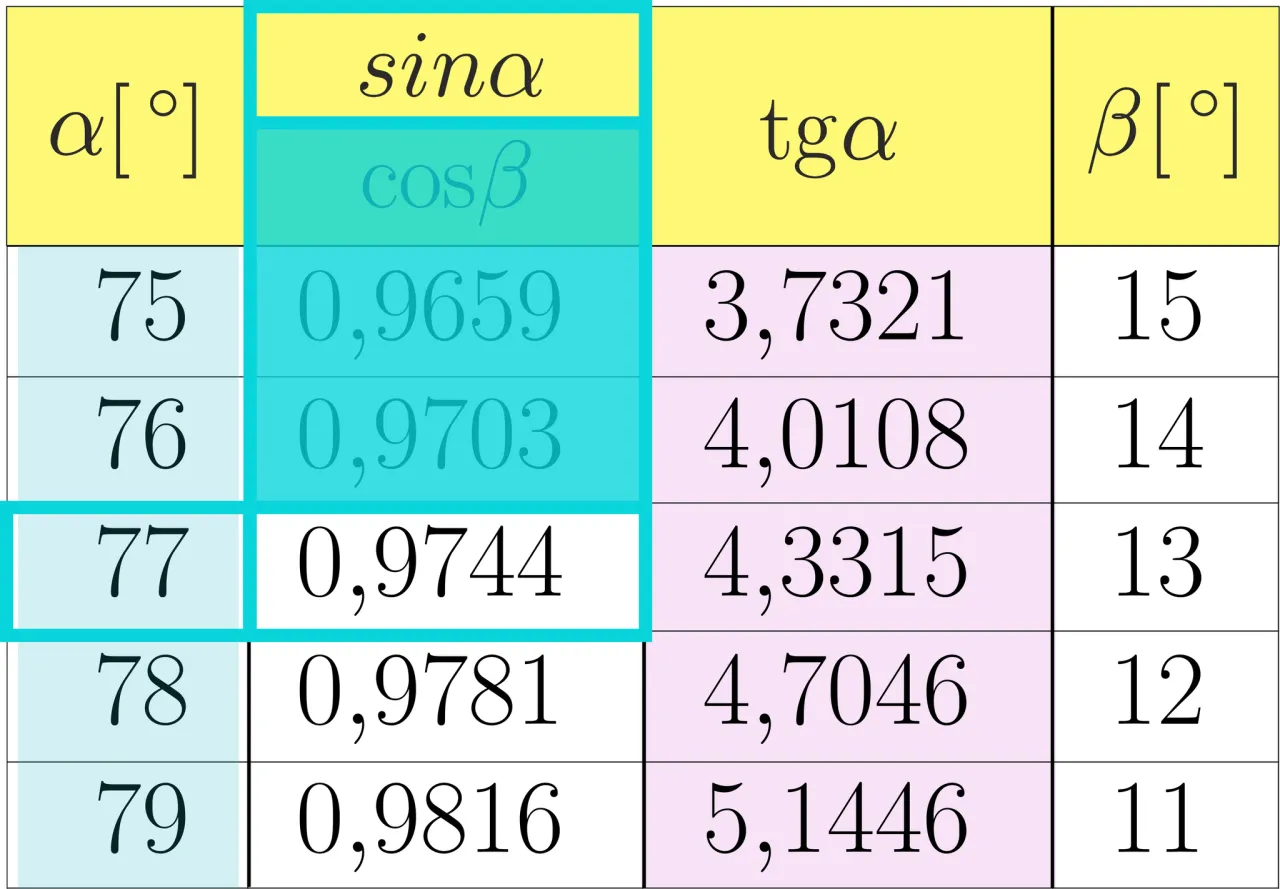
Oprócz kątów charakterystycznych, które warto znać na pamięć, często potrzebujemy wartości dla innych kątów ostrych. W tym celu korzystamy z pełnych tablic trygonometrycznych, takich jak te dostępne w oficjalnych materiałach CKE na egzamin maturalny. Odczytywanie z nich jest proste, jeśli znasz podstawowe zasady:
- Zlokalizuj miarę kąta: Zazwyczaj w pierwszej kolumnie tabeli (lub w pierwszym wierszu, w zależności od układu) znajdziesz miary kątów, najczęściej wyrażone w stopniach (od 0° do 90°). Upewnij się, że patrzysz na właściwą jednostkę, jeśli tabela zawiera również radiany.
- Wybierz odpowiednią funkcję: Znajdź kolumnę lub wiersz odpowiadający funkcji, której wartość chcesz odczytać w naszym przypadku będzie to "sin(α)" lub "cos(α)". Nagłówki tabel są zazwyczaj bardzo czytelne.
- Przecięcie wiersza i kolumny: Przejdź wzdłuż wiersza z wybranym kątem, aż do kolumny z wybraną funkcją. Wartość znajdująca się na ich przecięciu to szukana wartość funkcji dla danego kąta.
- Zwróć uwagę na precyzję: W tablicach maturalnych wartości są zazwyczaj podawane z dokładnością do czterech miejsc po przecinku. Pamiętaj, że są to wartości przybliżone, a nie zawsze dokładne.
Wartości w tablicach są często przybliżone, ponieważ wiele funkcji trygonometrycznych dla kątów innych niż charakterystyczne daje liczby niewymierne. Na przykład sin(1°) to nieskończony ułamek dziesiętny, który dla celów praktycznych zaokrągla się do określonej liczby miejsc po przecinku. To ważne, aby pamiętać o tym w obliczeniach, zwłaszcza gdy wymagana jest wysoka precyzja, choć w szkole średniej zazwyczaj akceptowane są te zaokrąglone wartości.
Kąty większe niż 90°: jak wzory redukcyjne rozszerzają możliwości tabeli
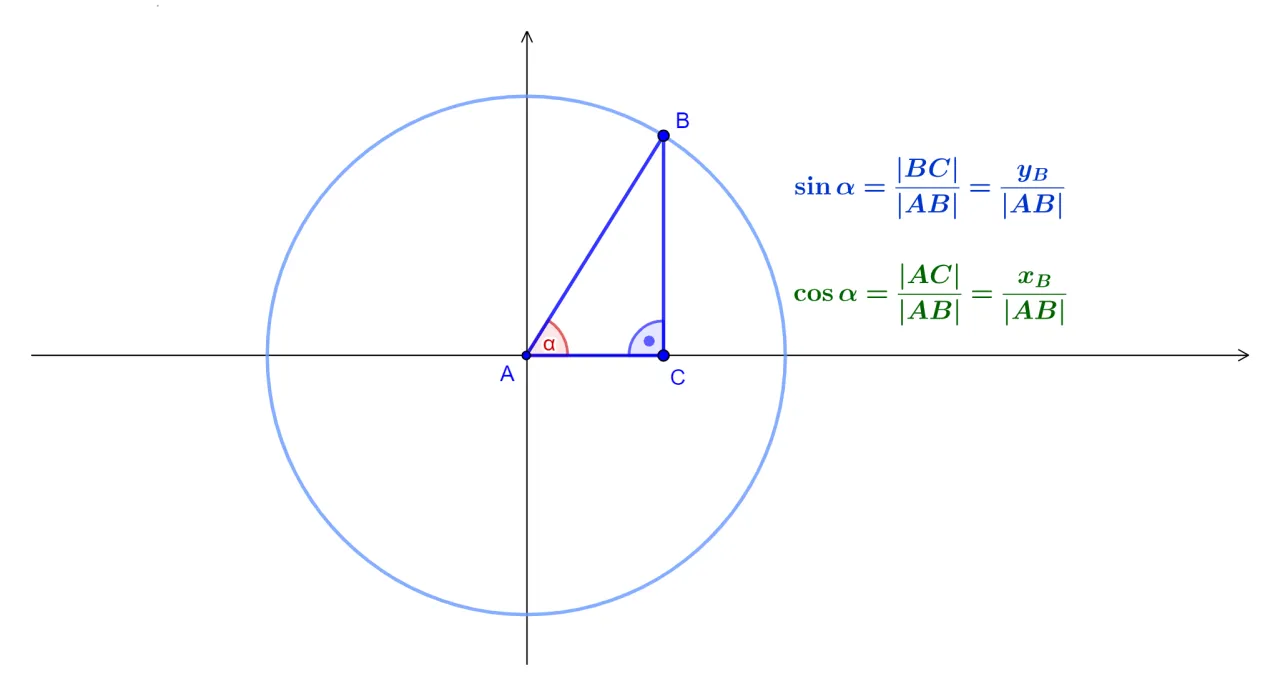
Co zrobić, gdy potrzebujemy wartości sinusa lub cosinusa dla kąta większego niż 90°? Tutaj z pomocą przychodzą wzory redukcyjne, które pozwalają sprowadzić obliczenia do kątów ostrych (0°-90°). Kluczem do ich zrozumienia jest znajomość układu współrzędnych i tzw. ćwiartek.
Okrąg jednostkowy dzieli płaszczyznę na cztery ćwiartki:
- I ćwiartka (0° do 90°): Wszystkie funkcje trygonometryczne (sinus, cosinus, tangens, cotangens) są dodatnie.
- II ćwiartka (90° do 180°): Tylko sinus jest dodatni. Cosinus, tangens i cotangens są ujemne.
- III ćwiartka (180° do 270°): Tylko tangens i cotangens są dodatnie. Sinus i cosinus są ujemne.
- IV ćwiartka (270° do 360°): Tylko cosinus jest dodatni. Sinus, tangens i cotangens są ujemne.
Aby zapamiętać znaki funkcji w poszczególnych ćwiartkach, wielu uczniów korzysta z prostej rymowanki: "W pierwszej wszystkie są dodatnie, w drugiej tylko sinus, w trzeciej tangens i cotangens, a w czwartej cosinus." To niezwykle pomocne narzędzie!
Zobaczmy, jak to działa w praktyce:
-
Obliczanie sin(120°): Kąt 120° leży w II ćwiartce. W II ćwiartce sinus jest dodatni. Możemy zapisać 120° jako 180° - 60° lub 90° + 30°. Używając wzoru redukcyjnego dla 180°: sin(180° - α) = sin(α). Zatem sin(120°) = sin(180° - 60°) = sin(60°) = √3/2.
-
Obliczanie cos(225°): Kąt 225° leży w III ćwiartce. W III ćwiartce cosinus jest ujemny. Możemy zapisać 225° jako 180° + 45°. Używając wzoru redukcyjnego dla 180°: cos(180° + α) = -cos(α). Zatem cos(225°) = cos(180° + 45°) = -cos(45°) = -√2/2.
Warto również pamiętać, że w niektórych wzorach redukcyjnych (gdy kąt jest typu 90° ± α lub 270° ± α) funkcja zmienia się w tzw. kofunkcję. Oznacza to, że sinus staje się cosinusem, a cosinus sinusem. Na przykład sin(90° + α) = cos(α) lub cos(270° - α) = -sin(α). Zawsze jednak musimy pamiętać o prawidłowym znaku funkcji w danej ćwiartce, zanim zastosujemy zamianę na kofunkcję.
Najczęstsze pułapki i błędy: na co uważać podczas pracy z tabelą wartości
Nawet doświadczeni uczniowie potrafią popełniać błędy, zwłaszcza pod presją czasu. Oto najczęstsze pułapki, na które musisz uważać:
-
Mylenie kolumn sinusa i cosinusa: To zdarza się częściej, niż myślisz! W pośpiechu łatwo pomylić kolumny w tabeli. Zawsze upewnij się, że odczytujesz wartość z właściwej funkcji. Podobnie, podczas zapamiętywania kątów charakterystycznych, upewnij się, że przypisujesz odpowiednią wartość do sinusa i cosinusa.
-
Błędne stosowanie znaków przy redukcji: To chyba największy "zabójca" punktów w zadaniach z trygonometrii. Zapomnienie o zasadach znaków w poszczególnych ćwiartkach (tej rymowance!) prowadzi do całkowicie błędnych wyników. Zawsze najpierw określ ćwiartkę i znak funkcji, a dopiero potem zastosuj wzór redukcyjny.
-
Zapominanie o przeliczaniu kątów między stopniami a radianami: Niektóre zadania podają kąty w radianach, inne w stopniach. Tabele również mogą zawierać obie miary. Upewnij się, że pracujesz z właściwą jednostką lub dokonaj konwersji, jeśli to konieczne (pamiętaj, że π radianów to 180°).
Od teorii do praktyki: gdzie w realnym świecie wykorzystasz wartości sinusa i cosinusa
Może się wydawać, że sinus i cosinus to tylko abstrakcyjne pojęcia ze szkolnej ławki. Nic bardziej mylnego! Wartości tych funkcji mają ogromne znaczenie w wielu praktycznych dziedzinach, otaczających nas każdego dnia. Pozwól, że pokażę Ci kilka przykładów:
-
Geodezja i budownictwo: Geodeci wykorzystują trygonometrię do precyzyjnego mierzenia odległości, wysokości i kątów na powierzchni Ziemi. Dzięki sinusowi i cosinusowi mogą obliczyć nachylenie terenu, wysokość budynków czy wyznaczyć granice działek. Architekci i inżynierowie budowlani używają ich do projektowania konstrukcji dachów, mostów czy dróg, zapewniając ich stabilność i bezpieczeństwo.
-
Fizyka i inżynieria: W fizyce wartości sinusa i cosinusa są niezbędne do opisywania zjawisk falowych od fal dźwiękowych, przez fale świetlne, po drgania mechaniczne. Inżynierowie elektrycy wykorzystują je do analizy prądu zmiennego, a inżynierowie mechanicy do projektowania maszyn z ruchomymi elementami, takimi jak wahadła czy tłoki.
-
Grafika komputerowa i gry: Każda gra komputerowa czy animacja 3D to festiwal trygonometrii! Sinus i cosinus są używane do obracania obiektów, obliczania pozycji kamer, symulowania ruchu postaci czy generowania realistycznych efektów świetlnych i cieni. Bez nich światy wirtualne po prostu by nie istniały.

