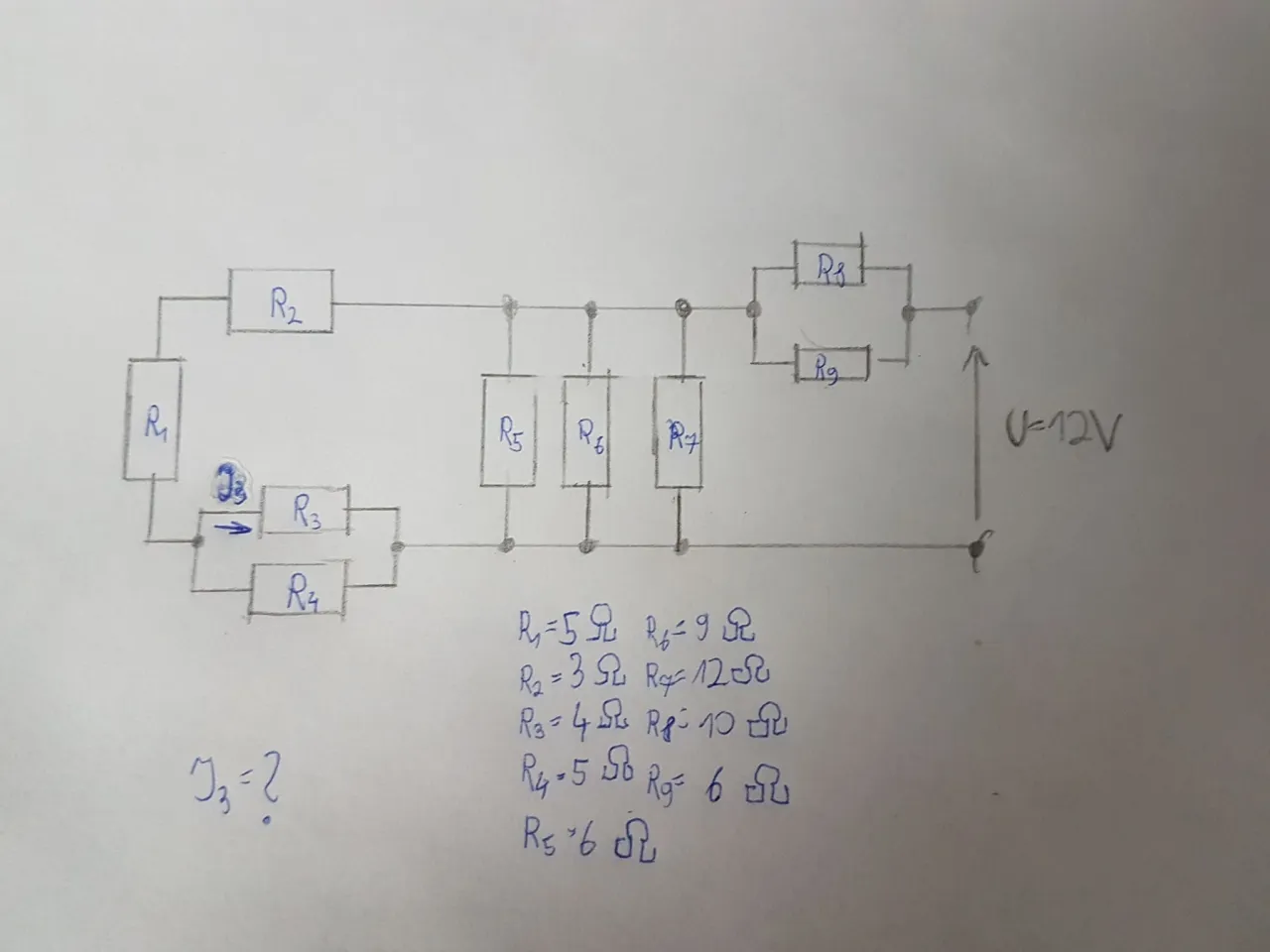
Opanuj obliczanie oporu zastępczego w trudnych obwodach: Δ-Y, Kirchhoff

Dlaczego podstawowe metody to za mało?

Zaczynając przygodę z elektroniką, szybko uczymy się, jak upraszczać obwody, łącząc rezystory szeregowo i równolegle. To podstawa, ale szybko natrafiamy na układy, które opierają się tym prostym zabiegom. Mówię tu o "trudnych" obwodach takich, w których nie jesteśmy w stanie zidentyfikować żadnych par rezystorów połączonych czysto szeregowo lub równolegle, które moglibyśmy od razu zastąpić jednym oporem zastępczym. Typowym przykładem jest mostek Wheatstone'a, zwłaszcza w wersji niezrównoważonej, gdzie rezystory tworzą zamkniętą pętlę, uniemożliwiając proste uproszczenia. Inne układy mieszane, z wieloma gałęziami i węzłami, również potrafią sprawić kłopot.

Cechy "trudnego" obwodu:

• Brak prostych połączeń: Nie ma oczywistych par rezystorów połączonych szeregowo lub równolegle.
• Złożona topologia: Obwód zawiera zamknięte pętle, mostki lub wiele rozgałęzień.
• Wielokrotne ścieżki prądu: Prąd ma wiele alternatywnych dróg przepływu, które wzajemnie na siebie oddziałują.

Właśnie w takich sytuacjach musimy sięgnąć po bardziej zaawansowane techniki, które pozwolą nam rozwikłać tę elektryczną plątaninę.

Fundamenty elektrotechniki przypomnienie

Zanim zagłębimy się w bardziej skomplikowane metody, warto na chwilę wrócić do podstaw. Nawet w najbardziej złożonych obwodach, fundamentalne prawa elektrotechniki pozostają niezmienne i stanowią podstawę do ich analizy. Zrozumienie ich to klucz do sukcesu.

Prawo Ohma Twój niezawodny towarzysz

Prawo Ohma, czyli słynne U = I * R, jest absolutną podstawą każdej analizy obwodów. Mówi nam, że napięcie (U) na rezystorze jest wprost proporcjonalne do prądu (I) płynącego przez niego i jego oporu (R). Niezależnie od tego, jak skomplikowany jest obwód, to prawo zawsze będzie obowiązywać dla każdego pojedynczego elementu rezystancyjnego. W praktyce oznacza to, że jeśli znasz dwie z tych wartości, zawsze możesz obliczyć trzecią. To nieocenione narzędzie, które będziemy wykorzystywać na każdym kroku, nawet przy stosowaniu zaawansowanych metod.

Prawa Kirchhoffa klucz do złożoności

Prawa Kirchhoffa to potężne narzędzia, które pozwalają nam analizować przepływ prądu i rozkład napięć w dowolnym obwodzie, niezależnie od jego złożoności. Są one podstawą do tworzenia układów równań, które następnie rozwiązujemy, aby znaleźć nieznane wartości.

Pierwsze Prawo Kirchhoffa (KCL) Prawo Prądowe:

• Mówi, że suma prądów wpływających do węzła jest równa sumie prądów wypływających z tego węzła.
• Innymi słowy, prąd nie może się nigdzie "zgubić" ani "pojawić znikąd" w węźle. To zasada zachowania ładunku.
• Jest to kluczowe do tworzenia równań dla węzłów w obwodzie.

Drugie Prawo Kirchhoffa (KVL) Prawo Napięciowe:

• Stwierdza, że w dowolnym zamkniętym oczku obwodu suma spadków napięć na elementach jest równa sumie sił elektromotorycznych (źródeł napięcia) w tym oczku.
• Oznacza to, że jeśli "obejdziemy" zamkniętą pętlę w obwodzie, suma wzrostów i spadków napięć musi wynosić zero. To zasada zachowania energii.
• Służy do tworzenia równań dla oczek (pętli) w obwodzie.

Te dwa prawa, choć proste w swojej idei, pozwalają na systematyczną analizę nawet najbardziej rozbudowanych układów, prowadząc do układów równań, które możemy rozwiązać.

Transformacja trójkąt-gwiazda (Δ-Y) ratunek dla mostków

Kiedy podstawowe upraszczanie zawodzi, a obwód ma strukturę mostkową lub podobną, transformacja trójkąt-gwiazda (Δ-Y) jest często pierwszym i najskuteczniejszym narzędziem, po które sięgam. Pozwala ona przekształcić fragment obwodu w inną, równoważną konfigurację, która jest łatwiejsza do dalszego uproszczenia metodami szeregowo-równoległymi.

Kluczem do zastosowania tej metody jest umiejętność wizualnego rozpoznania układów trójkąta (Δ) i gwiazdy (Y) w złożonym schemacie. Układ trójkąta (nazywany też pi lub delta) to trzy rezystory połączone ze sobą w zamkniętą pętlę, tworząc kształt trójkąta, z trzema punktami połączeń (węzłami) dostępnymi na zewnątrz. Natomiast układ gwiazdy (nazywany też T lub Y) to trzy rezystory połączone jednym końcem w wspólnym punkcie (węźle centralnym), a ich drugie końce są dostępne na zewnątrz. Często w obwodach mostkowych jeden z fragmentów (np. trzy rezystory tworzące górną część mostka lub trzy rezystory połączone wokół środkowego punktu) można zidentyfikować jako trójkąt lub gwiazdę.

Wzory na przekształcenie Δ-Y

Przekształcenie z trójkąta na gwiazdę polega na zastąpieniu trzech rezystorów połączonych w trójkąt trzema rezystorami połączonymi w gwiazdę, tak aby zachować te same właściwości elektryczne obwodu widziane z zewnątrz. Oto wzory, które są do tego potrzebne:

• R1 = (Ra * Rc) / (Ra + Rb + Rc)
  • R1 to rezystor gwiazdy połączony z węzłem, do którego w trójkącie dochodziły rezystory Ra i Rc.
  • Ra, Rb, Rc to rezystory układu trójkąta.
• R2 = (Ra * Rb) / (Ra + Rb + Rc)
  • R2 to rezystor gwiazdy połączony z węzłem, do którego w trójkącie dochodziły rezystory Ra i Rb.
  • Ra, Rb, Rc to rezystory układu trójkąta.
• R3 = (Rb * Rc) / (Ra + Rb + Rc)
  • R3 to rezystor gwiazdy połączony z węzłem, do którego w trójkącie dochodziły rezystory Rb i Rc.
  • Ra, Rb, Rc to rezystory układu trójkąta.

Przykład: Rozwiązanie niezrównoważonego mostka Wheatstone'a

Wyobraźmy sobie klasyczny, niezrównoważony mostek Wheatstone'a. Ma on cztery rezystory w ramionach i jeden rezystor łączący środkowe punkty. Nie da się go uprościć szeregowo-równolegle. Zastosujmy transformację Δ-Y:

1. Identyfikacja trójkąta: W mostku Wheatstone'a możemy zidentyfikować kilka trójkątów. Wybierzmy na przykład górny trójkąt utworzony przez rezystory R1, R2 i R5 (rezystor łączący środkowe punkty). Oznaczmy je jako Ra=R1, Rb=R2, Rc=R5.

2. Zastosowanie wzorów Δ-Y: Użyjmy wzorów, aby przekształcić ten trójkąt na gwiazdę. Obliczymy R1', R2' i R3' (nowe rezystory gwiazdy).

   • R1' = (R1 * R5) / (R1 + R2 + R5)
   • R2' = (R1 * R2) / (R1 + R2 + R5)
   • R3' = (R2 * R5) / (R1 + R2 + R5)

3. Przerysowanie obwodu: Po przekształceniu trójkąta na gwiazdę, przerysuj obwód. Zamiast rezystorów R1, R2 i R5, pojawią się rezystory R1', R2', R3' połączone w gwiazdę. Jeden koniec R1' będzie połączony z punktem, gdzie był R1 i R5, R2' z punktem, gdzie był R1 i R2, a R3' z punktem, gdzie był R2 i R5. Centralny punkt gwiazdy będzie nowym węzłem.

4. Uproszczenie obwodu: Teraz zobaczysz, że obwód stał się znacznie prostszy. Rezystor R1' będzie szeregowo z R3 (dolnym rezystorem lewego ramienia mostka), a R2' szeregowo z R4 (dolnym rezystorem prawego ramienia mostka). Te dwie gałęzie połączone szeregowo będą następnie równoległe do siebie. Na koniec, cały ten blok będzie szeregowo z R3' (rezystorem gwiazdy wychodzącym z centralnego węzła gwiazdy).

5. Obliczenie oporu zastępczego: Teraz możesz krok po kroku obliczyć opór zastępczy, stosując standardowe wzory na połączenia szeregowe i równoległe.

Unikaj pułapek najczęstsze błędy w transformacji Δ-Y

Transformacja Δ-Y jest potężna, ale łatwo o błędy. Oto, na co warto zwrócić uwagę:

• Błędne rozpoznanie układu: Upewnij się, że faktycznie masz do czynienia z trójkątem lub gwiazdą, którą można przekształcić. Czasem układ tylko przypomina te konfiguracje.
• Pomyłki algebraiczne: Wzory zawierają ułamki i sumy. Łatwo o błąd w obliczeniach, zwłaszcza przy długich szeregach działań. Sprawdzaj swoje obliczenia dwukrotnie!
• Niewłaściwe przypisanie rezystorów: Upewnij się, że rezystory Ra, Rb, Rc w trójkącie odpowiadają prawidłowym rezystorom R1, R2, R3 w gwieździe. Pamiętaj, że każdy rezystor gwiazdy jest połączony z dwoma konkretnymi rezystorami trójkąta.
• Błędy w przerysowywaniu obwodu: Po transformacji zawsze przerysuj obwód. To pomaga wizualnie ocenić nową strukturę i uniknąć błędów w dalszym upraszczaniu.

Prawa Kirchhoffa uniwersalne narzędzie do każdego obwodu

Jeśli transformacja Δ-Y nie pasuje lub obwód jest tak skomplikowany, że nie widać w nim wyraźnych struktur do przekształcenia, wtedy Prawa Kirchhoffa stają się Twoim uniwersalnym narzędziem. Pozwalają one rozwiązać każdy obwód prądu stałego, niezależnie od jego złożoności. Wymaga to jednak systematycznego podejścia i cierpliwości w rozwiązywaniu układów równań.

Identyfikacja węzłów i oczek pierwszy krok do sukcesu

Zastosowanie Praw Kirchhoffa zaczyna się od prawidłowego oznaczenia obwodu. To jest absolutnie kluczowe:

• Węzły: Zidentyfikuj wszystkie węzły w obwodzie. Węzeł to punkt, w którym spotykają się co najmniej trzy gałęzie obwodu. Oznacz je literami (np. A, B, C...).
• Gałęzie: Zidentyfikuj wszystkie gałęzie. Gałąź to ścieżka między dwoma węzłami, zawierająca jeden lub więcej elementów.
• Prądy gałęziowe: Przypisz kierunek prądu w każdej gałęzi. Jeśli nie znasz rzeczywistego kierunku, załóż go arbitralnie. Jeśli wynik obliczeń będzie ujemny, oznacza to, że rzeczywisty kierunek jest przeciwny do założonego. Oznacz prądy jako I1, I2, I3...
• Oczka: Zidentyfikuj wszystkie niezależne oczka (pętle) w obwodzie. Niezależne oczko to taka pętla, której nie da się utworzyć z połączenia innych, mniejszych oczek. Zaznacz kierunek obiegu dla każdego oczka (np. zgodnie z ruchem wskazówek zegara).

Budowanie układu równań krok po kroku

Mając prawidłowo oznaczony obwód, możemy przystąpić do tworzenia układu równań liniowych:

1. Równania KCL dla węzłów: Dla każdego niezależnego węzła (z wyjątkiem jednego, który często przyjmujemy jako referencyjny i dla którego równanie jest redundantne) napisz równanie KCL. Suma prądów wpływających do węzła musi być równa sumie prądów wypływających. Pamiętaj o przyjętych kierunkach prądów.

2. Równania KVL dla oczek: Dla każdego niezależnego oczka napisz równanie KVL. Suma spadków napięć na rezystorach i źródeł napięcia w oczku musi być równa zero. Pamiętaj o kierunku obiegu oczka i o tym, że spadek napięcia na rezystorze to I*R (zgodnie z Prawem Ohma).

3. Liczba równań: Upewnij się, że masz tyle samo niezależnych równań, ile jest nieznanych prądów gałęziowych. Zazwyczaj liczba niezależnych równań KCL wynosi (liczba węzłów - 1), a liczba niezależnych równań KVL to (liczba gałęzi - liczba węzłów + 1).

4. Rozwiązanie układu równań: Teraz masz układ równań liniowych, który możesz rozwiązać za pomocą metod algebraicznych (np. podstawiania, eliminacji Gaussa, macierzy). To może być najbardziej pracochłonna część, ale istnieją kalkulatory online i oprogramowanie, które mogą w tym pomóc.

Obliczanie oporu zastępczego z Praw Kirchhoffa

Jeśli Twoim celem jest obliczenie oporu zastępczego całego obwodu, Prawa Kirchhoffa oferują elegancką metodę. Polega ona na założeniu podłączenia "wirtualnego" źródła napięcia U (np. 1V) do zacisków, między którymi chcesz obliczyć opór zastępczy. Następnie, używając Praw Kirchhoffa, obliczasz całkowity prąd I, który wypływa z tego źródła. Gdy masz już U i I, możesz zastosować Prawo Ohma, aby znaleźć opór zastępczy: Rz = U / I. To podejście jest uniwersalne i działa dla każdego obwodu prądu stałego.

Przykład: Rozwiązywanie obwodu Prawami Kirchhoffa

Weźmy obwód, który jest zbyt skomplikowany dla Δ-Y i nie ma oczywistej symetrii. Załóżmy, że chcemy obliczyć opór zastępczy między punktami A i B.

1. Podłącz wirtualne źródło napięcia: Podłącz źródło napięcia U (np. 1V) między punkty A i B. Załóż, że prąd I wypływa z punktu A i wpływa do punktu B.

2. Oznacz węzły i prądy: Zidentyfikuj wszystkie węzły w obwodzie i przypisz kierunki prądów w każdej gałęzi. Oznacz je jako I1, I2, I3 itd. Upewnij się, że masz wystarczającą liczbę prądów do opisania wszystkich gałęzi.

3. Napisz równania KCL: Dla każdego niezależnego węzła napisz równanie sumy prądów. Na przykład, dla węzła X, jeśli prądy I1 i I2 wpływają, a I3 wypływa, równanie to I1 + I2 = I3.

4. Napisz równania KVL: Dla każdego niezależnego oczka napisz równanie sumy napięć. Pamiętaj, że napięcie na rezystorze to I*R. Jeśli w oczku jest źródło napięcia, uwzględnij je. Na przykład, dla oczka z rezystorami R1, R2 i źródłem U, równanie może wyglądać: I1*R1 + I2*R2 = U.

5. Rozwiąż układ równań: Będziesz miał teraz układ równań liniowych z tyloma niewiadomymi (prądami), ile jest niezależnych równań. Rozwiąż ten układ, aby znaleźć wartości wszystkich prądów gałęziowych.

6. Oblicz całkowity prąd I: Sumuj prądy, które wypływają z punktu A (lub wpływają do punktu B), aby uzyskać całkowity prąd I dostarczany przez wirtualne źródło napięcia.

7. Oblicz opór zastępczy: Na koniec, użyj prawa Ohma: Rz = U / I. Jeśli założyłeś U=1V, Rz będzie po prostu 1/I.

To podejście, choć początkowo może wydawać się skomplikowane, jest niezwykle potężne i pozwala na analizę każdego obwodu.

Wykorzystanie symetrii sprytne upraszczanie

Metoda symetrii to zaawansowana technika, która, gdy tylko jest możliwa do zastosowania, potrafi drastycznie uprościć obliczenia. Wymaga jednak pewnej intuicji i umiejętności dostrzegania wzorców w obwodzie. Nie każdy obwód posiada symetrię, ale gdy ją znajdziemy, staje się ona naszym sprzymierzeńcem.

Jak dostrzec symetrię i dlaczego to działa?

Symetrię w obwodzie dostrzegamy, gdy możemy go podzielić na dwie (lub więcej) identyczne części wzdłuż pewnej osi, a te części są połączone w sposób lustrzany. Dlaczego to działa? Ponieważ w obwodzie symetrycznym, punkty leżące symetrycznie względem osi symetrii będą miały identyczne potencjały elektryczne. Jeśli dwa punkty mają ten sam potencjał, oznacza to, że nie płynie między nimi żaden prąd, co pozwala nam na ich połączenie (zwarcie) lub rozłączenie bez wpływu na resztę obwodu.

Techniki "składania" i "zwierania"

Istnieją dwie główne techniki wykorzystujące symetrię:

• Składanie (folding): Jeśli obwód jest symetryczny względem osi przechodzącej przez zaciski, możemy "złożyć" obwód wzdłuż tej osi. Rezystory leżące symetrycznie zostaną połączone równolegle, co upraszcza obwód.
• Zwieranie (shorting): Jeśli obwód jest symetryczny względem osi nieprzechodzącej przez zaciski, punkty na osi symetrii (lub symetryczne punkty poza osią) mogą mieć ten sam potencjał. Możemy wtedy połączyć te punkty ze sobą (zwarcie), co często prowadzi do połączeń szeregowych i równoległych. Alternatywnie, jeśli gałąź leży na osi symetrii i jest połączona z punktami o tym samym potencjale, można ją usunąć (przerwać), ponieważ nie płynie przez nią prąd.

Przykład: Opór zastępczy sześcianu z rezystorów

Obliczanie oporu zastępczego sześcianu, gdzie każda krawędź to rezystor o oporze R, między dwoma przeciwległymi wierzchołkami, jest klasycznym przykładem, gdzie symetria jest nieoceniona:

1. Identyfikacja symetrii: Sześcian ma bardzo wysoką symetrię. Jeśli podłączymy źródło napięcia do dwóch przeciwległych wierzchołków, możemy zauważyć, że wiele punktów w obwodzie będzie miało ten sam potencjał.

2. Punkty o tym samym potencjale: Z wierzchołka wejściowego (A) prąd rozchodzi się na trzy rezystory. Punkty, do których dochodzą te rezystory, są symetryczne i mają ten sam potencjał. Podobnie, punkty, które są połączone z wierzchołkiem wyjściowym (B) trzema rezystorami, również mają ten sam potencjał.

3. Uproszczenie przez zwarcie: Ponieważ punkty o tym samym potencjale można ze sobą połączyć bez zmiany działania obwodu, możemy "zwinąć" obwód. Trzy rezystory wychodzące z A są równoległe do siebie (w sensie, że ich końce są na tym samym potencjale). Podobnie trzy rezystory dochodzące do B są równoległe.

4. Przerysowanie obwodu: Po połączeniu punktów o tym samym potencjale, obwód sześcianu upraszcza się do trzech "warstw" rezystorów połączonych szeregowo. Pierwsza warstwa to trzy rezystory równoległe (wychodzące z A). Druga warstwa to sześć rezystorów równoległych (środkowe krawędzie). Trzecia warstwa to trzy rezystory równoległe (dochodzące do B).

5. Obliczenie oporu zastępczego:

   • Opór pierwszej warstwy: R/3
   • Opór drugiej warstwy: R/6
   • Opór trzeciej warstwy: R/3

   Całkowity opór zastępczy to suma tych oporów, ponieważ warstwy są połączone szeregowo: Rz = R/3 + R/6 + R/3 = 2R/6 + R/6 + 2R/6 = 5R/6.

Jak widać, symetria pozwala na bardzo szybkie i eleganckie rozwiązanie problemu, który bez niej byłby znacznie bardziej skomplikowany.

Narzędzia wspomagające obliczenia Twoi cyfrowi asystenci

W dzisiejszych czasach nie musimy polegać wyłącznie na kartce i długopisie. Dostępne są liczne narzędzia cyfrowe, które mogą wspomóc nas w obliczeniach, a co najważniejsze w weryfikacji naszych wyników. To szczególnie cenne przy skomplikowanych obwodach, gdzie łatwo o pomyłkę.

Popularne symulatory obwodów

Oto kilka popularnych symulatorów, które mogą być bardzo pomocne:

• Falstad Circuit Simulator: Darmowy, przeglądarkowy symulator, który jest niezwykle intuicyjny i pozwala na szybkie budowanie obwodów i obserwowanie przepływu prądu oraz rozkładu napięć w czasie rzeczywistym. Idealny do szybkiej weryfikacji koncepcji.
• LTSpice: Darmowy, profesjonalny symulator SPICE od Analog Devices. Jest bardzo potężny i precyzyjny, choć jego interfejs może być nieco bardziej wymagający dla początkujących. Doskonały do szczegółowej analizy.
• Multisim (National Instruments): Komercyjny symulator, często używany w edukacji. Oferuje bogatą bibliotekę komponentów i intuicyjny interfejs graficzny, co ułatwia budowanie i testowanie obwodów.
• CircuitLab: Przeglądarkowy symulator z darmową wersją podstawową. Łatwy w użyciu, pozwala na szybkie projektowanie i symulację obwodów.

Weryfikacja obliczeń klucz do pewności

Niezależnie od tego, jak pewien jesteś swoich ręcznych obliczeń, zawsze warto je zweryfikować. Symulatory obwodów są do tego idealne. Po prostu zbuduj swój obwód w wybranym programie, podłącz wirtualne źródło napięcia i zmierz prąd całkowity. Następnie, używając prawa Ohma (Rz = U/I), oblicz opór zastępczy i porównaj go ze swoim wynikiem. Ta praktyka nie tylko pomoże Ci wyłapać błędy, ale także pogłębi Twoje zrozumienie działania obwodu i zbuduje Twoją pewność w rozwiązywaniu złożonych problemów.

Wybór metody i unikanie błędów praktyczne wskazówki

Wybór odpowiedniej metody do obliczenia oporu zastępczego w trudnym obwodzie to klucz do efektywnego rozwiązania problemu. Nie ma jednej uniwersalnej metody, która zawsze będzie najlepsza. Musisz nauczyć się elastyczności i oceny, która technika najlepiej pasuje do danej sytuacji. Moje doświadczenie podpowiada, że warto zaczynać od najprostszych rozwiązań, a dopiero potem sięgać po te bardziej zaawansowane.

Kiedy którą metodę wybrać?

• Upraszczanie szeregowo-równoległe: Zawsze zaczynaj od tego. Jeśli widzisz jakiekolwiek proste połączenia, uprość je. To podstawa i często pozwala zredukować złożoność obwodu, zanim przejdziesz do czegoś więcej.
• Transformacja Δ-Y: Idealna, gdy obwód zawiera mostki (np. mostek Wheatstone'a) lub inne konfiguracje, które po prostu nie dają się uprościć szeregowo-równolegle. Szukaj wyraźnych struktur trójkątów lub gwiazd.
• Wykorzystanie symetrii: Jeśli obwód wygląda na bardzo regularny i symetryczny (np. sześcian, siatka), spróbuj tej metody. Może ona drastycznie skrócić czas obliczeń, ale wymaga wprawy w dostrzeganiu symetrii.
• Prawa Kirchhoffa: To Twoja ostatnia deska ratunku i najbardziej uniwersalne narzędzie. Jeśli żadna z powyższych metod nie działa lub obwód jest wyjątkowo złożony i nieregularny, Prawa Kirchhoffa zawsze pozwolą Ci znaleźć rozwiązanie, choć często kosztem dłuższego czasu i większej liczby obliczeń.

Przeczytaj również: Masa czy ciężar? Zrozum różnicę raz na zawsze!

Checklista najczęstszych pomyłek

Aby uniknąć frustracji i błędów, zawsze warto mieć w głowie listę rzeczy do sprawdzenia. Oto najczęstsze pułapki:

• Błędne rozpoznanie połączeń: Czy na pewno rezystory są szeregowo, czy równolegle? Czasem obwód jest tak narysowany, że myli. Zawsze szukaj wspólnych węzłów dla połączeń równoległych i tej samej ścieżki prądu dla szeregowych.
• Niepoprawne zidentyfikowanie układu mostka: Mostek niezrównoważony to sygnał do użycia Δ-Y. Upewnij się, że nie próbujesz go upraszczać w inny sposób.
• Pomyłki algebraiczne: To plaga! Sprawdzaj każdy krok, zwłaszcza przy rozwiązywaniu układów równań i podstawianiu wartości do wzorów Δ-Y. Kalkulator to Twój przyjaciel.
• Niewłaściwe określenie zacisków pomiarowych: Zawsze upewnij się, że obliczasz opór zastępczy między właściwymi punktami obwodu. To jest fundamentalne dla definicji Rz.
• Błędy w kierunkach prądów/napięć (Kirchhoff): Przyjmując kierunki prądów i oczek, bądź konsekwentny. Zły znak w równaniu potrafi zrujnować całe rozwiązanie.
• Brak przerysowywania obwodu: Po każdej transformacji lub uproszczeniu, przerysuj obwód. To pomaga wizualizować zmiany i zapobiega błędom w kolejnych krokach.