W dziedzinie fizyki, a zwłaszcza kinematyki, umiejętność interpretacji wykresów jest kluczowa. Ten artykuł krok po kroku przeprowadzi Cię przez proces obliczania przyspieszenia z wykresu zależności prędkości od czasu (v(t)), wyjaśniając nie tylko sam wzór, ale i stojące za nim zasady. Zrozumiesz, jak nachylenie prostej na takim wykresie bezpośrednio informuje nas o przyspieszeniu i jak unikać najczęstszych błędów.
Obliczanie przyspieszenia z wykresu v(t) zmiana prędkości w czasie
- Przyspieszenie w ruchu prostoliniowym jest równe nachyleniu prostej na wykresie zależności prędkości od czasu v(t).
- Do obliczenia przyspieszenia stosuje się wzór: a = Δv / Δt, gdzie Δv to zmiana prędkości, a Δt to zmiana czasu.
- Linia wznosząca oznacza ruch jednostajnie przyspieszony (a > 0), opadająca jednostajnie opóźniony (a < 0), a pozioma ruch jednostajny (a = 0).
- Aby obliczyć przyspieszenie, należy wybrać dwa punkty na prostej (t1, v1) i (t2, v2) i podstawić ich współrzędne do wzoru.
- Standardową jednostką przyspieszenia w układzie SI jest metr na sekundę kwadrat (m/s²).
- Dla prostych linii na wykresie v(t), przyspieszenie średnie jest równe przyspieszeniu chwilowemu.
Co tak naprawdę pokazuje wykres zależności prędkości od czasu?
Wykres zależności prędkości od czasu, oznaczany jako v(t), to jedno z podstawowych narzędzi w fizyce służących do analizy ruchu. Na osi pionowej (osi Y) przedstawiana jest prędkość obiektu, natomiast na osi poziomej (osi X) czas. Dzięki niemu możemy wizualnie śledzić, jak prędkość ciała zmienia się w czasie, co jest fundamentem do zrozumienia jego ruchu, czy to przyspieszonego, opóźnionego, czy jednostajnego. Dla mnie to zawsze był pierwszy krok do zrozumienia dynamiki danego zjawiska.
Związek między nachyleniem prostej a przyspieszeniem: fundament, który musisz znać
Kluczową informacją, którą musisz zapamiętać, jest to, że przyspieszenie to nic innego jak szybkość zmiany prędkości. Na wykresie v(t) ta szybkość zmiany jest bezpośrednio reprezentowana przez nachylenie prostej. Mówiąc prościej, im bardziej stroma jest linia na wykresie, tym większe jest przyspieszenie (lub opóźnienie). Nachylenie prostej jest równe współczynnikowi kierunkowemu tej prostej, a w kontekście fizyki właśnie przyspieszeniu. To jest absolutna podstawa, bez której trudno ruszyć dalej.
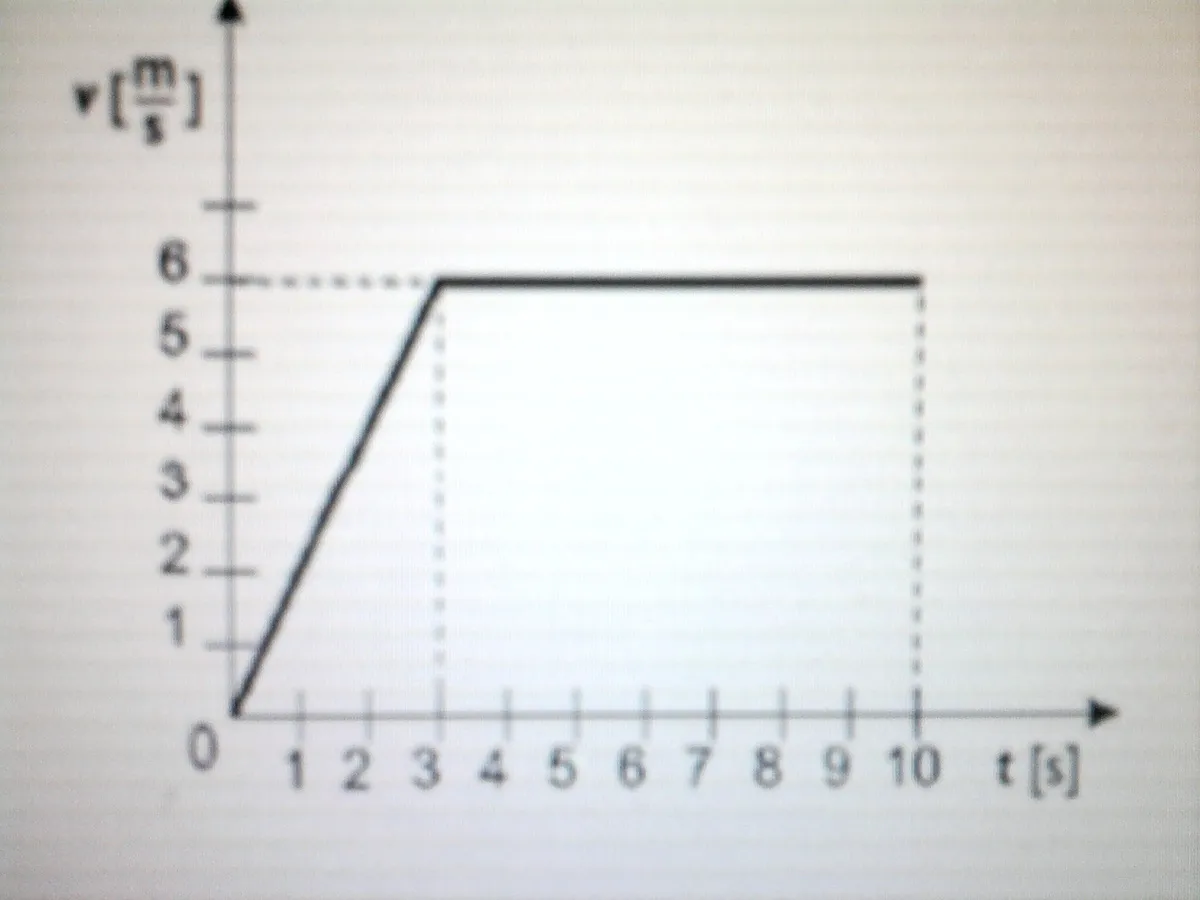
Obliczanie przyspieszenia krok po kroku: uniwersalna metoda
Krok 1: Wybierz dwa kluczowe punkty na wykresie
Aby obliczyć przyspieszenie, potrzebujemy danych z dwóch różnych momentów w czasie. Dlatego pierwszym krokiem jest wybranie dwóch dowolnych punktów na prostej linii wykresu v(t). Ważne, aby były one łatwe do precyzyjnego odczytania z siatki wykresu. Mogą to być początek i koniec analizowanego odcinka ruchu, ale równie dobrze dwa punkty pośrednie. Wybieramy dwa punkty, ponieważ przyspieszenie to zmiana prędkości w pewnym przedziale czasu, a do określenia tego przedziału i zmiany potrzebujemy dwóch "migawki" stanu ruchu.
Krok 2: Poprawnie odczytaj współrzędne (czas i prędkość)
Po wybraniu punktów (nazwijmy je Punkt 1 i Punkt 2), musisz dokładnie odczytać ich współrzędne. Dla Punktu 1 będą to czas początkowy `t1` i prędkość początkowa `v1`. Dla Punktu 2 będą to czas końcowy `t2` i prędkość końcowa `v2`. Zawsze zwracaj uwagę na skalę osi to częste źródło pomyłek. Precyzja w tym kroku jest absolutnie kluczowa dla uzyskania prawidłowego wyniku. Ja zawsze dwukrotnie sprawdzam odczyty, zanim przejdę do obliczeń.
Krok 3: Zastosuj fundamentalny wzór a = Δv / Δt
Gdy masz już wszystkie współrzędne, czas na zastosowanie najważniejszego wzoru. Przyspieszenie (a) obliczamy jako zmianę prędkości (Δv) podzieloną przez zmianę czasu (Δt). Zmiana prędkości Δv to nic innego jak różnica między prędkością końcową a początkową (`v2 - v1`). Analogicznie, zmiana czasu Δt to różnica między czasem końcowym a początkowym (`t2 - t1`).
Oto pełny wzór:
a = (v2 - v1) / (t2 - t1)
Krok 4: Nie zapomnij o jednostkach! Jak poprawnie je zapisać?
W fizyce jednostki są tak samo ważne jak liczby! Standardową jednostką przyspieszenia w układzie SI jest metr na sekundę kwadrat (m/s²). Jeśli na wykresie prędkość jest podana w kilometrach na godzinę (km/h), a czas w godzinach, wynik przyspieszenia otrzymasz w km/h². W wielu zadaniach fizycznych konieczne będzie przeliczenie tych jednostek na metry i sekundy, aby wynik był zgodny z układem SI. Pamiętaj, aby zawsze podawać wynik z odpowiednią jednostką to pokazuje pełne zrozumienie zagadnienia.
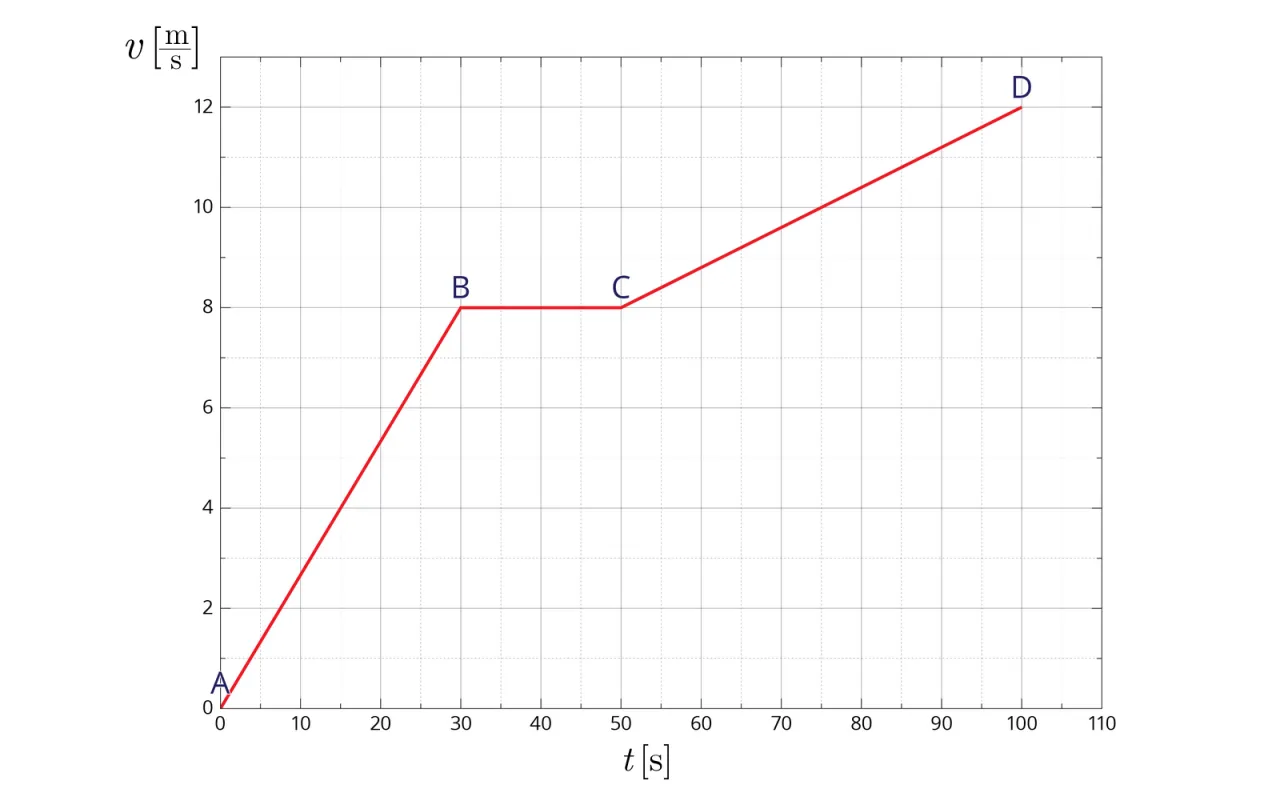
Różne rodzaje ruchu na wykresie v(t): praktyczne przykłady
Ruch jednostajnie przyspieszony: gdy linia pnie się w górę
Jeśli na wykresie v(t) widzisz prostą linię, która wznosi się do góry (ma dodatnie nachylenie), oznacza to, że mamy do czynienia z ruchem jednostajnie przyspieszonym. W takim przypadku prędkość obiektu rośnie w stałym tempie, a przyspieszenie jest stałe i ma wartość dodatnią (a > 0). Samochód ruszający ze świateł to doskonały przykład takiego ruchu.
Przykład obliczeniowy dla przyspieszenia dodatniego
Załóżmy, że na wykresie v(t) mamy następujące punkty:
- Wybieramy punkty:
- Punkt 1: `t1 = 0 s`, `v1 = 0 m/s`
- Punkt 2: `t2 = 5 s`, `v2 = 10 m/s`
a = (10 m/s - 0 m/s) / (5 s - 0 s)
a = 10 m/s / 5 s
a = 2 m/s²
W tym przypadku przyspieszenie wynosi 2 m/s², co oznacza, że prędkość obiektu wzrasta o 2 metry na sekundę co sekundę.
Ruch jednostajnie opóźniony: co oznacza linia opadająca?
Gdy na wykresie v(t) prosta linia opada w dół (ma ujemne nachylenie), świadczy to o ruchu jednostajnie opóźnionym. Oznacza to, że prędkość obiektu maleje w stałym tempie, a przyspieszenie jest stałe i ma wartość ujemną (a < 0). To typowa sytuacja, gdy samochód hamuje przed przeszkodą.
Przykład obliczeniowy dla przyspieszenia ujemnego (opóźnienia)
Rozważmy odcinek wykresu, gdzie obiekt zwalnia:
- Wybieramy punkty:
- Punkt 1: `t1 = 10 s`, `v1 = 15 m/s`
- Punkt 2: `t2 = 15 s`, `v2 = 5 m/s`
a = (5 m/s - 15 m/s) / (15 s - 10 s)
a = -10 m/s / 5 s
a = -2 m/s²
Ujemny znak przyspieszenia (-2 m/s²) wskazuje, że obiekt zwalnia, czyli jego prędkość maleje o 2 metry na sekundę co sekundę.
Ruch jednostajny: dlaczego pozioma linia oznacza zerowe przyspieszenie?
Jeśli na wykresie v(t) widzimy poziomą linię (równoległą do osi czasu), oznacza to, że prędkość obiektu jest stała. W takim przypadku mamy do czynienia z ruchem jednostajnym. Skoro prędkość się nie zmienia, to zmiana prędkości (Δv) wynosi zero. A jeśli Δv = 0, to i przyspieszenie musi być równe zeru. To logiczne brak zmiany prędkości oznacza brak przyspieszenia. To najprostszy przypadek, ale często bywa mylący dla początkujących.
Najczęstsze pułapki i błędy: jak ich unikać?
Mylenie wykresu v(t) z wykresem drogi s(t)
Jednym z najczęstszych błędów jest mylenie wykresu prędkości od czasu (v(t)) z wykresem drogi od czasu (s(t)). Pamiętaj, że na wykresie s(t) nachylenie prostej reprezentuje prędkość, natomiast na wykresie v(t) nachylenie prostej reprezentuje przyspieszenie. To fundamentalna różnica, która często prowadzi do błędnych interpretacji wyników. Zawsze najpierw sprawdź, jaka wielkość jest na osi pionowej!
Błędy przy odczytywaniu wartości z osi wykresu
Nawet najmniejszy błąd w odczycie wartości z osi wykresu może całkowicie zafałszować wynik końcowy. Zawsze uważnie sprawdzaj skalę obu osi. Czy jedna kratka to 1 jednostka, czy może 2, 5, a nawet 0.5? Upewnij się, że odczytujesz wartości z odpowiednią precyzją, zwłaszcza gdy punkty nie leżą idealnie na przecięciach linii siatki. Ja sam nieraz musiałem wracać do tego kroku, bo pośpiech zgubił mnie w obliczeniach.
Prawidłowa interpretacja znaku wyniku: kiedy przyspieszenie jest dodatnie, a kiedy ujemne?
Znak przyspieszenia ma ogromne znaczenie i nie jest przypadkowy. Dodatnie przyspieszenie (a > 0) oznacza, że obiekt przyspiesza (jego prędkość rośnie) w kierunku zgodnym z przyjętym dodatnim kierunkiem osi. Ujemne przyspieszenie (a < 0) oznacza, że obiekt zwalnia (jego prędkość maleje) lub przyspiesza w kierunku przeciwnym do przyjętego dodatniego kierunku. Często ujemne przyspieszenie nazywamy opóźnieniem. Zrozumienie tego znaku jest kluczowe dla pełnej interpretacji ruchu.
Co zrobić, gdy wykres nie jest linią prostą?
Czym jest przyspieszenie średnie i jak je obliczyć?
Wszystkie dotychczasowe przykłady dotyczyły wykresów v(t), które były liniami prostymi. Co jednak, gdy wykres jest krzywą? W takim przypadku ruch nie jest jednostajnie zmienny, a przyspieszenie nie jest stałe. Wciąż możemy jednak obliczyć przyspieszenie średnie w danym przedziale czasu. Wzór `a = Δv / Δt` nadal ma zastosowanie po prostu wybieramy dwa punkty na krzywej odpowiadające początkowi i końcowi interesującego nas przedziału czasu. Pamiętaj jednak, że wynik będzie średnią wartością przyspieszenia, a nie wartością chwilową.
Przeczytaj również: Dlaczego dźwięk nie rozchodzi się w próżni? Prawda o kosmosie.
Wprowadzenie do przyspieszenia chwilowego: co mówi nam styczna do krzywej?
Jeśli chcemy poznać przyspieszenie chwilowe, czyli przyspieszenie w konkretnym momencie czasu, sprawa staje się nieco bardziej skomplikowana. Dla wykresu, który nie jest linią prostą, przyspieszenie chwilowe jest równe nachyleniu stycznej do krzywej wykresu v(t) w danym punkcie czasowym. To już bardziej zaawansowane zagadnienie, często wymagające narzędzi rachunku różniczkowego. Jest to jednak istotne dla pełnego zrozumienia ruchu niejednostajnie zmiennego i pokazuje, jak dynamicznie zmienia się przyspieszenie w każdym punkcie toru.

