Obliczanie pola trapezu prostokątnego może wydawać się skomplikowane, ale w rzeczywistości jest to zadanie, z którym każdy może sobie poradzić, mając odpowiedni wzór i jasne instrukcje. W tym artykule pokażę Ci krok po kroku, jak to zrobić, a także podpowiem, co zrobić, gdy brakuje niektórych danych. Moim celem jest, abyś po przeczytaniu tego tekstu czuł się pewnie w obliczeniach i potrafił zastosować tę wiedzę w praktyce.
Obliczanie pola trapezu prostokątnego: prosty wzór i praktyczne wskazówki
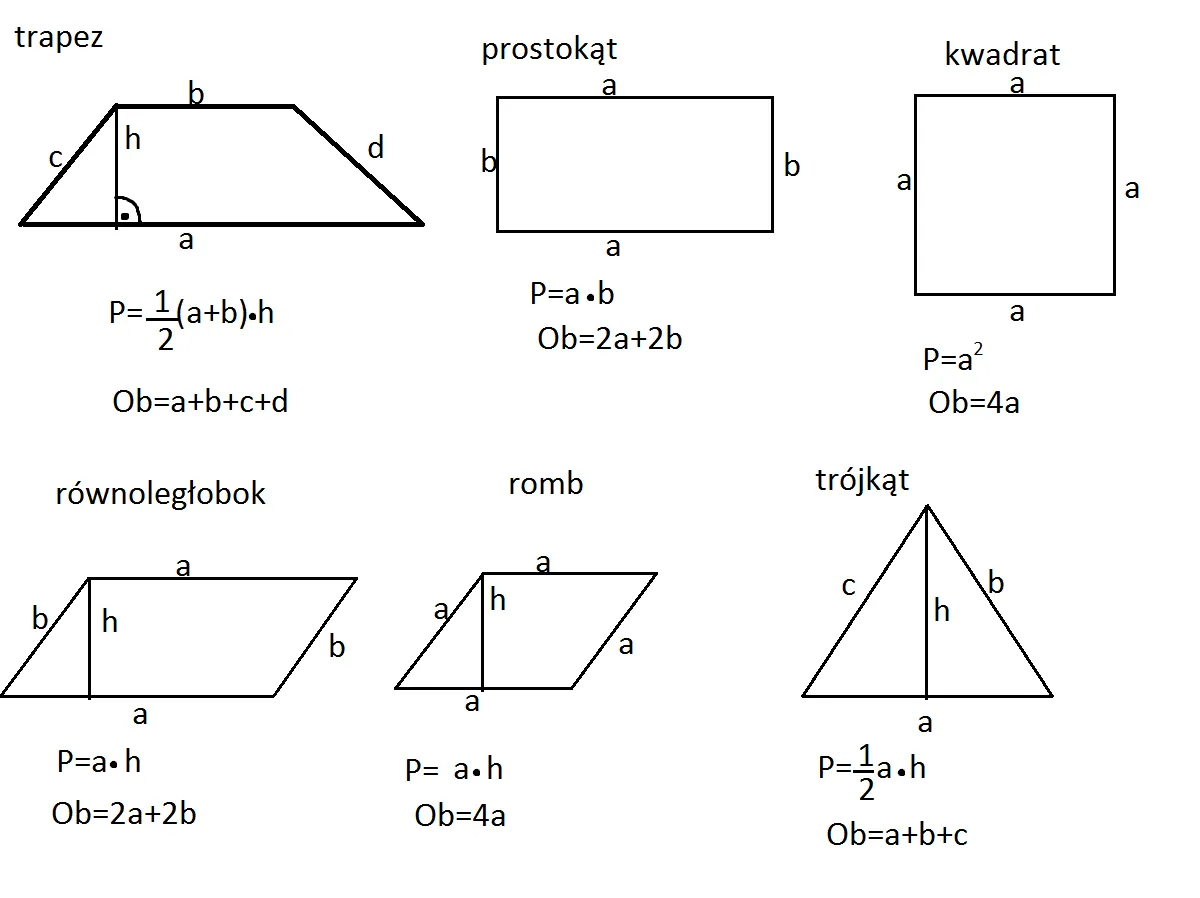
- Wzór na pole trapezu prostokątnego to P = ½ * (a + b) * h, gdzie 'a' i 'b' to podstawy, a 'h' to wysokość.
- W trapezie prostokątnym jedno z ramion jest prostopadłe do podstaw i pełni rolę wysokości.
- Gdy brakuje danych (np. wysokości lub jednej z podstaw), często wykorzystuje się twierdzenie Pitagorasa, dzieląc trapez na prostokąt i trójkąt prostokątny.
- Praktyczne zastosowania obejmują obliczanie powierzchni w budownictwie (np. ściany na poddaszu) czy projektowaniu ogrodów.
- Najczęstsze błędy to mylenie podstaw z ramionami oraz zapominanie o podzieleniu wyniku przez 2.
Trapez prostokątny dlaczego jest wyjątkowy?
Trapez prostokątny wyróżnia się na tle innych trapezów swoją specyficzną budową. Posiada on dwa kąty proste zawsze są to kąty przy jednym z ramion. To właśnie to ramię jest prostopadłe do obu podstaw, co jest jego kluczową cechą. W przeciwieństwie do ogólnego trapezu, gdzie wysokość trzeba często wyznaczać dodatkowo, w trapezie prostokątnym jedno z ramion "samo" jest wysokością, co znacznie upraszcza wiele obliczeń.
Jedno ramię, dwie role jak wysokość jest "wbudowana" w figurę?
To, co czyni trapez prostokątny tak wygodnym w obliczeniach, to fakt, że jedno z jego ramion pełni podwójną rolę. Jest nie tylko bokiem figury, ale także jej wysokością. Dzieje się tak, ponieważ to ramię jest prostopadłe do obu podstaw trapezu. Dzięki temu, jeśli znasz długość tego ramienia, automatycznie znasz wysokość trapezu. Nie musisz wykonywać żadnych dodatkowych konstrukcji czy obliczeń, aby ją znaleźć, co jest sporym ułatwieniem.
Wzór na pole trapezu prostokątnego twoja podstawowa ściągawka
Przejdźmy teraz do sedna, czyli do wzoru, który pozwoli Ci obliczyć pole trapezu prostokątnego. Pamiętaj, że ten sam wzór jest uniwersalny dla wszystkich trapezów, ale w przypadku prostokątnego jego zastosowanie jest często jeszcze prostsze.
Poznaj wzór: P = ½ * (a + b) * h
Oto fundamentalny wzór, który musisz znać:
P = ½ * (a + b) * h
Co oznaczają symbole a, b i h? Dokładne objaśnienie
Aby poprawnie zastosować wzór, musisz wiedzieć, co oznaczają poszczególne symbole:
- a: To długość jednej z podstaw trapezu. Podstawy to zawsze te dwa boki, które są do siebie równoległe. Nie ma znaczenia, czy nazwiesz dłuższą podstawę 'a', a krótszą 'b', czy odwrotnie wynik będzie ten sam, ponieważ dodawanie jest przemienne.
- b: To długość drugiej podstawy trapezu. Podobnie jak 'a', jest to jeden z równoległych boków.
- h: To wysokość trapezu. Jest to odcinek prostopadły do obu podstaw. W przypadku trapezu prostokątnego, jak już wspomniałem, 'h' to po prostu długość tego ramienia, które jest prostopadłe do podstaw.
Jak obliczyć pole trapezu prostokątnego krok po kroku?
Aby ułatwić zrozumienie, przeprowadzę Cię przez proces obliczeń na konkretnym przykładzie. Zobaczysz, że to naprawdę proste!
-
Krok 1: Zidentyfikuj podstawy (a i b) oraz wysokość (h)
Na początek musisz dokładnie przyjrzeć się swojemu trapezowi i zidentyfikować potrzebne wymiary. Załóżmy, że mamy trapez prostokątny, w którym:
- Dłuższa podstawa (a) = 10 cm
- Krótsza podstawa (b) = 6 cm
- Ramię prostopadłe do podstaw, czyli wysokość (h) = 4 cm
-
Krok 2: Podstaw dane do wzoru zobacz to na konkretnych liczbach
Teraz, gdy masz już wszystkie dane, podstaw je do wzoru P = ½ * (a + b) * h:
P = ½ * (10 cm + 6 cm) * 4 cm
-
Krok 3: Wykonaj obliczenia i uzyskaj wynik proste i bez błędów
Przeprowadźmy obliczenia krok po kroku:
- Najpierw dodaj podstawy: 10 cm + 6 cm = 16 cm
- Następnie pomnóż sumę przez wysokość: 16 cm * 4 cm = 64 cm²
- Na koniec podziel wynik przez 2: 64 cm² / 2 = 32 cm²
Zatem pole naszego trapezu prostokątnego wynosi 32 cm². Pamiętaj o prawidłowych jednostkach pole zawsze wyrażamy w jednostkach kwadratowych!
Co zrobić, gdy brakuje danych? Znajdź wysokość lub podstawę
Nie zawsze wszystkie potrzebne dane są podane wprost. Czasem trzeba je "wykombinować", ale nie martw się to również jest do zrobienia, często z pomocą jednego z najważniejszych twierdzeń w geometrii.
Scenariusz 1: Masz podane podstawy i ukośne ramię jak znaleźć wysokość?
Wyobraź sobie, że znasz długości obu podstaw (a i b) oraz długość ukośnego ramienia (c), ale nie znasz wysokości (h). W takiej sytuacji Twoim najlepszym sprzymierzeńcem będzie twierdzenie Pitagorasa. Aby je zastosować, musisz narysować wysokość z wierzchołka kąta rozwartego na dłuższą podstawę. W ten sposób utworzysz prostokąt i trójkąt prostokątny. Boki tego trójkąta to: szukana wysokość (h), różnica długości podstaw (a - b) oraz ukośne ramię (c), które w tym trójkącie będzie przeciwprostokątną.Twierdzenie Pitagorasa w akcji: Twój najlepszy przyjaciel w trapezie
Twierdzenie Pitagorasa mówi, że w trójkącie prostokątnym suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej: a² + b² = c². W naszym przypadku, dla utworzonego trójkąta prostokątnego, będzie to wyglądać tak:
h² + (a - b)² = c²
Przykład: Jeśli a = 10 cm, b = 6 cm, a ukośne ramię c = 5 cm, to różnica podstaw wynosi (10 - 6) = 4 cm. Wtedy:
h² + 4² = 5²
h² + 16 = 25
h² = 25 - 16
h² = 9
h = √9 = 3 cm
Znalazłeś wysokość! Teraz możesz obliczyć pole trapezu.
Scenariusz 2: Znasz wysokość, jedną podstawę i ramię jak obliczyć drugą podstawę?
A co, jeśli znasz wysokość (h), jedną podstawę (np. 'a') i ukośne ramię (c), a musisz znaleźć drugą podstawę ('b')? Postępujesz podobnie. Rysujesz wysokość, tworząc trójkąt prostokątny. Z twierdzenia Pitagorasa (h² + x² = c², gdzie 'x' to brakujący fragment podstawy) obliczasz długość 'x'. Następnie, jeśli 'a' to dłuższa podstawa, 'b' będzie równe a - x. Jeśli 'a' to krótsza podstawa, to dłuższa podstawa będzie równa a + x. To pozwala na znalezienie brakującej podstawy i kontynuowanie obliczeń pola.
Najczęstsze pułapki i błędy sprawdź, czego unikać
Podczas obliczania pola trapezu prostokątnego łatwo o drobne pomyłki. Chcę Cię przed nimi ostrzec, abyś mógł ich unikać.
-
Błąd #1: Mylenie podstaw z ramionami we wzorze
To bardzo częsty błąd. Pamiętaj, że we wzorze P = ½ * (a + b) * h, 'a' i 'b' to zawsze długości boków równoległych, czyli podstaw. Ramiona to te boki, które nie są równoległe (w trapezie prostokątnym jedno z nich jest wysokością, a drugie jest ukośne). Podstawienie długości ramion zamiast podstaw da całkowicie błędny wynik.
-
Błąd #2: Zapominanie o podzieleniu przez 2 dlaczego to kluczowe?
Wzór na pole trapezu zawiera czynnik ½, co oznacza, że sumę podstaw pomnożoną przez wysokość zawsze musisz podzielić przez 2. Zapomnienie o tym kroku sprawi, że Twój wynik będzie dwukrotnie zawyżony. To jakbyś obliczył pole prostokąta, który ma jedną podstawę jako sumę podstaw trapezu, a drugą jako wysokość trapez to "połówka" takiego prostokąta (w pewnym uproszczeniu).
-
Błąd #3: Niepoprawne obliczenia z twierdzenia Pitagorasa
Jeśli musisz użyć twierdzenia Pitagorasa do znalezienia brakujących danych, upewnij się, że poprawnie identyfikujesz przyprostokątne i przeciwprostokątną. Przeciwprostokątna to zawsze najdłuższy bok, leżący naprzeciwko kąta prostego. Błędne podstawienie wartości do wzoru a² + b² = c² może prowadzić do poważnych błędów w dalszych obliczeniach.
Gdzie w praktyce wykorzystasz obliczanie pola trapezu?
Może się wydawać, że obliczanie pola trapezu to tylko szkolna teoria, ale w rzeczywistości ma ono wiele praktycznych zastosowań w życiu codziennym. Jako Igor Lis, często widzę, jak przydaje się to w różnych projektach.
-
Remont mieszkania: Obliczanie powierzchni ścian na poddaszu
Jeśli masz mieszkanie na poddaszu, z pewnością spotkałeś się ze ścianami o nietypowych kształtach. Często są to właśnie trapezy prostokątne! Aby kupić odpowiednią ilość farby, tapety czy paneli ściennych, musisz precyzyjnie obliczyć ich powierzchnię. Znajomość wzoru na pole trapezu prostokątnego jest tu absolutnie kluczowa, aby uniknąć marnowania materiałów lub ich niedoboru.
-
Przeczytaj również: Jak obliczyć błąd bezwzględny i względny? Przewodnik krok po kroku
Prace w ogrodzie: Planowanie nietypowych rabat i trawników
Projektowanie ogrodu to sztuka, a czasem wymaga też matematyki. Jeśli chcesz stworzyć nietypową rabatę kwiatową, trawnik czy ścieżkę o kształcie trapezu prostokątnego, musisz wiedzieć, ile materiału (ziemi, nasion trawy, kostki brukowej) będziesz potrzebować. Obliczenie pola pozwoli Ci dokładnie zaplanować zakupy i uniknąć niepotrzebnych kosztów.

