Ten artykuł to Twój praktyczny przewodnik po świecie kątów naprzemianległych i odpowiadających. Dowiesz się, jak je skutecznie rozpoznawać na rysunkach geometrycznych, wykorzystując proste metody wizualne, co pozwoli Ci bezbłędnie rozwiązywać zadania i zrozumieć kluczowe zasady geometrii.
Odnajdywanie kątów naprzemianległych i odpowiadających proste metody i kluczowe zasady
- Kąty naprzemianległe i odpowiadające powstają, gdy dwie proste są przecięte sieczną.
- Ich miary są równe tylko wtedy, gdy proste są równoległe (k || l).
- Do identyfikacji kątów odpowiadających użyj "metody litery F".
- Do identyfikacji kątów naprzemianległych wewnętrznych użyj "metody litery Z".
- Kluczowe jest rozróżnienie kątów naprzemianległych wewnętrznych i zewnętrznych.
- Uważaj na częste błędy, takie jak mylenie ich z kątami przyległymi lub zakładanie równości miar, gdy proste nie są równoległe.
Czym są proste równoległe i sieczna? Fundament całej układanki
Zanim zagłębimy się w świat kątów, musimy upewnić się, że rozumiemy podstawowe elementy, które je tworzą. Wyobraź sobie dwie proste, które nigdy się nie spotykają, niezależnie od tego, jak daleko je poprowadzisz to są właśnie proste równoległe, które oznaczamy jako k || l. Teraz wyobraź sobie trzecią prostą, która przecina te dwie pierwsze. Nazywamy ją sieczną (t). To właśnie ten układ, te trzy proste, tworzą scenę, na której pojawiają się nasze kąty naprzemianległe i odpowiadające. Bez nich nie byłoby o czym mówić w kontekście tych konkretnych zależności.
Kąty wierzchołkowe i przyległe: szybkie przypomnienie, by unikać błędów
Wiem z doświadczenia, że często zdarza się mylić kąty naprzemianległe czy odpowiadające z innymi rodzajami kątów. Dlatego szybkie przypomnienie o kątach wierzchołkowych i przyległych jest kluczowe. Kąty wierzchołkowe to takie, które mają wspólny wierzchołek, a ich ramiona są wzajemnie swoimi przedłużeniami. Ich najważniejszą cechą jest to, że zawsze mają równe miary. Pamiętaj o tym, bo to bardzo przydatne narzędzie w zadaniach.
Z kolei kąty przyległe mają wspólne ramię i wspólny wierzchołek, a ich pozostałe ramiona tworzą linię prostą. Co to oznacza w praktyce? To, że ich suma miar zawsze wynosi 180°. Te dwa typy kątów często pojawiają się obok naprzemianległych i odpowiadających, a ich znajomość pozwala na "przenoszenie" informacji o miarach kątów w obrębie rysunku.
Kąty odpowiadające: Jak rozpoznać je bezbłędnie za każdym razem?
Definicja dla bystrzaków: Gdzie dokładnie leżą kąty odpowiadające?
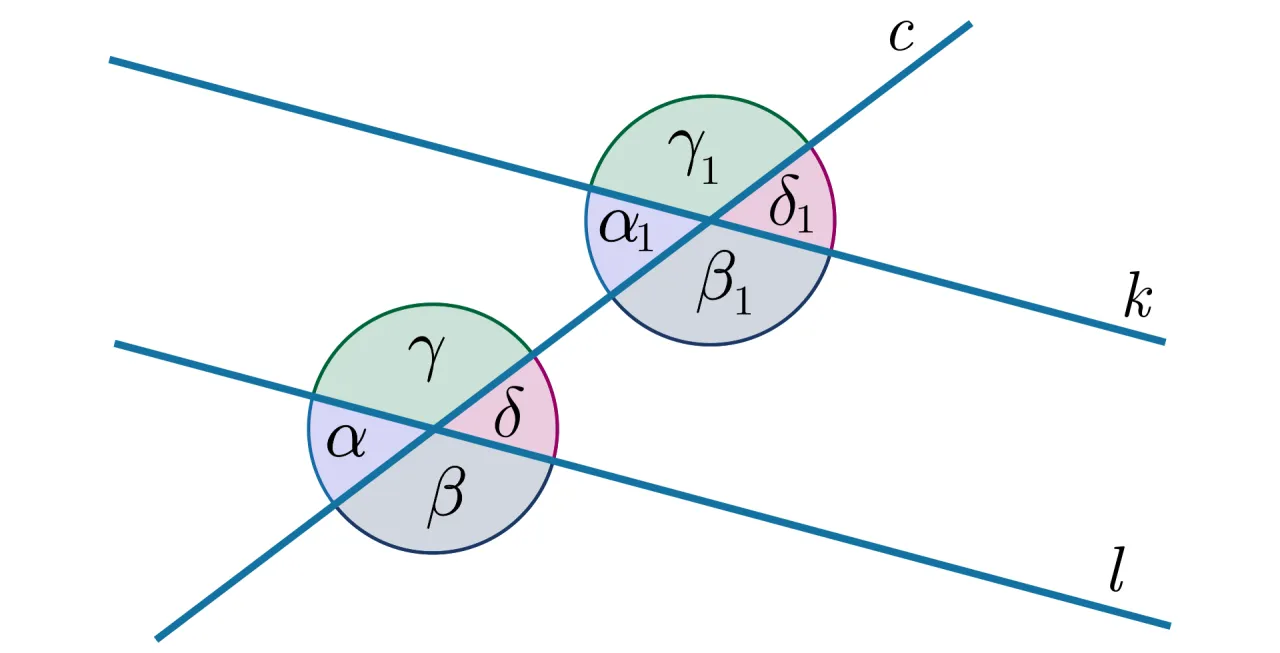
Przejdźmy do sedna. Kąty odpowiadające to kąty, które leżą po tej samej stronie siecznej. Co więcej, jeden z nich jest kątem wewnętrznym (czyli znajduje się między dwoma prostymi k i l), a drugi jest kątem zewnętrznym (czyli leży poza tymi prostymi). Wyobraź sobie, że sieczna to granica, a te kąty są po tej samej stronie granicy, ale jeden w środku "terytorium" prostych, a drugi na zewnątrz.
Metoda na literę "F": niezawodny trik wizualny, który zawsze działa
Dla mnie i dla wielu moich uczniów, "metoda litery F" to absolutny strzał w dziesiątkę, jeśli chodzi o rozpoznawanie kątów odpowiadających. Spróbuj "zobaczyć" na rysunku kształt litery F. Może być ona odwrócona, obrócona, a nawet lustrzana. Ważne, abyś dostrzegł ten charakterystyczny układ: dwie równoległe linie tworzące "poziome" kreski litery F, a sieczna jako "pionowa" kreska. Kąty, które znajdują się w tych samych "rogach" litery F, to właśnie kąty odpowiadające. Gdy już raz to zobaczysz, trudno będzie Ci je pomylić.
Jaka jest ich najważniejsza właściwość, gdy proste są równoległe?
Kluczowa informacja, którą musisz zapamiętać, to: jeśli proste k i l są równoległe (k || l), to miary kątów odpowiadających są równe. To jest fundament, na którym opiera się większość zadań z tego zakresu. Ale co ważne, ta zasada działa też w drugą stronę! Jeśli uda Ci się udowodnić, że para kątów odpowiadających ma równe miary, to automatycznie wiesz, że proste, które je tworzą, muszą być równoległe. To potężne narzędzie do dowodzenia równoległości w geometrii.
Kąty naprzemianległe: Twój drugi as w rękawie geometrii
Kąty naprzemianległe wewnętrzne vs. zewnętrzne: czym się różnią?
- Kąty naprzemianległe wewnętrzne: Leżą między dwiema prostymi (k i l) i po przeciwnych stronach siecznej (t). To właśnie one są najczęściej spotykane w zadaniach szkolnych i na nich skupia się większość uwagi.
- Kąty naprzemianległe zewnętrzne: Leżą na zewnątrz dwóch prostych (k i l) i również po przeciwnych stronach siecznej (t). Choć rzadziej pojawiają się w podstawowych zadaniach, warto wiedzieć o ich istnieniu i właściwościach.
W praktyce, gdy mówimy o kątach naprzemianległych, zazwyczaj mamy na myśli te wewnętrzne. Ich zrozumienie jest absolutnie fundamentalne.
Metoda na literę "Z": zobacz, jak łatwo znaleźć kąty naprzemianległe wewnętrzne
Podobnie jak w przypadku kątów odpowiadających, mamy tu fantastyczną mnemotechnikę wizualną "metodę litery Z". Aby znaleźć kąty naprzemianległe wewnętrzne, poszukaj na rysunku kształtu litery Z. Może być ona oczywiście odwrócona lub lustrzana. Kąty, które znajdują się w "rogach" tej litery Z, to właśnie kąty naprzemianległe wewnętrzne. Ta metoda jest niezwykle intuicyjna i pozwala szybko zidentyfikować te kąty, nawet na skomplikowanych rysunkach. Spróbuj narysować kilka prostych i sieczną, a następnie "wyszukaj" literę Z zobaczysz, jak to działa!
Dlaczego ich miary są równe? Zrozum zasadę, a nie tylko zapamiętaj
Zastanawiałeś się kiedyś, dlaczego miary kątów naprzemianległych są równe, gdy proste są równoległe? To nie jest magia, to czysta geometria! Możesz to sobie wyobrazić w ten sposób: jeśli proste k i l są równoległe, to sieczna przecina je "pod tym samym kątem". Gdybyś "przesunął" jeden z wierzchołków kąta naprzemianległego wewnętrznego wzdłuż siecznej do drugiego wierzchołka, to ramiona kątów idealnie by się nałożyły. To pokazuje, że te kąty są w istocie "takie same", tylko w różnych miejscach. Ta intuicja pomaga zrozumieć, że równość miar nie jest przypadkowa, ale wynika bezpośrednio z definicji prostych równoległych i ich wzajemnego położenia względem siecznej.
Praktyczny przewodnik: Jak znaleźć kąty naprzemianległe i odpowiadające krok po kroku
Teraz, gdy znasz już definicje i metody wizualne, przejdźmy do praktyki. Oto sprawdzona ścieżka, którą polecam moim uczniom:
-
Zidentyfikuj podstawowe elementy: Na każdym rysunku geometrycznym, niezależnie od jego złożoności, zacznij od odnalezienia dwóch prostych (oznaczmy je jako k i l) oraz przecinającej je siecznej (t). To jest absolutna podstawa, bez której nie ruszysz dalej.
-
Sprawdź warunek równoległości: Zawsze, ale to zawsze, sprawdź, czy w zadaniu jest informacja o równoległości prostych (k || l) lub czy możesz ją w jakiś sposób wywnioskować. Pamiętaj, że równość miar kątów naprzemianległych i odpowiadających zachodzi tylko i wyłącznie wtedy, gdy proste są równoległe. To jest krytyczny warunek, którego nie możesz pominąć!
-
Zastosuj metody wizualne: Gdy już masz zidentyfikowane proste i sieczną, a także wiesz, czy proste są równoległe, użyj "metody F" dla kątów odpowiadających i "metody Z" dla kątów naprzemianległych wewnętrznych. Spróbuj "narysować" te litery palcem na rysunku, aby wizualnie odnaleźć szukane pary kątów. To naprawdę działa!
-
Wykorzystaj właściwości kątów: Po zidentyfikowaniu kątów i potwierdzeniu równoległości prostych, możesz śmiało wykorzystać równość ich miar. To pozwoli Ci obliczyć nieznane kąty, udowodnić równoległość innych odcinków lub rozwiązać całe zadanie geometryczne. Pamiętaj, że geometria to często gra w "przenoszenie" informacji o kątach.
Najczęstsze pułapki i błędy: Na co uważać, rozwiązując zadania?
Jako doświadczony nauczyciel wiem, gdzie najczęściej pojawiają się problemy. Poniżej przedstawiam najczęstsze błędy, na które musisz uważać.
Mylenie kątów naprzemianległych z jednostronnymi: subtelna, ale kluczowa różnica
To bardzo częsta pułapka! Obok kątów naprzemianległych i odpowiadających, istnieją również kąty jednostronne (wewnętrzne i zewnętrzne). Kąty jednostronne wewnętrzne leżą po tej samej stronie siecznej i między prostymi. Kluczowa różnica polega na tym, że w przypadku prostych równoległych, suma miar kątów jednostronnych wewnętrznych (i zewnętrznych) wynosi 180°, a nie są one sobie równe! Mylenie tej zasady z równością kątów naprzemianległych to błąd, który może kosztować Cię punkty w zadaniu. Zawsze dokładnie sprawdzaj, czy kąty leżą po tej samej, czy po przeciwnych stronach siecznej.
Zakładanie równości kątów, gdy proste NIE SĄ równoległe
To chyba największy i najczęściej popełniany błąd! Wielu uczniów automatycznie zakłada, że miary kątów naprzemianległych lub odpowiadających są równe, nawet jeśli w zadaniu nie ma żadnej informacji o równoległości prostych. Musisz pamiętać, że równość miar tych kątów jest konsekwencją równoległości prostych, a nie ich domyślnym stanem. Jeśli proste nie są równoległe, to te kąty po prostu nie są sobie równe! Zawsze szukaj symbolu równoległości (||) lub wyraźnego stwierdzenia w treści zadania, zanim zastosujesz zasadę równości miar.
Przeczytaj również: Jak obliczyć błąd bezwzględny i względny? Przewodnik krok po kroku
Ignorowanie kątów wierzchołkowych i przyległych jako pomocniczych narzędzi
Wspominałem o nich na początku i wracam do tego, bo to niezwykle ważne. Kąty wierzchołkowe i przyległe, choć nie są głównym tematem, są Twoimi sprzymierzeńcami w rozwiązywaniu zadań. Bardzo często zdarza się, że dany kąt nie jest bezpośrednio kątem naprzemianległym ani odpowiadającym do tego, którego szukasz. Jednak dzięki kątom wierzchołkowym możesz "przenieść" jego miarę do pozycji, w której stanie się on kątem odpowiadającym lub naprzemianległym. Podobnie z kątami przyległymi jeśli znasz jeden, możesz łatwo obliczyć drugi. Nie ignoruj tych prostych, ale potężnych narzędzi!

