Logarytmy dla opornych: Zrozum potęgi na nowo!

Logarytmy. Już sama nazwa potrafi wywołać dreszcze, prawda? Wiem to doskonale, bo przez lata widziałem, jak wielu uczniów i studentów zmaga się z tym zagadnieniem. Często wydają się one skomplikowane i abstrakcyjne, ale obiecuję Ci, że to tylko pozory. W rzeczywistości logarytmy są bardzo proste, jeśli tylko podejdzie się do nich w odpowiedni sposób i zrozumie ich prawdziwą naturę. W tym artykule pokażę Ci, jak oswoić logarytmy od absolutnych podstaw, bez zbędnego żargonu i skomplikowanych definicji. Gotowy na to, by raz na zawsze zrozumieć, o co w nich chodzi?

Logarytmy: dlaczego bywają wyzwaniem i jak je oswoić?

Z mojego doświadczenia wynika, że logarytmy często budzą strach, bo są przedstawiane w sposób zbyt abstrakcyjny, od razu z mnóstwem wzorów i regułek. Tymczasem to nic innego jak inna perspektywa na znane już potęgowanie. Wyobraź sobie, że umiesz już doskonale chodzić do przodu, a teraz ktoś każe Ci nauczyć się chodzić do tyłu. To trochę dziwne na początku, prawda? Ale przecież nadal umiesz chodzić! Tak samo jest z logarytmami jeśli rozumiesz potęgi, masz już 90% sukcesu. Logarytmy po prostu "odwracają" to myślenie.

Czym tak naprawdę jest logarytm? Wyjaśnienie na prostych przykładach

Zacznijmy od formalnej definicji, ale od razu ją uprościmy, obiecuję! Logarytm o podstawie a z liczby b to taka liczba c, że a podniesione do potęgi c daje b. Zapisujemy to tak: logₐb = c ⇔ aᶜ = b. Brzmi skomplikowanie? Wcale nie! W praktyce logarytm to po prostu pytanie: "Do jakiej potęgi należy podnieść liczbę a, żeby otrzymać liczbę b?".

Spójrzmy na przykład: log₂8 = 3, ponieważ 2³ = 8. Widzisz? Pytamy: "Do jakiej potęgi muszę podnieść 2, żeby otrzymać 8?". Odpowiedź to 3, bo 2 razy 2 razy 2 (czyli 2 do potęgi 3) daje 8. Proste, prawda?

Krok po kroku: jak czytać zapis "logₐb = c" i nie zwariować?

Rozłóżmy ten zapis na czynniki pierwsze, żebyś dokładnie wiedział, co jest czym:

1. a (podstawa logarytmu): To liczba, którą będziemy podnosić do potęgi. Zawsze jest zapisana małą czcionką u dołu symbolu "log". Pomyśl o niej jak o "bazie" twojej potęgi.
2. b (liczba logarytmowana): To wynik, który chcemy uzyskać po podniesieniu podstawy do potęgi. To ta większa liczba obok "log". To jest "cel", do którego dążymy.
3. c (wynik logarytmu): To wykładnik potęgi, którego szukamy. To jest odpowiedź na nasze pytanie "do jakiej potęgi?".

Logarytm dla każdego: zrozum podstawy i nie bój się!

Zrozumienie logarytmów sprowadza się do jednej prostej zasady, którą powtórzę do znudzenia: to odwrotność potęgowania. Jeśli rozumiesz potęgi, zrozumiesz i logarytmy. Nie ma tu żadnej magii ani czarnej dziury, tylko inna perspektywa na to samo działanie. To jakbyś miał trzy liczby: podstawę, wykładnik i wynik. Potęgowanie pyta: "Jaki będzie wynik, jeśli podniosę podstawę do wykładnika?". Logarytm pyta: "Jaki jest wykładnik, jeśli znam podstawę i wynik?".

Zrozumieć logarytm w 30 sekund: potęgowanie na opak

Pomyśl o tym tak: tak jak odejmowanie jest odwrotnością dodawania (2+3=5, więc 5-3=2), a dzielenie jest odwrotnością mnożenia (2*3=6, więc 6/3=2), tak logarytm jest odwrotnością potęgowania. Kiedy masz potęgę, np. 2³ = 8, znasz podstawę (2), wykładnik (3) i wynik (8). Logarytm pozwala ci znaleźć wykładnik, gdy znasz podstawę i wynik. To naprawdę jest "potęgowanie na opak"!

Jakie trzy warunki muszą być spełnione, żeby logarytm miał sens? (a > 0, a ≠ 1, b > 0)

Żeby logarytm "działał" poprawnie i miał sens, musimy spełnić trzy proste warunki. Nie są one tam bez powodu, a ich zrozumienie pomoże Ci uniknąć błędów:

• Podstawa a > 0: Podstawa logarytmu, czyli nasze "a", musi być liczbą dodatnią. Dlaczego? Bo gdyby podstawa była ujemna (np. (-2)³ = -8, ale (-2)² = 4), to podnoszenie jej do różnych potęg raz dawałoby wynik dodatni, raz ujemny. To sprawiłoby, że logarytm nie miałby jednoznacznej wartości, a to w matematyce jest problemem.
• Podstawa a ≠ 1: Podstawa logarytmu nie może być równa 1. Zastanów się: 1 podniesione do dowolnej potęgi zawsze daje 1 (1²=1, 1⁵⁰=1). Gdyby podstawa była 1, to logarytm z 1 o podstawie 1 byłby nieokreślony (bo 1 do dowolnej potęgi daje 1), a logarytm z innej liczby (np. log₁5) byłby niemożliwy do obliczenia, bo nigdy nie dostaniemy 5 podnosząc 1 do jakiejkolwiek potęgi.
• Liczba logarytmowana b > 0: Liczba logarytmowana, czyli nasze "b", musi być zawsze dodatnia. To bardzo ważne! Jeśli masz dodatnią podstawę (a > 0), to niezależnie od tego, do jakiej potęgi ją podniesiesz (czy to potęga dodatnia, ujemna, ułamkowa), wynik zawsze będzie liczbą dodatnią. Nigdy nie otrzymasz zera ani liczby ujemnej. Dlatego logarytm z liczby ujemnej lub zera po prostu nie istnieje!

Proste przykłady, które od razu zrozumiesz (log₂8, log₁₀100)

Przećwiczmy to na kilku przykładach. Pamiętaj o pytaniu: "Do jakiej potęgi muszę podnieść podstawę, żeby otrzymać liczbę logarytmowaną?".

1. log₂8: Pytamy: "Do jakiej potęgi muszę podnieść 2, żeby otrzymać 8?". Odpowiedź: 2³ = 8, więc log₂8 = 3.
2. log₁₀100: Pytamy: "Do jakiej potęgi muszę podnieść 10, żeby otrzymać 100?". Odpowiedź: 10² = 100, więc log₁₀100 = 2.
3. log₃9: Pytamy: "Do jakiej potęgi muszę podnieść 3, żeby otrzymać 9?". Odpowiedź: 3² = 9, więc log₃9 = 2.

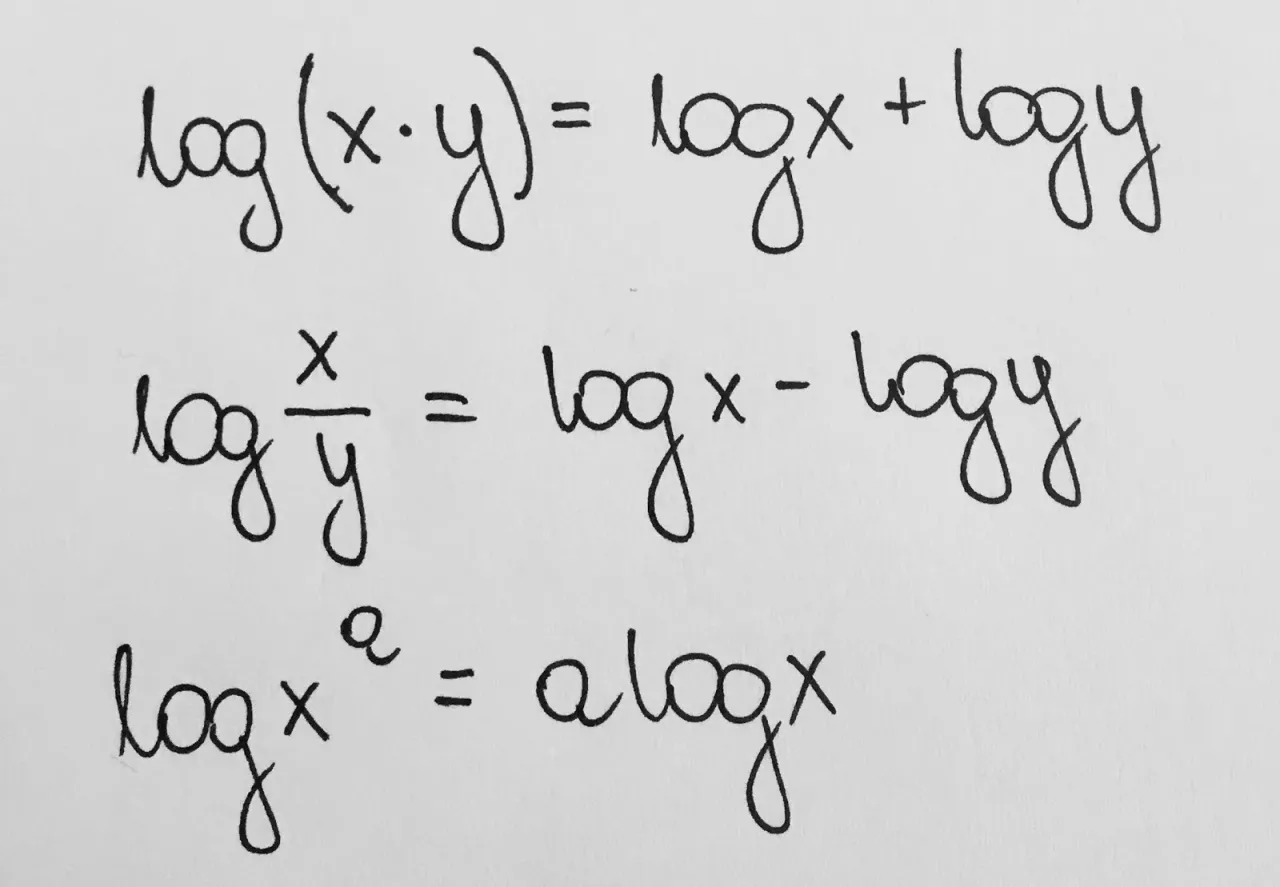
Twoja skrzynka narzędziowa: podstawowe wzory na logarytmy

Logarytmy, podobnie jak inne działania matematyczne, mają swoje "narzędzia" wzory, które ułatwiają pracę i pozwalają upraszczać skomplikowane wyrażenia. Nie musisz ich wkuwać na pamięć od razu, ale zrozumienie, jak działają, otworzy Ci drzwi do rozwiązywania bardziej złożonych zadań. Skupimy się na trzech najważniejszych, które są Twoimi najlepszymi przyjaciółmi.

Wzór nr 1: Logarytm z mnożenia (iloczynu) - jak go używać?

Ten wzór mówi, że logarytm z iloczynu (czyli mnożenia) dwóch liczb można rozbić na sumę logarytmów tych liczb. To bardzo przydatne, gdy masz do czynienia z dużymi liczbami w logarytmie. Wzór wygląda tak: logₐ(x * y) = logₐx + logₐy.

Przykład: Obliczmy log₂(4 * 8). Zamiast najpierw mnożyć 4 * 8 = 32 i potem liczyć log₂32 (co też da się zrobić, bo 2⁵=32), możemy użyć wzoru: log₂(4 * 8) = log₂4 + log₂8. Wiemy, że log₂4 = 2 (bo 2²=4) i log₂8 = 3 (bo 2³=8). Zatem log₂(4 * 8) = 2 + 3 = 5. Jak widać, wynik jest ten sam, a czasem takie rozbicie bardzo ułatwia sprawę!

Wzór nr 2: Logarytm z dzielenia (ilorazu) - kiedy się przydaje?

Podobnie jak z mnożeniem, logarytm z ilorazu (czyli dzielenia) dwóch liczb można rozbić na różnicę logarytmów tych liczb. Wzór to: logₐ(x / y) = logₐx - logₐy.

Przykład: Obliczmy log₂(8 / 4). Używając wzoru: log₂(8 / 4) = log₂8 - log₂4. Wiemy, że log₂8 = 3 i log₂4 = 2. Zatem log₂(8 / 4) = 3 - 2 = 1. Sprawdźmy: 8 / 4 = 2, a log₂2 = 1 (bo 2¹=2). Zgadza się!

Wzór nr 3: Logarytm z potęgi - Twój najlepszy przyjaciel w upraszczaniu

Ten wzór jest absolutnie genialny i często ratuje życie! Mówi on, że jeśli liczba logarytmowana jest podniesiona do jakiejś potęgi, to ten wykładnik potęgi możesz "wyrzucić" przed logarytm jako mnożnik. Wzór: logₐ(xⁿ) = n * logₐx.

Przykład: Obliczmy log₂(8²). Zamiast liczyć 8² = 64 i potem log₂64 (co daje 6, bo 2⁶=64), możemy użyć wzoru: log₂(8²) = 2 * log₂8. Wiemy, że log₂8 = 3. Zatem 2 * 3 = 6. To naprawdę upraszcza obliczenia, zwłaszcza gdy wykładniki są duże!

Przykłady obliczeniowe z użyciem każdego ze wzorów

Teraz połączmy te wzory w praktyce. Zobaczysz, jak bardzo ułatwiają życie!

1. Oblicz log₃(9 * 27):
   • Krok 1: Użyj wzoru na logarytm iloczynu: log₃9 + log₃27.
   • Krok 2: Oblicz poszczególne logarytmy: log₃9 = 2 (bo 3²=9), log₃27 = 3 (bo 3³=27).
   • Krok 3: Dodaj wyniki: 2 + 3 = 5.
2. Oblicz log₅(125 / 5):
   • Krok 1: Użyj wzoru na logarytm ilorazu: log₅125 - log₅5.
   • Krok 2: Oblicz poszczególne logarytmy: log₅125 = 3 (bo 5³=125), log₅5 = 1 (bo 5¹=5).
   • Krok 3: Odejmij wyniki: 3 - 1 = 2.
3. Uprość log₂(16³):
   • Krok 1: Użyj wzoru na logarytm potęgi: 3 * log₂16.
   • Krok 2: Oblicz log₂16 = 4 (bo 2⁴=16).
   • Krok 3: Pomnóż: 3 * 4 = 12.

Logarytmy specjalne: dziesiętny, naturalny i ich tajemnice

W świecie logarytmów są też takie, które spotkasz częściej niż inne i które mają swoje specjalne, skrócone oznaczenia. Warto je znać, bo pojawiają się wszędzie od chemii po finanse.

Co to jest logarytm dziesiętny (log)? Dlaczego nie ma zapisanej podstawy?

Logarytm dziesiętny to po prostu logarytm, którego podstawą jest liczba 10. Jest tak powszechny, że zazwyczaj nie zapisujemy tej dziesiątki u dołu. Jeśli widzisz "log" bez żadnej liczby w indeksie dolnym, to wiedz, że chodzi o podstawę 10. Przykład: log(100) = 2, bo 10² = 100.

Czym jest logarytm naturalny (ln) i tajemnicza liczba "e"?

Logarytm naturalny to logarytm o bardzo szczególnej podstawie, którą jest liczba "e". Liczba "e" to jedna z najważniejszych stałych matematycznych (obok pi, czyli π). Jej wartość to w przybliżeniu 2,718. Logarytm naturalny oznaczamy jako "ln". Nie będziemy wchodzić w szczegóły, skąd się bierze "e", ale wiedz, że jest kluczowa w wielu dziedzinach nauki i ekonomii.

Jakie są dwie "magiczne" tożsamości? (logₐa = 1 i logₐ1 = 0)

Są dwie bardzo proste i niezwykle przydatne "tożsamości" logarytmiczne, które wynikają wprost z definicji potęgowania:

• logₐa = 1: Zawsze, gdy podstawa logarytmu i liczba logarytmowana są takie same, wynik to 1. Dlaczego? Bo a podniesione do potęgi 1 daje a (a¹ = a). Np. log₅5 = 1, bo 5¹ = 5.
• logₐ1 = 0: Zawsze, gdy liczba logarytmowana to 1, wynik logarytmu to 0 (niezależnie od podstawy!). Dlaczego? Bo każda liczba (różna od zera) podniesiona do potęgi 0 daje 1 (a⁰ = 1). Np. log₇1 = 0, bo 7⁰ = 1.

Pułapki i błędy: jak ich unikać i zdobywać punkty?

Każdy, kto uczy się logarytmów, popełnia podobne błędy. Ale dobra wiadomość jest taka, że jeśli wiesz, na co uważać, możesz ich łatwo unikać. Pokażę Ci trzy najczęstsze pułapki.

Błąd #1: Mylenie podstawy z liczbą logarytmowaną

To klasyka! Początkujący często mylą, która liczba jest podstawą, a która liczbą logarytmowaną. Na przykład, mylą log₂8 z log₈2. Pamiętaj: podstawa jest zawsze mała i na dole! log₂8 to pytanie "2 do jakiej potęgi da 8?" (odpowiedź: 3). Natomiast log₈2 to pytanie "8 do jakiej potęgi da 2?" (odpowiedź: 1/3, bo 8 do potęgi 1/3 to pierwiastek sześcienny z 8, czyli 2). Widzisz, jak różne są wyniki? Zawsze zwracaj uwagę na położenie liczb!

Błąd #2: "Na kreatywności" - czyli niepoprawne rozbijanie logarytmu z sumy

To bardzo ważna zasada: NIE ISTNIEJE wzór na logarytm z sumy! Wielu uczniów, widząc wzór na logarytm iloczynu (log(x*y) = log(x) + log(y)), próbuje "na siłę" stworzyć podobny wzór dla sumy, np. log(x+y) = log(x) + log(y). To jest ABSOLUTNIE BŁĘDNE! NIE RÓB TAK! Logarytm z sumy nie da się tak po prostu rozbić. Pamiętaj, że wzory dotyczą tylko iloczynów, ilorazów i potęg.

Błąd #3: Zapominanie o dziedzinie - dlaczego liczba logarytmowana musi być dodatnia?

Przypomnij sobie warunek, że liczba logarytmowana (b) musi być zawsze większa od zera (b > 0). To jest kluczowe! Jeśli w zadaniu wyjdzie Ci, że masz obliczyć logarytm z liczby ujemnej lub zera, to znaczy, że albo popełniłeś błąd w obliczeniach, albo logarytm po prostu nie istnieje (jest "nieokreślony"). Pamiętaj, że dodatnia podstawa podniesiona do dowolnej potęgi ZAWSZE da wynik dodatni. Nie da się "wytworzyć" zera ani liczby ujemnej w ten sposób.

Zmień myślenie o logarytmach i zobacz, jakie są proste!

Kluczem do sukcesu z logarytmami jest zmiana sposobu myślenia o nich. Przestań postrzegać je jako coś obcego i przerażającego, a zacznij traktować jak inną formę zadawania pytań o potęgi. To naprawdę działa!

Technika zadawania pytania: "Do jakiej potęgi muszę podnieść. .. ?"

Wzmocnijmy tę technikę, bo jest ona Twoim najlepszym przyjacielem. Zawsze, gdy widzisz logarytm, zadaj sobie to proste pytanie. Spróbujmy razem, spróbuj rozwiązać w głowie:

• log₄16? Pytanie: "Do jakiej potęgi muszę podnieść 4, żeby otrzymać 16?". Odpowiedź: 2 (bo 4²=16).
• log₅25? Pytanie: "Do jakiej potęgi muszę podnieść 5, żeby otrzymać 25?". Odpowiedź: 2 (bo 5²=25).
• log₁₀1000? Pytanie: "Do jakiej potęgi muszę podnieść 10, żeby otrzymać 1000?". Odpowiedź: 3 (bo 10³=1000).

Widzisz, jakie to proste, gdy tylko zmienisz perspektywę?

Przeczytaj również: Jak obliczyć błąd bezwzględny i względny? Przewodnik krok po kroku

Przekształcanie logarytmów na potęgi: ćwiczenia, które budują intuicję

Ćwiczenie czyni mistrza! Poniżej znajdziesz kilka prostych ćwiczeń. Spróbuj je rozwiązać, a potem sprawdź rozwiązania. To świetnie buduje intuicję.

Ćwiczenia: Zamień logarytm na potęgę:

1. log₅25 = 2 (Rozwiązanie: 5² = 25)
2. log₁₀1000 = 3 (Rozwiązanie: 10³ = 1000)

Ćwiczenia: Zamień potęgę na logarytm:

1. 2⁴ = 16 (Rozwiązanie: log₂16 = 4)
2. 3¹ = 3 (Rozwiązanie: log₃3 = 1)

Dlaczego logarytmy są przydatne? Krótkie spojrzenie na skalę pH i decybele

Możesz się zastanawiać: "Po co mi to wszystko?". Logarytmy są niezwykle przydatne w wielu dziedzinach nauki i życia codziennego, zwłaszcza gdy mamy do czynienia z bardzo dużymi lub bardzo małymi liczbami. Pomagają nam "upchnąć" ogromne zakresy wartości w bardziej zrozumiałe skale. Oto kilka przykładów:

• Skala pH: Używana w chemii do określania kwasowości lub zasadowości roztworów. Zamiast operować na bardzo małych stężeniach jonów wodorowych (np. 0,0000001 M), dzięki logarytmom mamy prostą skalę od 0 do 14. Dużo wygodniej, prawda?
• Decybele (dB): Mierzą głośność dźwięku. Ludzkie ucho jest w stanie słyszeć dźwięki o ogromnej rozpiętości intensywności. Skala logarytmiczna pozwala na wygodne przedstawienie tej różnicy, sprawiając, że różnica między szeptem a startującym odrzutowcem jest mierzalna na prostej skali.
• Skala Richtera: Służy do mierzenia siły trzęsień ziemi. Każdy kolejny stopień na skali oznacza dziesięciokrotnie większą amplitudę drgań. Dzięki logarytmom, trzęsienie ziemi o sile 7 w skali Richtera jest dziesięć razy silniejsze niż to o sile 6, a nie tylko o jeden "punkt" silniejsze.