Dzielenie pisemne z przecinkiem: Opanuj je raz na zawsze!

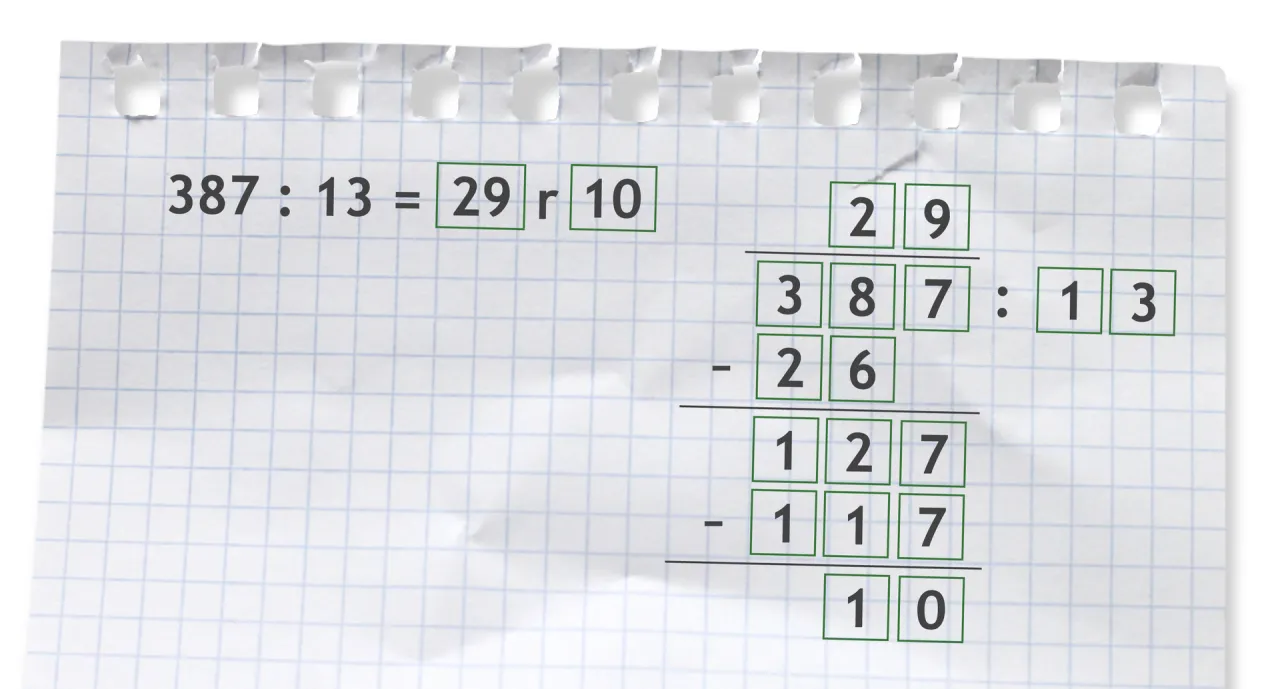
Dzielenie pisemne z przecinkiem: dlaczego bywa trudne i jak je opanować?

Wielu z nas, w tym i ja, na początku swojej przygody z matematyką miało pewne obawy przed dzieleniem pisemnym z przecinkiem. To prawda, że bywa ono wyzwaniem, zwłaszcza gdy pojawia się kwestia zarządzania przecinkiem dziesiętnym. Ale chcę Cię zapewnić, że jest to umiejętność, którą każdy może opanować. Cały sekret tkwi w zrozumieniu kilku prostych zasad, które postaram się rozłożyć na czynniki pierwsze w tym artykule.

Krótkie wprowadzenie: zrozumieć problem, by go rozwiązać

Z mojego doświadczenia wynika, że zrozumienie, z czym właściwie mamy problem, to już połowa sukcesu. Dzielenie pisemne z przecinkiem jest standardowym elementem edukacji matematycznej i jego opanowanie jest absolutnie fundamentalne. To nie tylko mechaniczne wykonywanie działań, ale także rozwijanie logicznego myślenia i precyzji, które przydają się w wielu innych dziedzinach.

Kiedy ta umiejętność przydaje się w prawdziwym życiu?

Możesz myśleć, że to tylko szkolna teoria, ale nic bardziej mylnego! Dzielenie pisemne z przecinkiem ma mnóstwo praktycznych zastosowań w codziennym życiu. Wyobraź sobie, że musisz obliczyć średnią cenę za kilogram produktu, gdy znasz cenę opakowania i jego wagę. Albo gdy dzielisz rachunek ze znajomymi w restauracji. Przydaje się też przy przeliczaniu walut, planowaniu budżetu, czy nawet przy prostych przepisach kulinarnych, gdy trzeba proporcjonalnie zmniejszyć lub zwiększyć składniki. To naprawdę uniwersalna umiejętność!

Pierwszy krok: dzielenie liczby dziesiętnej przez liczbę całkowitą

Zacznijmy od najprostszego wariantu, który stanowi świetną bazę do dalszych, bardziej złożonych przypadków. Dzielenie liczby dziesiętnej przez liczbę całkowitą jest bardzo podobne do dzielenia liczb naturalnych, z jedną kluczową różnicą umiejscowieniem przecinka.

Krok po kroku na przykładzie: Jak podzielić 8, 4 przez 2?

Przyjrzyjmy się temu na konkretnym przykładzie. Chcemy podzielić 8,4 przez 2. Wykonujemy to niemal identycznie jak dzielenie liczb naturalnych:

1. Ustawienie: Zapisz działanie w formie dzielenia pisemnego, czyli "pod kreską".
2. Dzielenie części całkowitej: Zacznij dzielić od lewej strony. Ile razy 2 mieści się w 8? Cztery razy. Wpisz 4 w wyniku.
3. Przecinek: W tym momencie napotykamy przecinek w dzielnej (8,4). To jest ten kluczowy moment! Musisz natychmiast postawić przecinek w wyniku, dokładnie nad przecinkiem w dzielnej.
4. Dzielenie części dziesiętnej: Teraz sprowadź kolejną cyfrę z dzielnej (4) obok reszty (w tym przypadku reszta z 8:2 to 0, więc po prostu sprowadzasz 4). Ile razy 2 mieści się w 4? Dwa razy. Wpisz 2 w wyniku, po przecinku.
5. Wynik: Otrzymujemy 4,2.

Kluczowy moment: Gdzie i kiedy postawić przecinek w wyniku?

Jak wspomniałem, to absolutnie najważniejsza zasada w tym wariancie: przecinek w wyniku stawiamy dokładnie nad przecinkiem w dzielnej, w momencie, gdy przechodzimy do dzielenia cyfr znajdujących się po przecinku w dzielnej. Nie ma tu miejsca na zgadywanie czy przesuwanie po prostu "przenosisz" go w górę.

Ćwiczenie praktyczne z rozwiązaniem: Sprawdź się na działaniu 12, 69: 3

Spróbujmy teraz z nieco dłuższym przykładem, aby utrwalić tę zasadę:

1. Ustawienie: Zapisz 12,69 : 3 pod kreską.
2. Dzielenie części całkowitej: Ile razy 3 mieści się w 12? Cztery razy. Wpisz 4 w wyniku.
3. Przecinek: Po 12 jest przecinek, więc natychmiast postaw przecinek w wyniku, nad przecinkiem w dzielnej.
4. Dzielenie pierwszej cyfry po przecinku: Sprowadź 6. Ile razy 3 mieści się w 6? Dwa razy. Wpisz 2 w wyniku, po przecinku.
5. Dzielenie drugiej cyfry po przecinku: Sprowadź 9. Ile razy 3 mieści się w 9? Trzy razy. Wpisz 3 w wyniku.
6. Wynik: Otrzymujemy 4,23.

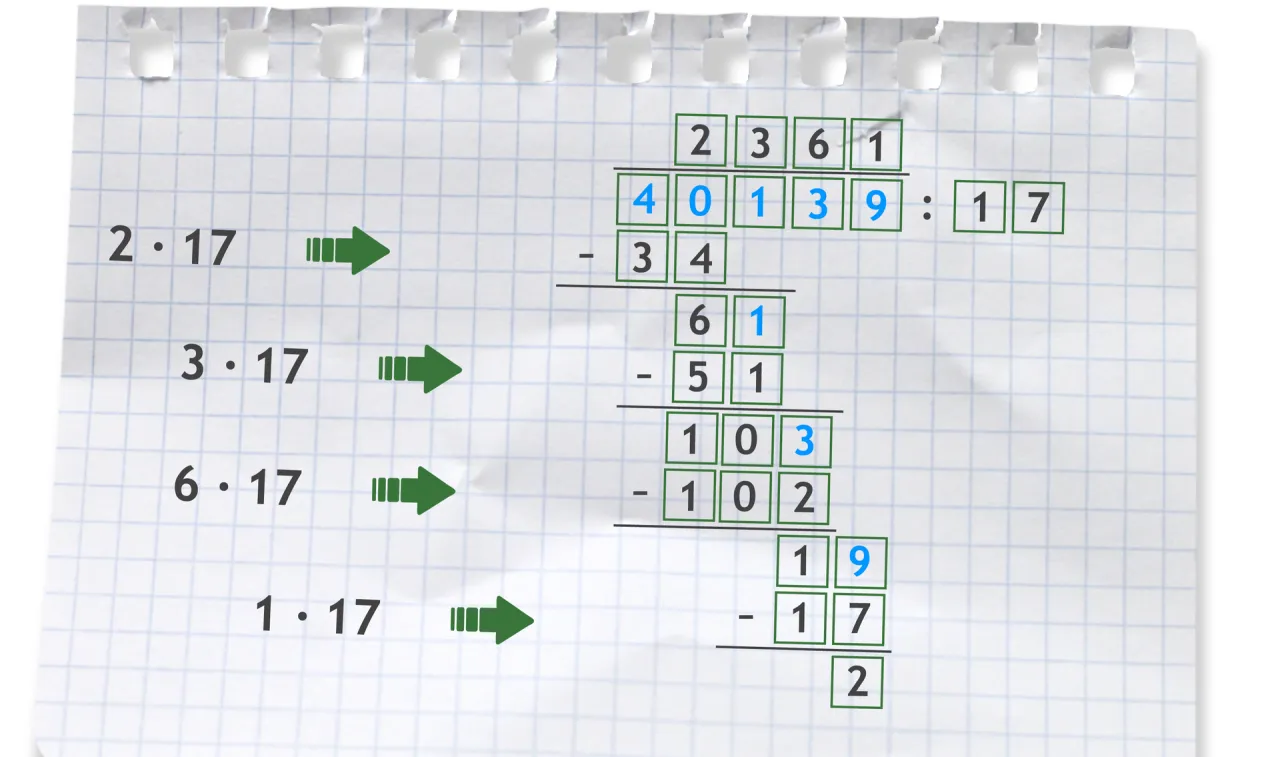
Dzielnik z przecinkiem? Pozbądź się go sprytnym trikiem!

Teraz przechodzimy do wariantu, który bywa nieco bardziej podchwytliwy: dzielenie, gdy to dzielnik jest liczbą dziesiętną. Ale spokojnie, mam dla Ciebie prosty i skuteczny trik, który uprości całe działanie do formy, którą już znasz.

Najważniejsza reguła: "rozszerzanie" ułamka, czyli przesuwanie przecinka

Kluczem do sukcesu jest pozbycie się przecinka z dzielnika. Jak to zrobić? Musimy "rozszerzyć" ułamek, czyli pomnożyć zarówno dzielną, jak i dzielnik przez tę samą potęgę liczby 10 (czyli przez 10, 100, 1000 itd.), tak aby dzielnik stał się liczbą całkowitą. To jest jak mnożenie licznika i mianownika ułamka przez tę samą liczbę wartość ułamka się nie zmienia, a nam jest łatwiej liczyć.

Instrukcja krok po kroku: Dzielimy 9, 75 przez 0, 5

Weźmy na warsztat przykład 9,75 : 0,5:

1. Cel: Chcemy, aby 0,5 stało się liczbą całkowitą. Aby to osiągnąć, musimy przesunąć przecinek o jedno miejsce w prawo. To oznacza pomnożenie przez 10.
2. Przesunięcie przecinka w dzielniku: 0,5 * 10 = 5.
3. Przesunięcie przecinka w dzielnej: Pamiętaj, co robisz z dzielnikiem, musisz zrobić i z dzielną! 9,75 * 10 = 97,5.
4. Nowe działanie: Nasze działanie 9,75 : 0,5 zamienia się na 97,5 : 5.
5. Wykonanie dzielenia: Teraz wykonaj dzielenie 97,5 : 5 jak w poprzednich przykładach (liczba dziesiętna przez całkowitą).
   • Ile razy 5 w 9? Raz (1 * 5 = 5, reszta 4).
   • Sprowadź 7. Mamy 47. Ile razy 5 w 47? Dziewięć razy (9 * 5 = 45, reszta 2).
   • Postaw przecinek w wyniku (nad przecinkiem w 97,5).
   • Sprowadź 5. Mamy 25. Ile razy 5 w 25? Pięć razy (5 * 5 = 25, reszta 0).
6. Wynik: Otrzymujemy 19,5.

O czym absolutnie nie możesz zapomnieć? (przesunięcie przecinka w obu liczbach)

To jest najczęstszy błąd, jaki widzę! Uczniowie często pamiętają o przesunięciu przecinka w dzielniku, ale zapominają o tym samym w dzielnej. To tak, jakbyś zmieniał wartość tylko jednej strony równania wynik będzie błędny. Zawsze pamiętaj: co robisz z dzielnikiem, musisz zrobić z dzielną!

Trudniejszy przykład: Co zrobić, gdy w dzielniku jest więcej miejsc po przecinku (np. 4, 5: 0, 15)?

1. Cel: Chcemy, aby 0,15 stało się liczbą całkowitą. Musimy przesunąć przecinek o dwa miejsca w prawo, czyli pomnożyć przez 100.
2. Przesunięcie przecinka w dzielniku: 0,15 * 100 = 15.
3. Przesunięcie przecinka w dzielnej: Musimy pomnożyć 4,5 przez 100. Przesuwamy przecinek o dwa miejsca w prawo. Po jednym miejscu (za 5) musimy dopisać zero. Tak więc 4,5 * 100 = 450.
4. Nowe działanie: Nasze działanie 4,5 : 0,15 zamienia się na 450 : 15.
5. Wykonanie dzielenia:
   • Ile razy 15 w 45? Trzy razy (3 * 15 = 45, reszta 0).
   • Sprowadź 0. Ile razy 15 w 0? Zero razy. Wpisz 0 w wyniku.
6. Wynik: Otrzymujemy 30.

Co, jeśli zostaje reszta? Dzielenie "do skutku" z dopisywaniem zer

Często zdarza się, że dzielenie nie kończy się od razu, a po podzieleniu części całkowitej lub po kilku cyfrach po przecinku, nadal zostaje reszta. W takich sytuacjach, aby kontynuować obliczenia i uzyskać dokładniejszy wynik, dopisujemy zera.

Praktyczny przykład: Jak zamienić ułamek zwykły na dziesiętny dzieleniem (np. 1: 4)?

To świetny sposób na zrozumienie dopisywania zer. Jak zamienić 1/4 na ułamek dziesiętny? To nic innego, jak podzielenie 1 przez 4:

1. Ustawienie: Zapisz 1 : 4 pod kreską.
2. Dzielenie: Ile razy 4 mieści się w 1? Zero razy. Wpisz 0 w wyniku.
3. Przecinek i zero: Po 1 nie ma już cyfr, ale chcemy kontynuować. Więc stawiamy przecinek w wyniku (po 0) i dopisujemy zero do 1, otrzymując 10.
4. Kontynuacja dzielenia: Ile razy 4 mieści się w 10? Dwa razy (2 * 4 = 8, reszta 2). Wpisz 2 w wyniku, po przecinku.
5. Kolejne zero: Została reszta 2. Dopisujemy kolejne zero (możemy to robić po przecinku bez ograniczeń, aż do uzyskania reszty 0 lub wyniku okresowego). Mamy 20.
6. Dalsze dzielenie: Ile razy 4 mieści się w 20? Pięć razy (5 * 4 = 20, reszta 0). Wpisz 5 w wyniku.
7. Wynik: Otrzymujemy 0,25.

Sekret dopisywania zer w dzielnej jak i kiedy to robić legalnie?

Sekret jest prosty: po tym, jak postawisz przecinek w wyniku (bo skończyły Ci się cyfry w części całkowitej lub po prostu chcesz kontynuować dzielenie po przecinku), możesz dopisywać zera do reszty w dzielnej. To jest całkowicie "legalne" matematycznie, ponieważ dopisywanie zer na końcu liczby dziesiętnej nie zmienia jej wartości (np. 7 = 7,0 = 7,00). Dzięki temu możesz kontynuować dzielenie, aż do uzyskania reszty zero lub stwierdzenia, że wynik jest okresowy.

Krok po kroku: Dzielimy 7 przez 2, uzyskując wynik z przecinkiem

Spróbujmy podzielić 7 przez 2:

1. Ustawienie: Zapisz 7 : 2 pod kreską.
2. Dzielenie części całkowitej: Ile razy 2 mieści się w 7? Trzy razy (3 * 2 = 6, reszta 1). Wpisz 3 w wyniku.
3. Przecinek i zero: Została reszta 1. Chcemy kontynuować, więc stawiamy przecinek w wyniku (po 3) i dopisujemy zero do reszty 1, tworząc 10.
4. Kontynuacja dzielenia: Ile razy 2 mieści się w 10? Pięć razy (5 * 2 = 10, reszta 0). Wpisz 5 w wyniku, po przecinku.
5. Wynik: Otrzymujemy 3,5.

Pułapki i błędy: czego unikać w dzieleniu pisemnym z przecinkiem?

Podczas nauki każdej nowej umiejętności, zwłaszcza matematycznej, łatwo o błędy. Z mojego doświadczenia wiem, że świadomość najczęstszych pułapek pozwala ich unikać. Przyjrzyjmy się im, abyś mógł ich świadomie unikać.

Błąd #1: Zgubiony lub źle postawiony przecinek w wyniku

To chyba najczęstszy i najbardziej kosztowny błąd. Zapomnienie o przecinku lub postawienie go w złym miejscu całkowicie zmienia wartość wyniku. Pamiętaj o zasadzie: gdy w dzielnej dochodzisz do przecinka, natychmiast postaw go w wyniku.
Błędnie: 8,4 : 2 = 42 (przecinek zgubiony)
Poprawnie: 8,4 : 2 = 4,2

Błąd #2: Przesunięcie przecinka tylko w jednej liczbie

Gdy dzielnik jest liczbą dziesiętną, absolutnie kluczowe jest przesunięcie przecinka zarówno w dzielniku, jak i w dzielnej o tę samą liczbę miejsc. Jeśli przesuniesz go tylko w jednej liczbie, zmienisz wartość całego działania. Przypomnij sobie zasadę "rozszerzania" ułamka mnożymy obie liczby przez tę samą potęgę 10.

Błąd #3: Pomyłki w odejmowaniu i mnożeniu w trakcie

Wyjątkowe sytuacje: co warto wiedzieć, by nic Cię nie zaskoczyło?

Matematyka potrafi zaskoczyć, ale z odpowiednią wiedzą żadna sytuacja nie będzie dla Ciebie problemem. Oto kilka mniej typowych, ale ważnych przypadków, które warto znać.

Gdy dzielna jest mniejsza od dzielnika (np. 3: 6)

Co zrobić, gdy liczba, którą dzielimy, jest mniejsza od dzielnika? To nic nadzwyczajnego, po prostu wynik będzie mniejszy niż 1. Zobaczmy na przykładzie 3 : 6:

1. Ustawienie: Zapisz 3 : 6 pod kreską.
2. Dzielenie: Ile razy 6 mieści się w 3? Zero razy. Wpisz 0 w wyniku.
3. Przecinek i zero: Po 3 nie ma już cyfr. Stawiamy przecinek w wyniku (po 0) i dopisujemy zero do 3, otrzymując 30.
4. Kontynuacja dzielenia: Ile razy 6 mieści się w 30? Pięć razy (5 * 6 = 30, reszta 0). Wpisz 5 w wyniku, po przecinku.
5. Wynik: Otrzymujemy 0,5.

Gdy w wyniku pojawiają się zera (np. 8, 16: 8)

Czasami po przecinku w wyniku pojawiają się zera. To normalne i nie należy się tym martwić. Zobaczmy na przykładzie 8,16 : 8:

1. Ustawienie: Zapisz 8,16 : 8 pod kreską.
2. Dzielenie części całkowitej: Ile razy 8 mieści się w 8? Raz. Wpisz 1 w wyniku.
3. Przecinek: Po 8 jest przecinek, więc postaw przecinek w wyniku (po 1).
4. Dzielenie pierwszej cyfry po przecinku: Sprowadź 1. Ile razy 8 mieści się w 1? Zero razy. Wpisz 0 w wyniku, po przecinku.
5. Dzielenie drugiej cyfry po przecinku: Sprowadź 6. Mamy 16. Ile razy 8 mieści się w 16? Dwa razy. Wpisz 2 w wyniku.
6. Wynik: Otrzymujemy 1,02.

Dzielenie, które się nie kończy: jak rozpoznać i zapisać wynik okresowy (np. 2: 3)?

Nie każde dzielenie ma "ładny" koniec z resztą zero. Czasami, niezależnie od tego, ile zer dopiszemy, pewne cyfry lub grupy cyfr w reszcie zaczynają się powtarzać. Taki wynik nazywamy wynikiem okresowym. Rozpoznasz go po tym, że w kolejnych krokach dzielenia pojawiają się te same reszty, co prowadzi do powtarzania się cyfr w wyniku. Aby zapisać taki wynik, powtarzającą się część (okres) umieszczamy w nawiasie. Na przykładzie 2 : 3:

1. 2 : 3 = 0,
2. Dopisujemy zero do 2 (mamy 20), w wyniku stawiamy przecinek.
3. 20 : 3 = 6 (6 * 3 = 18, reszta 2). Wpisujemy 6 w wyniku.
4. Dopisujemy zero do reszty 2 (mamy 20).
5. 20 : 3 = 6 (6 * 3 = 18, reszta 2). Wpisujemy kolejne 6 w wyniku.

Widzisz, reszta 2 i cyfra 6 w wyniku powtarzają się. Zapisujemy to jako 0,(6).

Podsumowanie: złote zasady dzielenia pisemnego z przecinkiem

Mam nadzieję, że ten przewodnik rozwiał Twoje wątpliwości dotyczące dzielenia pisemnego z przecinkiem. To umiejętność, która wymaga praktyki, ale z solidnymi podstawami i świadomością pułapek, możesz ją opanować do perfekcji. Pamiętaj, że matematyka to nie tylko liczby, ale też logiczne myślenie!

Twoja ściągawka: 4 kroki do poprawnego wyniku w każdej sytuacji

• Krok 1: Pozbądź się przecinka z dzielnika. Jeśli dzielnik jest liczbą dziesiętną, przesuń przecinek w nim (i w dzielnej!) o tyle miejsc w prawo, aby stał się liczbą całkowitą.
• Krok 2: Postaw przecinek w wyniku. Gdy w dzielnej dojdziesz do przecinka, natychmiast postaw go w wyniku, dokładnie nad przecinkiem w dzielnej.
• Krok 3: Dopisuj zera, jeśli zostaje reszta. Po postawieniu przecinka w wyniku, możesz dopisywać zera do reszty w dzielnej, aby kontynuować dzielenie "do skutku".
• Krok 4: Bądź precyzyjny. Dokładnie wykonuj mnożenie i odejmowanie na każdym etapie algorytmu.

Przeczytaj również: Jak obliczyć błąd bezwzględny i względny? Przewodnik krok po kroku

Jak samodzielnie sprawdzać wyniki, by mieć 100% pewności?

Zawsze zachęcam do sprawdzania swoich wyników. To prosta i skuteczna metoda na upewnienie się, że wszystko jest poprawnie. Aby sprawdzić wynik dzielenia, wystarczy pomnożyć otrzymany wynik przez dzielnik. Jeśli wynik mnożenia jest równy dzielnej, to Twoje dzielenie jest poprawne! Na przykład, jeśli 9,75 : 0,5 = 19,5, to sprawdź: 19,5 * 0,5 = 9,75. Działa!