Rozwiązywanie układów równań liniowych może wydawać się skomplikowane, ale z odpowiednią metodą staje się znacznie prostsze. Metoda podstawiania to jeden z najbardziej intuicyjnych sposobów na uporanie się z tym matematycznym wyzwaniem, szczególnie gdy szukasz jasnego i praktycznego przewodnika krok po kroku.
Rozwiązywanie układu równań metodą podstawiania 5 kluczowych kroków do sukcesu
- Wyznacz jedną niewiadomą z wybranego równania, najlepiej z współczynnikiem 1 lub -1.
- Podstaw wyznaczone wyrażenie do drugiego równania, pamiętając o użyciu nawiasów.
- Rozwiąż powstałe równanie z jedną niewiadomą, wykonując bezbłędne obliczenia.
- Oblicz drugą niewiadomą, podstawiając uzyskany wynik do wzoru z pierwszego kroku.
- Sprawdź poprawność rozwiązania, wstawiając obie wartości do początkowych równań.
Metoda podstawiania: Twój matematyczny sprzymierzeniec
Układ równań liniowych z dwiema niewiadomymi to nic innego jak zestaw dwóch równań, w których występują te same dwie niewiadome, zazwyczaj oznaczane jako x i y. Celem jest znalezienie takiej pary liczb, która jednocześnie spełnia oba równania. Takie układy spotykamy często w zadaniach tekstowych, na przykład gdy chcemy obliczyć wiek dwóch osób na podstawie danych o ich sumie i różnicy lat, albo gdy liczymy liczbę monet o różnych nominałach w portfelu.
Metoda podstawiania jest, moim zdaniem, bardzo intuicyjna. Polega ona na tym, że z jednego równania "wyciągamy" jedną niewiadomą (np. x) i wyrażamy ją za pomocą drugiej niewiadomej (np. y). Następnie to wyrażenie podstawiamy do drugiego równania, co pozwala nam "pozbyć się" jednej niewiadomej i sprowadzić problem do prostszego równania z jedną niewiadomą. To sprawia, że jest to doskonały punkt wyjścia do nauki rozwiązywania układów równań, choć istnieją też inne metody, takie jak metoda przeciwnych współczynników czy metoda graficzna.Kiedy metoda podstawiania jest szczególnie efektywna? Z mojego doświadczenia wynika, że najlepiej sprawdza się, gdy w jednym z równań współczynnik przy jednej z niewiadomych wynosi 1 lub -1. Wtedy wyznaczenie tej niewiadomej jest niezwykle proste i pozwala uniknąć pracy z ułamkami, co zawsze jest plusem!
Fundamenty sukcesu: Jak przygotować się do rozwiązywania układów równań?
Zanim zagłębimy się w samą metodę podstawiania, musimy upewnić się, że masz solidne podstawy z przekształceń algebraicznych. To są fundamenty, bez których trudno o sukces. Pamiętaj o zasadach przenoszenia wyrazów z jednej strony równania na drugą ze zmianą znaku, a także o mnożeniu lub dzieleniu obu stron równania przez tę samą liczbę. Na przykład, jeśli masz równanie 2x + 3 = 7, to aby wyznaczyć x, najpierw przenosisz 3 na prawą stronę, zmieniając znak: 2x = 7 - 3, co daje 2x = 4. Następnie dzielisz obie strony przez 2, uzyskując x = 2.
Jak już wspomniałem, najlepiej jest wybrać równanie, w którym jedna z niewiadomych ma współczynnik 1 lub -1. Na przykład, w układzie:
x + 2y = 5
3x - y = 1
Zdecydowanie najłatwiej będzie wyznaczyć x z pierwszego równania lub y z drugiego. Wybierając x z pierwszego, dostajemy x = 5 - 2y. Proste, prawda?
Częstym błędem, który widzę u moich uczniów, są pomyłki w znakach przy przenoszeniu wyrazów. Weźmy przykład: jeśli masz -y + 4 = 2x i chcesz wyznaczyć y, to przeniesienie 4 na drugą stronę da -y = 2x - 4. Aby pozbyć się minusa przy y, musisz pomnożyć całe równanie przez -1, co da y = -2x + 4. Pamiętaj, że minus dotyczy wtedy każdego wyrazu po prawej stronie!
Metoda podstawiania w 5 prostych krokach: Przewodnik dla każdego
Krok 1: Wyznaczenie jednej niewiadomej
Pierwszy krok to wyznaczenie jednej niewiadomej z jednego z równań. Jak już wiemy, najlepiej jest wybrać takie równanie i taką niewiadomą, aby współczynnik przy niej wynosił 1 lub -1. Dzięki temu unikniemy ułamków, co znacznie uprości dalsze obliczenia. Na przykład, jeśli mamy układ:
1) x + 3y = 10
2) 2x - y = 5
Najłatwiej będzie wyznaczyć x z pierwszego równania: x = 10 - 3y. To jest nasz wzór, który wykorzystamy w kolejnym kroku.
Krok 2: Podstawienie wyrażenia do drugiego równania
Teraz podstawiamy wyznaczone wyrażenie do drugiego równania. To kluczowy moment! Jeśli wyznaczyłeś x, podstawiasz je do drugiego równania w miejsce x. I tutaj bardzo ważna uwaga: zawsze używaj nawiasów, gdy podstawiasz całe wyrażenie! Pominięcie nawiasów to jeden z najczęstszych błędów, prowadzący do pomyłek w mnożeniu. W naszym przykładzie, podstawiając x = 10 - 3y do drugiego równania 2x - y = 5, otrzymujemy: 2(10 - 3y) - y = 5. Widzisz, jak nawiasy chronią nas przed błędem?
Krok 3: Rozwiązanie równania z jedną niewiadomą
Po podstawieniu uzyskaliśmy równanie z tylko jedną niewiadomą. Teraz nadszedł czas, aby je rozwiązać. To standardowe równanie liniowe, które rozwiązujemy, stosując znane zasady: najpierw wykonujemy mnożenie (jeśli są nawiasy), następnie przenosimy wszystkie wyrazy z niewiadomą na jedną stronę, a liczby na drugą, pamiętając o zmianie znaków. Na koniec dzielimy obie strony przez współczynnik stojący przy niewiadomej. Kontynuując nasz przykład:
2(10 - 3y) - y = 5
20 - 6y - y = 5
20 - 7y = 5
-7y = 5 - 20
-7y = -15
y = -15 / -7
y = 15/7
Krok 4: Obliczenie drugiej niewiadomej
Mamy już wartość jednej niewiadomej (y = 15/7). Teraz musimy obliczyć drugą niewiadomą (x). W tym celu wracamy do wzoru, który wyznaczyliśmy w Kroku 1: x = 10 - 3y. To bardzo ważne, aby podstawić y właśnie do tego wzoru, a nie do jednego z początkowych równań to pozwala uniknąć dodatkowych, często zbędnych obliczeń.
Podstawiając y = 15/7:
x = 10 - 3 * (15/7)
x = 10 - 45/7
x = 70/7 - 45/7
x = 25/7
Przeczytaj również: Jak obliczyć błąd bezwzględny i względny? Przewodnik krok po kroku
Krok 5: Sprawdzenie rozwiązania
Ostatni krok jest opcjonalny, ale ja zawsze go polecam to sprawdzenie rozwiązania. Dzięki niemu możesz upewnić się, że nie popełniłeś żadnego błędu. Wstawiamy obie obliczone wartości (x = 25/7 i y = 15/7) do obu początkowych równań. Jeśli oba równania są spełnione (lewa strona równa się prawej), to masz pewność, że rozwiązanie jest poprawne.
Dla pierwszego równania x + 3y = 10:
25/7 + 3 * (15/7) = 25/7 + 45/7 = 70/7 = 10. Zgadza się!
Dla drugiego równania 2x - y = 5:
2 * (25/7) - 15/7 = 50/7 - 15/7 = 35/7 = 5. Zgadza się!
Rozwiązanie jest poprawne!
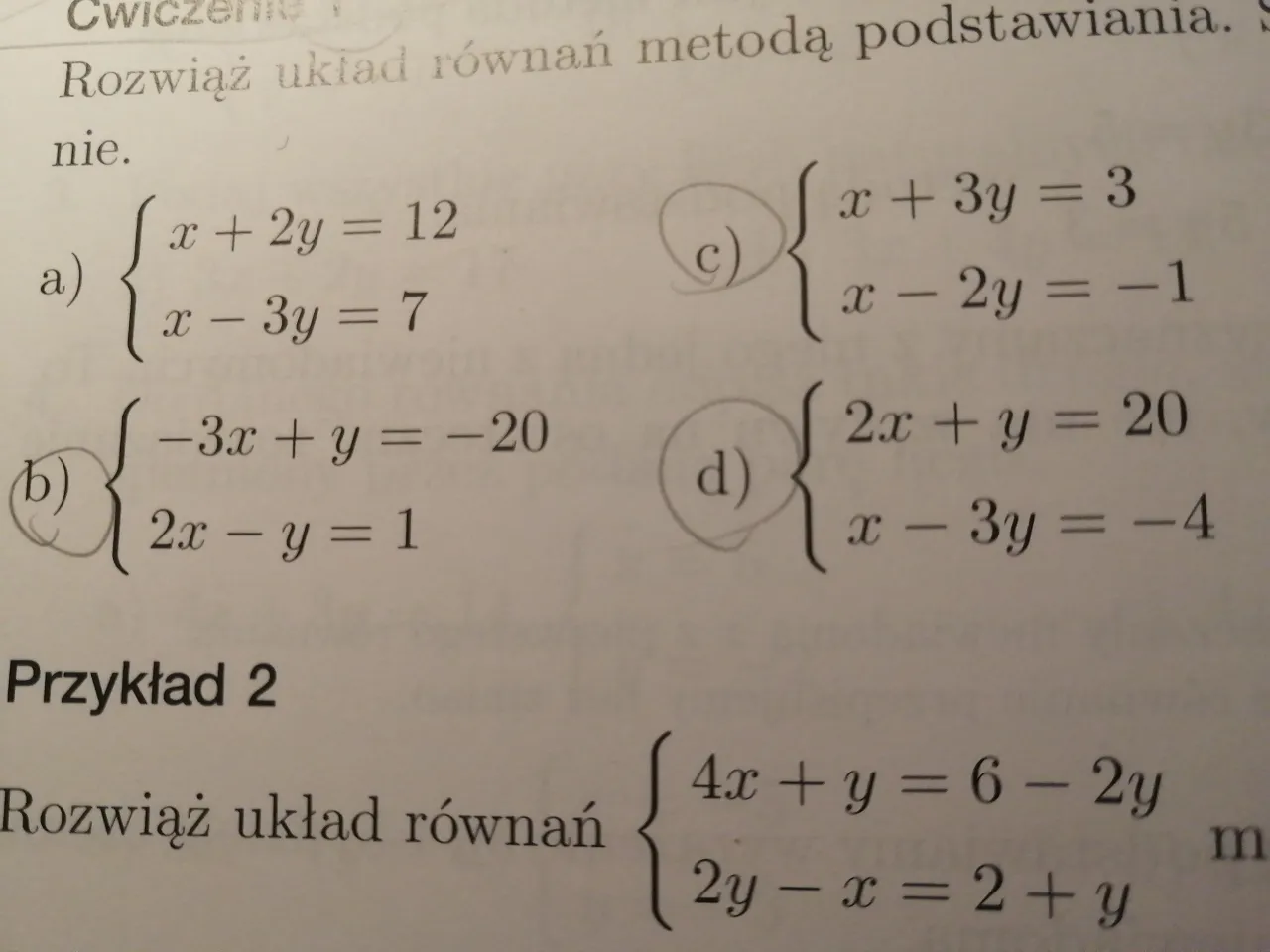
Przykład: Rozwiązujemy typowe zadanie krok po kroku
Wyobraź sobie, że masz następujący układ równań do rozwiązania:
1) 3x + y = 7
2) 5x - 2y = 1
Przeprowadźmy to krok po kroku, stosując metodę podstawiania.
-
Krok 1: Wyznaczamy jedną niewiadomą. Z pierwszego równania najłatwiej jest wyznaczyć y, ponieważ ma współczynnik 1:
y = 7 - 3x -
Krok 2: Podstawiamy wyrażenie do drugiego równania. Teraz wstawiamy 7 - 3x w miejsce y do drugiego równania 5x - 2y = 1. Pamiętaj o nawiasach!
5x - 2(7 - 3x) = 1 -
Krok 3: Rozwiązujemy równanie z jedną niewiadomą.
5x - 14 + 6x = 1 (Rozmnożyliśmy -2 przez każdy wyraz w nawiasie)
11x - 14 = 1 (Zredukowaliśmy wyrazy podobne)
11x = 1 + 14 (Przenieśliśmy -14 na drugą stronę ze zmianą znaku)
11x = 15
x = 15/11 -
Krok 4: Obliczamy drugą niewiadomą. Podstawiamy obliczone x = 15/11 do wzoru wyznaczonego w Kroku 1: y = 7 - 3x.
y = 7 - 3 * (15/11)
y = 7 - 45/11
y = 77/11 - 45/11
y = 32/11 -
Krok 5: Sprawdzamy rozwiązanie. Wstawiamy x = 15/11 i y = 32/11 do obu początkowych równań.
Równanie 1: 3(15/11) + 32/11 = 45/11 + 32/11 = 77/11 = 7. Zgadza się!
Równanie 2: 5(15/11) - 2(32/11) = 75/11 - 64/11 = 11/11 = 1. Zgadza się!
Rozwiązaniem układu jest para liczb (15/11, 32/11).
Pamiętaj, że rozwiązaniem układu równań jest zawsze para liczb (x, y), która jednocześnie spełnia oba równania. To tak, jakbyś szukał punktu przecięcia dwóch linii na wykresie ten punkt ma konkretne współrzędne x i y.
Typowe problemy i ich rozwiązania: Co robić, gdy coś pójdzie nie tak?
Czasem w trakcie rozwiązywania pojawiają się ułamki, co może być zniechęcające. Moja rada: jeśli równanie z jedną niewiadomą zawiera ułamki, pomnóż obie strony równania przez wspólny mianownik wszystkich ułamków. To pozwoli ci pozbyć się ułamków i kontynuować obliczenia na liczbach całkowitych, co jest znacznie prostsze i zmniejsza ryzyko błędów.
Jak zidentyfikować błędy rachunkowe?
- Sprawdzaj każdy krok: Pośpiech jest wrogiem matematyki. Przejrzyj swoje obliczenia krok po kroku.
- Zwracaj uwagę na znaki: Błędy w znakach przy przenoszeniu wyrazów lub mnożeniu przez liczby ujemne to plaga. Upewnij się, że każdy wyraz ma poprawny znak.
- Nawiasy to twój przyjaciel: Zawsze używaj nawiasów przy podstawianiu całego wyrażenia, a następnie dokładnie je usuwaj, pamiętając o rozdzieleniu mnożenia na wszystkie składniki w nawiasie.
- Weryfikuj podstawienie: Upewnij się, że podstawiasz obliczoną wartość do wzoru z Kroku 1, a nie do początkowego równania, z którego wyznaczyłeś niewiadomą.
Co, jeśli podczas rozwiązywania dojdziesz do wyniku typu 0 = 0? To oznacza, że układ jest nieoznaczony, czyli ma nieskończenie wiele rozwiązań. Oznacza to, że oba równania są w rzeczywistości tym samym równaniem, tylko w innej formie, a ich wykresy pokrywają się.
Z kolei, jeśli otrzymasz sprzeczność, na przykład 3 = 5, to znaczy, że układ jest sprzeczny i nie ma rozwiązań. W takim przypadku linie reprezentowane przez równania są równoległe i nigdy się nie przetną.
Zaawansowane wskazówki: Opanuj metodę do perfekcji
Podsumowując najczęstsze błędy i przekształcając je w konkretne rady:
- Nie spiesz się z przekształceniami: Dokładnie przenoś wyrazy i zmieniaj znaki. To podstawa.
- Nawiasy są obowiązkowe: Zawsze używaj ich przy podstawianiu wyrażenia zawierającego więcej niż jeden składnik.
- Uważaj na rachunki: Podwójnie sprawdzaj mnożenie i dodawanie/odejmowanie, zwłaszcza gdy pojawiają się liczby ujemne.
- Podstawiaj do właściwego miejsca: Obliczoną wartość pierwszej niewiadomej zawsze podstawiaj do wzoru wyznaczonego w pierwszym kroku, aby znaleźć drugą.
Warto również wiedzieć, że metoda przeciwnych współczynników, o której wspomniałem wcześniej, może być bardziej efektywna w sytuacjach, gdy łatwo jest uzyskać przeciwne współczynniki przy jednej z niewiadomych. Na przykład, jeśli masz x + y = 5 i x - y = 1, dodanie stronami obu równań od razu eliminuje y. Wybór metody zależy od konkretnego układu równań.
Aby naprawdę opanować metodę podstawiania, zachęcam Cię do rozwiązywania jak największej liczby przykładów. Szukaj zadań z ułamkami, większymi liczbami, czy też takimi, gdzie trzeba uważać na znaki. Praktyka czyni mistrza!

