Prawdopodobieństwo: kostka i moneta jak liczyć bezbłędnie?

Rozwiązywanie zadań z rachunku prawdopodobieństwa, zwłaszcza tych łączących rzut kostką i monetą, może wydawać się na początku skomplikowane. Ten artykuł to kompleksowy przewodnik, który krok po kroku przeprowadzi Cię przez metodologię analizy takich zdarzeń losowych, pomoże zrozumieć kluczowe wzory i przygotuje do egzaminów, takich jak matura.

Zrozumienie podstaw: dlaczego kostka i moneta to idealny start

Zadania z rzutem kostką i monetą to prawdziwa klasyka w nauczaniu rachunku prawdopodobieństwa, szczególnie w polskiej szkole średniej. Nie bez powodu często pojawiają się na sprawdzianach i są niemal pewnym elementem matury podstawowej z matematyki. Ich fenomen polega na tym, że stanowią doskonały punkt wyjścia do zrozumienia fundamentalnych zasad. Są na tyle proste, że łatwo jest wypisać wszystkie możliwe wyniki, ale jednocześnie na tyle złożone, by móc przećwiczyć kluczowe pojęcia, takie jak przestrzeń zdarzeń elementarnych, zdarzenia sprzyjające czy interpretacja spójników "i" oraz "lub". To właśnie na ich przykładzie najłatwiej jest zbudować solidne fundamenty, które przydadzą się w przyszłości przy bardziej skomplikowanych zagadnieniach.

Krok 1: Określenie przestrzeni zdarzeń czym jest Twoja Omega (Ω)?

Zanim zaczniemy cokolwiek obliczać, musimy zrozumieć, co dokładnie może się wydarzyć w naszym eksperymencie. W rachunku prawdopodobieństwa nazywamy to przestrzenią zdarzeń elementarnych, oznaczaną grecką literą Omega (Ω). Jest to nic innego jak zbiór wszystkich możliwych, wzajemnie wykluczających się wyników danego doświadczenia losowego. W przypadku jednoczesnego rzutu sześcienną kostką do gry i monetą, każdy element Omegi to para, gdzie pierwszy element to wynik rzutu monetą (Orzeł lub Reszka), a drugi to liczba oczek na kostce (od 1 do 6).

Jak poprawnie wypisać wszystkie możliwe wyniki rzutu kostką i monetą?

Aby mieć pewność, że niczego nie pominiemy, warto wypisywać elementy Omegi systematycznie. Możemy to zrobić, grupując wyniki według tego, co wypadło na monecie, a następnie przypisując do tego wszystkie możliwe wyniki z kostki. To prosta, ale skuteczna metoda:

• (O, 1)
• (O, 2)
• (O, 3)
• (O, 4)
• (O, 5)
• (O, 6)
• (R, 1)
• (R, 2)
• (R, 3)
• (R, 4)
• (R, 5)
• (R, 6)

Ile dokładnie wynosi moc Omegi (ilość wszystkich zdarzeń) i dlaczego to kluczowe?

Moc Omegi, oznaczana jako |Ω|, to po prostu liczba wszystkich elementów w przestrzeni zdarzeń elementarnych. W naszym przypadku, gdy mamy 2 możliwe wyniki rzutu monetą (Orzeł lub Reszka) i 6 możliwych wyników rzutu kostką (1, 2, 3, 4, 5, 6), moc Omegi obliczamy, mnożąc te liczby: 2 * 6 = 12. Zatem |Ω| = 12. Prawidłowe określenie mocy Omegi jest absolutnie kluczowe, ponieważ to właśnie ona stanowi mianownik w klasycznym wzorze na prawdopodobieństwo. Każdy błąd na tym etapie skutkuje niepoprawnym wynikiem końcowym, dlatego zawsze warto poświęcić chwilę, aby upewnić się, że |Ω| jest obliczone poprawnie.

Obliczanie prawdopodobieństwa w praktyce: od teorii do rozwiązania

Gdy już mamy solidne podstawy, czyli wiemy, co to jest Omega i jak ją wyznaczyć, możemy przejść do sedna rachunku prawdopodobieństwa obliczania szans na wystąpienie konkretnych zdarzeń. To właśnie tutaj teoria spotyka się z praktyką, a my zaczynamy faktycznie rozwiązywać zadania.

Czym jest zdarzenie sprzyjające? Wyszukiwanie wyników, które pasują do polecenia

Zdarzenie sprzyjające, oznaczane zazwyczaj dużą literą (np. A), to podzbiór Omegi, czyli zbiór tych wszystkich wyników doświadczenia losowego, które spełniają określony warunek z polecenia zadania. Innymi słowy, są to te "szczęśliwe" wyniki, na które czekamy. Kluczem do sukcesu jest precyzyjne odczytanie warunku i dokładne wypisanie wszystkich elementów Omegi, które go spełniają. Często zadania wymagają od nas nie tylko zrozumienia warunku, ale także umiejętności interpretacji spójników "i" oraz "lub", które mają fundamentalne znaczenie dla poprawnego wyznaczenia zdarzeń sprzyjających.

Klasyczna definicja prawdopodobieństwa złoty wzór, który musisz znać

Gdy już znamy moc Omegi (|Ω|) i liczbę zdarzeń sprzyjających (|A|), możemy zastosować klasyczną definicję prawdopodobieństwa. Jest to podstawowe narzędzie, które musisz znać i rozumieć. Wzór jest prosty i intuicyjny:

P(A) = |A| / |Ω|

Gdzie:

• P(A) to prawdopodobieństwo zajścia zdarzenia A.
• |A| to liczba zdarzeń sprzyjających zdarzeniu A.
• |Ω| to moc przestrzeni zdarzeń elementarnych (liczba wszystkich możliwych wyników).

Przykład #1: Jakie jest prawdopodobieństwo wyrzucenia orła i parzystej liczby oczek?

Przyjrzyjmy się pierwszemu, prostemu przykładowi, który pomoże nam zastosować poznane zasady w praktyce. Zadanie brzmi: "Jakie jest prawdopodobieństwo wyrzucenia orła i parzystej liczby oczek?".

Analiza zdarzenia sprzyjającego "A" krok po kroku

W tym zadaniu szukamy wyników, które spełniają dwa warunki jednocześnie, połączone spójnikiem "i": musi wypaść Orzeł ORAZ parzysta liczba oczek. Przejdźmy przez naszą Omegę i wybierzmy te elementy, które spełniają oba kryteria:

• (O, 1) - Nie, bo 1 nie jest parzyste.
• (O, 2) - Tak!
• (O, 3) - Nie, bo 3 nie jest parzyste.
• (O, 4) - Tak!
• (O, 5) - Nie, bo 5 nie jest parzyste.
• (O, 6) - Tak!
• (R, 1) - Nie, bo to Reszka.
• ...i tak dalej dla wszystkich wyników z Reszką.

Zatem zdarzenie A (wyrzucenie orła i parzystej liczby oczek) to zbiór: A = {(O, 2), (O, 4), (O, 6)}. Moc tego zdarzenia wynosi |A| = 3.

Podstawienie do wzoru i obliczenie wyniku

Wiemy, że moc Omegi |Ω| = 12, a moc zdarzenia sprzyjającego |A| = 3. Teraz wystarczy podstawić te wartości do wzoru na prawdopodobieństwo:

P(A) = |A| / |Ω| = 3 / 12 = 1/4

Prawdopodobieństwo wyrzucenia orła i parzystej liczby oczek wynosi 1/4 (lub 25%).

Przykład #2: Oblicz prawdopodobieństwo wyrzucenia reszki lub liczby oczek większej niż 4

Teraz zmierzymy się z nieco bardziej złożonym zadaniem, które wprowadza spójnik "lub". Polecenie brzmi: "Oblicz prawdopodobieństwo wyrzucenia reszki lub liczby oczek większej niż 4".

Uwaga na spójnik "lub" jak wpływa na obliczenia?

Spójnik "lub" oznacza sumę zdarzeń. To znaczy, że interesują nas wszystkie wyniki, które spełniają PIERWSZY warunek, LUB DRUGI warunek, LUB OBA warunki jednocześnie. W teorii prawdopodobieństwa istnieje wzór na prawdopodobieństwo sumy zdarzeń: P(A U B) = P(A) + P(B) - P(A ∩ B). Jednak w przypadku tak małej Omegi, jak dla kostki i monety, często łatwiej jest po prostu intuicyjnie wypisać wszystkie zdarzenia, które spełniają choć jeden z warunków, pamiętając, aby nie liczyć tych samych elementów dwukrotnie. To właśnie poprawna interpretacja spójnika "lub" jest kluczowa dla uniknięcia błędów.

Wyznaczanie zdarzeń sprzyjających dla sumy zbiorów

• Zdefiniujmy zdarzenie A jako "wyrzucenie reszki":
  A = {(R,1), (R,2), (R,3), (R,4), (R,5), (R,6)}.
• Zdefiniujmy zdarzenie B jako "wyrzucenie liczby oczek większej niż 4" (czyli 5 lub 6):
  B = {(O,5), (O,6), (R,5), (R,6)}.
• Zdarzenie A ∩ B (część wspólna, czyli "reszka I liczba oczek większa niż 4") to:
  A ∩ B = {(R,5), (R,6)}.
• Teraz wypiszmy elementy zdarzenia A U B (suma, czyli "reszka LUB liczba oczek większa niż 4"), pamiętając, aby nie powtarzać elementów z części wspólnej:
  A U B = {(R,1), (R,2), (R,3), (R,4), (R,5), (R,6), (O,5), (O,6)}.
  Moc tego zdarzenia wynosi |A U B| = 8.
• Obliczmy prawdopodobieństwo:
  P(A U B) = |A U B| / |Ω| = 8 / 12 = 2/3.

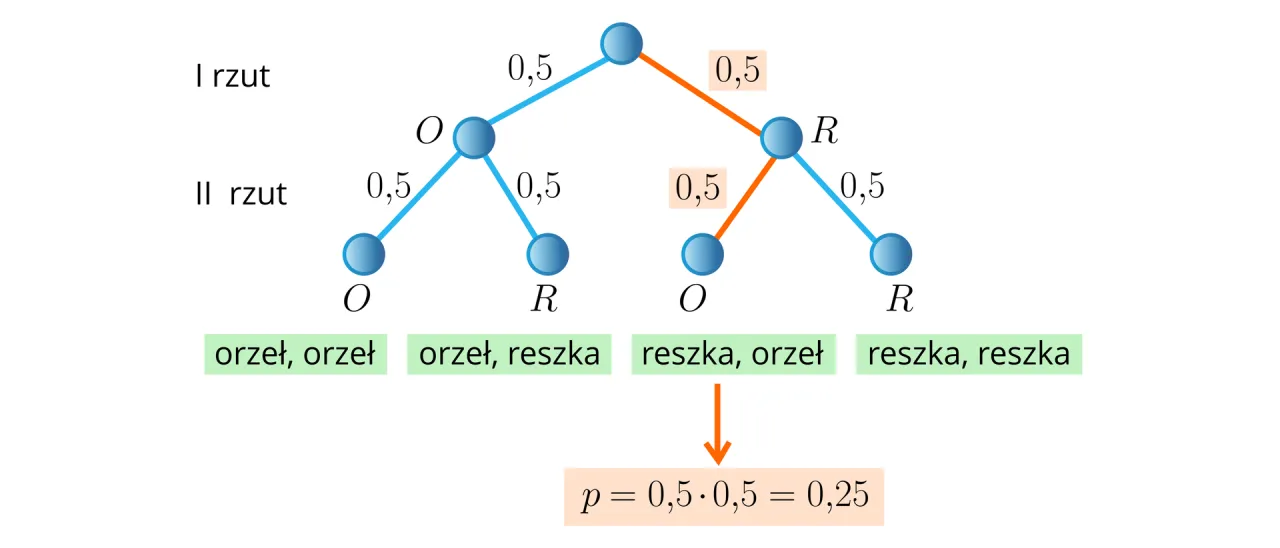
Wizualizacja problemu: metoda drzewka stochastycznego

Czasami, zwłaszcza gdy warunki zadania stają się bardziej złożone, samo wypisywanie elementów Omegi może być mylące. W takich sytuacjach z pomocą przychodzi metoda drzewka stochastycznego potężne narzędzie wizualne, które pozwala uporządkować wszystkie możliwe wyniki i ich prawdopodobieństwa.

Jak narysować drzewko stochastyczne dla rzutu monetą i kostką?

Rysowanie drzewka stochastycznego dla rzutu monetą i kostką jest dość proste i intuicyjne:

1. Rozpocznij od punktu początkowego: To jest nasz początek doświadczenia.
2. Pierwszy etap rzut monetą: Od punktu początkowego narysuj dwie główne gałęzie. Jedna będzie reprezentować wyrzucenie Orła (O), druga Reszki (R). Przy każdej gałęzi możesz zapisać prawdopodobieństwo (1/2 dla Orła, 1/2 dla Reszki).
3. Drugi etap rzut kostką: Od końca każdej z tych dwóch głównych gałęzi (czyli od Orła i od Reszki) poprowadź po sześć kolejnych gałęzi. Każda z nich będzie reprezentować jeden z wyników rzutu kostką (1, 2, 3, 4, 5, 6). Przy każdej z tych gałęzi zapisz prawdopodobieństwo (1/6 dla każdego oczka).
4. Odczytywanie wyników: Na końcu każdej ścieżki (czyli połączenia głównej gałęzi z jedną z sześciu mniejszych) otrzymasz jeden element przestrzeni zdarzeń elementarnych, np. (O, 1), (O, 2), ..., (R, 6).

Odczytywanie prawdopodobieństwa z gałęzi drzewka praktyczne wskazówki

Drzewko stochastyczne nie tylko pomaga wizualizować Omegę, ale także ułatwia obliczanie prawdopodobieństwa zdarzeń. Prawdopodobieństwo konkretnego wyniku (np. (O, 2)) odczytujesz, mnożąc prawdopodobieństwa na gałęziach, które do niego prowadzą (w tym przypadku 1/2 * 1/6 = 1/12). Aby obliczyć prawdopodobieństwo zdarzenia złożonego (np. "orzeł i parzysta liczba oczek"), identyfikujesz wszystkie ścieżki, które spełniają ten warunek, a następnie sumujesz prawdopodobieństwa tych ścieżek. Jest to szczególnie pomocne, gdy czujesz, że "gubisz się w obliczeniach" lub po prostu potrzebujesz wizualnego potwierdzenia swoich wyników.

Najczęstsze pułapki i błędy w zadaniach z prawdopodobieństwa

Nawet doświadczonym osobom zdarzają się pomyłki, a rachunek prawdopodobieństwa, choć wydaje się prosty, ma swoje pułapki. Jako Igor Lis, często widzę, jak studenci i uczniowie wpadają w te same sidła. Oto najczęstsze błędy, na które musisz uważać, oraz wskazówki, jak ich unikać.

Mylenie spójników "i" oraz "lub" jak je poprawnie interpretować?

• "I" oznacza iloczyn zdarzeń (część wspólną). Szukamy wyników, które spełniają oba warunki jednocześnie. Na przykład, "Orzeł i 6 oczek" to tylko (O, 6).
• "LUB" oznacza sumę zdarzeń. Szukamy wyników, które spełniają przynajmniej jeden z warunków (pierwszy, drugi, lub oba). Na przykład, "Orzeł lub 6 oczek" to {(O,1), (O,2), (O,3), (O,4), (O,5), (O,6), (R,6)}. Pamiętaj, aby nie liczyć tych samych wyników dwukrotnie!

Błędne obliczanie mocy Omegi skąd biorą się pomyłki?

Kolejnym częstym błędem jest nieprawidłowe określenie liczby wszystkich możliwych zdarzeń, czyli mocy Omegi (|Ω|). Uczniowie potrafią zapomnieć o wszystkich kombinacjach, np. licząc tylko wyniki dla Orła, a pomijając Reszkę. W przypadku rzutu kostką i monetą, moc Omegi to zawsze 12 (2 możliwości dla monety * 6 możliwości dla kostki). Jeśli masz wątpliwości, wypisz wszystkie elementy Omegi, tak jak pokazałem to wcześniej, lub skorzystaj z drzewka stochastycznego. To proste doświadczenie, ale błąd w mianowniku sprawi, że całe zadanie będzie źle rozwiązane.

Niewłaściwe wypisywanie zdarzeń sprzyjających jak robić to systematycznie?

Pośpiech i brak systematyczności to wrogowie poprawnego wyznaczania zdarzeń sprzyjających. Często zdarza się, że uczniowie pomijają niektóre wyniki lub, co gorsza, wpisują te, które nie spełniają warunku. Aby tego uniknąć, polecam następujące metody:

• Tworzenie list: Wypisuj elementy Omegi i zaznaczaj te, które spełniają warunek.
• Tabelaryczne zestawienia: Dla bardziej złożonych zadań, tabela może pomóc w organizacji wyników.
• Drzewko stochastyczne: Jak już wspominałem, drzewko to świetne narzędzie wizualne, które pozwala na przejrzyste zidentyfikowanie wszystkich zdarzeń.

Nigdy nie polegaj wyłącznie na pamięci, zwłaszcza pod presją czasu. Systematyczność to klucz do sukcesu.

Co dalej po opanowaniu podstaw rzutu kostką i monetą?

Gratulacje! Jeśli czujesz się pewnie w rozwiązywaniu zadań z rzutem kostką i monetą, to znaczy, że masz już solidne podstawy rachunku prawdopodobieństwa. Ale to dopiero początek fascynującej podróży. Ta wiedza to fundament, który otworzy Ci drzwi do bardziej zaawansowanych zagadnień.

Zdarzenia niezależne dlaczego rzut kostką i monetą to ich podręcznikowy przykład?

Rzut kostką i monetą to podręcznikowy przykład zdarzeń niezależnych. Co to oznacza? To proste: wynik rzutu monetą w żaden sposób nie wpływa na wynik rzutu kostką, i odwrotnie. Są to zdarzenia, które dzieją się obok siebie, nie ingerując w swoje rezultaty. Ta niezależność jest kluczową właściwością w prawdopodobieństwie i pozwala na zastosowanie prostego, ale bardzo ważnego wzoru: P(A∩B) = P(A) * P(B). Oznacza to, że prawdopodobieństwo zajścia obu zdarzeń niezależnych jednocześnie jest równe iloczynowi ich indywidualnych prawdopodobieństw. Zrozumienie tego konceptu na przykładzie kostki i monety ułatwi Ci dalsze poznawanie bardziej skomplikowanych zagadnień.

Jak wiedza o kostce i monecie przyda Ci się w bardziej złożonych zadaniach?

Opanowanie podstaw na przykładzie kostki i monety jest absolutnie niezbędne do rozwiązywania bardziej złożonych zadań z rachunku prawdopodobieństwa. Ta wiedza to Twój punkt startowy do:

• Analizowania doświadczeń z większą liczbą rzutów (np. dwoma kostkami, trzema monetami).
• Pracy z innymi obiektami losowymi (np. losowanie kart, kul z urny).
• Zrozumienia prawdopodobieństwa warunkowego (na poziomie rozszerzonym), gdzie wynik jednego zdarzenia wpływa na prawdopodobieństwo drugiego.
• Poznawania schematu Bernoulliego i innych rozkładów prawdopodobieństwa.

Wszystkie te zaawansowane koncepcje opierają się na tych samych fundamentalnych zasadach, które właśnie opanowałeś. Im lepiej rozumiesz Omegę, zdarzenia sprzyjające i podstawowy wzór, tym łatwiej będzie Ci przyswoić bardziej skomplikowane zagadnienia.