NWD: Rozkład na czynniki pierwsze zrozumiesz raz na zawsze!

Największy Wspólny Dzielnik (NWD) to jedno z tych pojęć matematycznych, które na początku mogą wydawać się abstrakcyjne, ale w rzeczywistości są niezwykle praktyczne i fundamentalne dla dalszej nauki. To nic innego jak największa liczba, która dzieli bez reszty dwie lub więcej liczb całkowitych, a jego zrozumienie otwiera drzwi do wielu innych zagadnień, takich jak skracanie ułamków czy rozwiązywanie zadań tekstowych. W tym artykule, jako Igor Lis, poprowadzę Cię krok po kroku przez metodę rozkładu na czynniki pierwsze klasyczny i bardzo obrazowy sposób obliczania NWD, idealny dla uczniów i wszystkich, którzy chcą odświeżyć swoją wiedzę.

Zanim zaczniesz: Kluczowe pojęcia matematyczne

Zanim zagłębimy się w samą metodę obliczania NWD, musimy upewnić się, że rozumiemy podstawowe pojęcia. Bez nich, jak w każdym rzemiośle, trudno będzie nam sprawnie posługiwać się narzędziami. Przygotowałem dla Ciebie krótkie, ale treściwe przypomnienie.

Czym jest dzielnik i dlaczego ma znaczenie?

Dzielnik liczby to każda liczba naturalna, przez którą możemy podzielić daną liczbę bez reszty. Proste, prawda? Zrozumienie dzielników jest absolutnie fundamentalne dla NWD, ponieważ szukamy przecież największego wspólnego dzielnika. Na przykład, dzielniki liczby 12 to (1, 2, 3, 4, 6, 12). Dzielniki liczby 18 to (1, 2, 3, 6, 9, 18). Widzisz, które z nich są wspólne? To właśnie od tego zaczyna się cała idea NWD.

Liczby pierwsze fundament całej metody rozkładu

W metodzie rozkładu na czynniki pierwsze kluczową rolę odgrywają liczby pierwsze. Liczba pierwsza to taka liczba naturalna, która ma dokładnie dwa dzielniki: jedynkę i samą siebie (np. 2, 3, 5, 7, 11, 13...). Z kolei liczba złożona to każda liczba naturalna większa od 1, która nie jest liczbą pierwszą, czyli ma więcej niż dwa dzielniki (np. 4, 6, 8, 9, 10...). Dlaczego to takie ważne? Ponieważ w rozkładzie na czynniki pierwsze używamy wyłącznie liczb pierwszych. To one są "cegiełkami", z których budujemy wszystkie inne liczby.

Na czym polega rozkład na czynniki pierwsze? Szybka powtórka na przykładach

Rozkład liczby na czynniki pierwsze to nic innego jak przedstawienie jej w postaci iloczynu liczb pierwszych. Istnieją dwie popularne metody: "drzewko" i pionowy słupek. Obie są skuteczne, a wybór zależy od Twoich preferencji. Weźmy przykład liczby 36. Rozkładając ją, możemy zapisać: 36 = 2 * 18 = 2 * 2 * 9 = 2 * 2 * 3 * 3. Jak widzisz, na końcu mamy tylko liczby pierwsze (2 i 3). To jest właśnie to, o co nam chodzi!

NWD metodą rozkładu na czynniki pierwsze: Instrukcja krok po kroku

Teraz, gdy mamy już solidne podstawy, możemy przejść do sedna, czyli do instrukcji obliczania NWD metodą rozkładu na czynniki pierwsze. To proste i logiczne podejście, które, jestem przekonany, szybko opanujesz.

Krok 1: Rozłóż każdą z liczb na czynniki pierwsze (metoda "drzewka")

Pierwszym i najważniejszym krokiem jest rozłożenie każdej z danych liczb na czynniki pierwsze. Pamiętaj, aby używać tylko liczb pierwszych (2, 3, 5, 7 itd.) do dzielenia. Możesz to zrobić za pomocą wspomnianej wcześniej metody "drzewka" lub pionowego słupka wybierz tę, która jest dla Ciebie bardziej intuicyjna. Ważne, aby rozkład był kompletny, czyli na końcu zostały Ci same liczby pierwsze.

Krok 2: Wytrop wspólne czynniki to klucz do rozwiązania!

Gdy już masz rozkłady wszystkich liczb, czas na detektywistyczną pracę. Twoim zadaniem jest zidentyfikowanie wspólnych czynników pierwszych. Co to znaczy? Szukaj tych liczb pierwszych, które występują w rozkładzie każdej z analizowanych liczb. Jeśli jakaś liczba pierwsza występuje w rozkładach wielokrotnie, bierzesz ją pod uwagę tyle razy, ile razy występuje wspólnie we wszystkich rozkładach. Na przykład, jeśli w jednym rozkładzie masz trzy dwójki, a w drugim dwie dwójki, to wspólnie występują dwie dwójki.

Krok 3: Wymnóż znalezione czynniki, aby otrzymać NWD

Ostatni krok to już czysta formalność. Wszystkie wspólne czynniki pierwsze, które udało Ci się wytropić w Kroku 2, musisz teraz pomnożyć przez siebie. Wynik tego mnożenia to właśnie szukany Największy Wspólny Dzielnik (NWD). To naprawdę takie proste!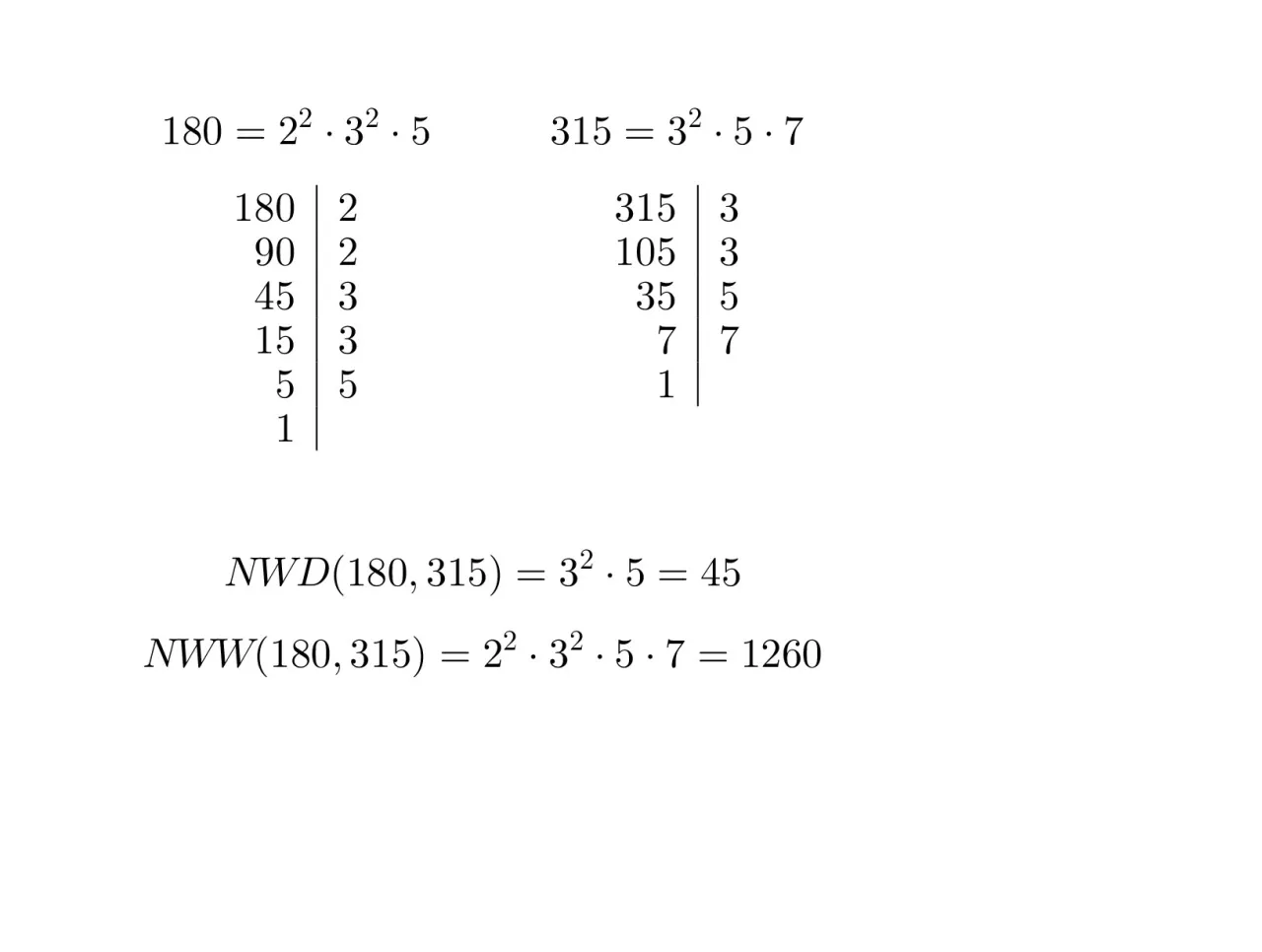

NWD w praktyce: Przykłady, które rozwieją wątpliwości

Teoria to jedno, ale prawdziwe zrozumienie przychodzi z praktyką. Dlatego przygotowałem dla Ciebie kilka przykładów, które krok po kroku pokażą, jak zastosować metodę rozkładu na czynniki pierwsze. Zobaczysz, że to nic trudnego.

Przykład 1: Obliczanie NWD dla małych liczb (np. 12 i 18)

Obliczmy NWD dla liczb 12 i 18.

1. Rozkład liczby 12: 12 = 2 * 2 * 3
2. Rozkład liczby 18: 18 = 2 * 3 * 3
3. Wspólne czynniki: W obu rozkładach występuje jedna dwójka i jedna trójka.
4. NWD(12, 18) = 2 * 3 = 6

Przykład 2: Jak poradzić sobie z nieco większymi liczbami? (np. 48 i 72)

Teraz weźmy nieco większe liczby: 48 i 72.

1. Rozkład liczby 48: 48 = 2 * 2 * 2 * 2 * 3
2. Rozkład liczby 72: 72 = 2 * 2 * 2 * 3 * 3
3. Wspólne czynniki: Widzimy, że wspólnie występują trzy dwójki i jedna trójka.
4. NWD(48, 72) = 2 * 2 * 2 * 3 = 24

Przykład 3: Co zrobić, gdy liczb jest więcej niż dwie? (NWD dla 16, 24, 40)

Co, jeśli mamy do czynienia z trzema liczbami? Zasada jest dokładnie taka sama! Wspólne czynniki muszą występować we *wszystkich* rozkładach.

1. Rozkład liczby 16: 16 = 2 * 2 * 2 * 2
2. Rozkład liczby 24: 24 = 2 * 2 * 2 * 3
3. Rozkład liczby 40: 40 = 2 * 2 * 2 * 5
4. Wspólne czynniki: W każdym z trzech rozkładów występują trzy dwójki.
5. NWD(16, 24, 40) = 2 * 2 * 2 = 8

Najczęstsze pułapki i błędy w obliczaniu NWD

Nawet najprostsze metody mają swoje pułapki. Jako doświadczony nauczyciel, widziałem wiele razy, jak uczniowie wpadają w te same błędy. Poznaj je, a będziesz mógł ich uniknąć!

Błąd #1: Mylenie czynników pierwszych ze wszystkimi dzielnikami

To bardzo częsty błąd. Pamiętaj, że dzielniki liczby to wszystkie liczby, przez które dana liczba dzieli się bez reszty (np. dzielniki 12 to 1, 2, 3, 4, 6, 12). Natomiast czynniki pierwsze to tylko te liczby pierwsze, które tworzą iloczyn danej liczby (np. czynniki pierwsze 12 to 2, 2, 3). Do obliczania NWD metodą rozkładu na czynniki pierwsze bierzemy pod uwagę wyłącznie czynniki pierwsze, a nie wszystkie dzielniki!

Błąd #2: Niedokładny rozkład na czynniki zgubiony element układanki

Innym błędem jest niekompletny rozkład liczby. Czasami uczniowie zatrzymują się w połowie, na przykład pisząc 12 = 2 * 6. Sześć nie jest liczbą pierwszą! Pamiętaj, że rozkład musi składać się wyłącznie z liczb pierwszych. Zawsze zadawaj sobie pytanie: "Czy ta liczba jest pierwsza? Jeśli nie, to muszę ją rozłożyć dalej!".

Błąd #3: Co w sytuacji, gdy liczby nie mają wspólnych czynników pierwszych? (Liczby względnie pierwsze)

Nie zawsze znajdziesz wspólne czynniki pierwsze inne niż 1. Kiedy tak się dzieje, mówimy, że liczby są względnie pierwsze. Ich NWD wynosi wtedy 1. Na przykład, NWD(7, 15) = 1. Dlaczego? Ponieważ 7 = 7 (jest liczbą pierwszą), a 15 = 3 * 5. Nie ma żadnych wspólnych czynników pierwszych, więc ich NWD to 1. To ważna zasada, o której łatwo zapomnieć!

Po co nam NWD? Praktyczne zastosowania w zadaniach i życiu

Matematyka to nie tylko teoria. NWD, choć na pierwszy rzut oka może wydawać się abstrakcyjne, ma mnóstwo praktycznych zastosowań. Pokażę Ci, gdzie możesz je spotkać zarówno w szkolnych zadaniach, jak i w codziennym życiu.

Jak NWD pomaga skracać ułamki do najprostszej postaci?

Jednym z najczęstszych zastosowań NWD jest skracanie ułamków zwykłych. Aby ułamek był w postaci nieskracalnej, musimy podzielić jego licznik i mianownik przez ich Największy Wspólny Dzielnik. Weźmy ułamek 12/18. Jak już obliczyliśmy, NWD(12, 18) = 6. Dzieląc licznik (12) i mianownik (18) przez 6, otrzymujemy 2/3. I voilà! Ułamek 2/3 jest nieskracalny, bo NWD(2, 3) = 1.

Rozwiązywanie zadań tekstowych klasyka szkolna (np. dzielenie na grupy)

NWD jest niezastąpione w rozwiązywaniu wielu zadań tekstowych, zwłaszcza tych, które dotyczą dzielenia przedmiotów na największe, identyczne grupy. Klasyczny przykład: "Mamy 24 jabłka i 36 gruszek. Ile największych, identycznych koszyków możemy przygotować, aby w każdym było tyle samo jabłek i gruszek?". Aby to rozwiązać, potrzebujesz NWD(24, 36). Obliczając je, dowiesz się, ile takich koszyków możesz przygotować i ile owoców każdego rodzaju znajdzie się w jednym koszyku. NWD(24, 36) = 12, więc możesz przygotować 12 koszyków, a w każdym będą 2 jabłka (24/12) i 3 gruszki (36/12).

NWD w codziennych problemach: cięcie materiałów bez odpadów

Wyobraź sobie, że masz dwie wstążki o długościach 60 cm i 90 cm i chcesz pociąć je na równe, jak najdłuższe kawałki, tak aby nie było żadnych odpadów. Jaką długość powinny mieć te kawałki? Odpowiedzią jest NWD(60, 90). Obliczając je, dowiesz się, że NWD(60, 90) = 30. Oznacza to, że możesz pociąć obie wstążki na kawałki o długości 30 cm, bez marnowania materiału. Podobnie NWD przydaje się przy układaniu płytek pomaga znaleźć największe kwadratowe płytki, którymi można wyłożyć prostokątną powierzchnię bez konieczności ich docinania.

Metoda rozkładu to nie wszystko: Kiedy warto znać Algorytm Euklidesa?

Chociaż metoda rozkładu na czynniki pierwsze jest świetna do nauki podstaw i pracy z mniejszymi liczbami, w matematyce i informatyce istnieje inne, znacznie wydajniejsze narzędzie do obliczania NWD, zwłaszcza dla bardzo dużych liczb. Mowa o Algorytmie Euklidesa.

Czym jest Algorytm Euklidesa i dlaczego jest tak szybki?

Algorytm Euklidesa to starożytna, ale niezwykle sprytna metoda obliczania NWD, która nie wymaga rozkładania liczb na czynniki pierwsze. Działa ona na zasadzie kolejnych odejmowań lub dzieleń z resztą. Jej główną zaletą jest to, że jest znacznie szybsza i bardziej efektywna, gdy mamy do czynienia z dużymi liczbami, których rozkład na czynniki pierwsze byłby bardzo czasochłonny, a czasem wręcz niemożliwy do wykonania ręcznie. To właśnie ten algorytm jest podstawą wielu obliczeń w kryptografii i informatyce.

Przeczytaj również: Notacja wykładnicza: Zapisz małe liczby bezbłędnie! Poradnik

Porównanie metod: Kiedy rozkład na czynniki jest lepszy, a kiedy warto użyć algorytmu?

Obie metody mają swoje miejsce i zastosowanie. Wybór zależy od kontekstu i wielkości liczb.

Metoda	Zalety / Kiedy stosować
Metoda rozkładu na czynniki pierwsze	Bardzo obrazowa i intuicyjna, idealna do nauki podstaw NWD. Doskonała dla małych i średnich liczb. Pomaga zrozumieć strukturę liczb i pojęcie czynników pierwszych.
Algorytm Euklidesa	Niezwykle szybki i efektywny, szczególnie dla bardzo dużych liczb. Preferowany w informatyce i zaawansowanych obliczeniach. Nie wymaga znajomości czynników pierwszych, co jest zaletą przy trudnych do faktoryzacji liczbach.