Dzielenie licznika przez mianownik uniwersalna metoda zamiany ułamków zwykłych na dziesiętne
- Zamiana ułamka zwykłego na dziesiętny polega na podzieleniu licznika przez mianownik.
- Metoda dzielenia pisemnego jest uniwersalna; gdy licznik jest mniejszy, zaczynamy od "0," i dopisujemy zera.
- Wynikiem może być rozwinięcie dziesiętne skończone (reszta 0) lub nieskończone okresowe (powtarzające się reszty).
- W przypadku liczb mieszanych, część całkowitą przepisujemy, a dzielimy tylko część ułamkową.
- Opanowanie tej metody jest kluczowym elementem programu nauczania matematyki w szkołach podstawowych.
Dzielenie pisemne dlaczego to uniwersalny klucz do ułamków?
Zastanawiałeś się kiedyś, dlaczego kreska ułamkowa jest tak często nazywana znakiem dzielenia? To dlatego, że w swojej istocie ułamek zwykły to nic innego jak niewykonane dzielenie. Licznik to dzielna, a mianownik to dzielnik. Kiedy chcemy zamienić ułamek zwykły na dziesiętny, po prostu wykonujemy to dzielenie. Metoda dzielenia pisemnego jest w tym kontekście absolutnie fundamentalna, ponieważ działa zawsze bez wyjątków. Nie musisz szukać wspólnego mianownika, rozszerzać ułamka do potęgi dziesiątki (co często jest niemożliwe), ani stosować żadnych innych sztuczek.Dzielenie pisemne to uniwersalny algorytm, który pozwala przekształcić każdy ułamek zwykły w jego odpowiednik dziesiętny, niezależnie od tego, czy będzie to rozwinięcie skończone, czy nieskończone okresowe. Opanowanie tej techniki to nie tylko umiejętność rozwiązywania konkretnego typu zadań, ale przede wszystkim głębsze zrozumienie struktury liczb i ich wzajemnych relacji. To fundament, na którym buduje się dalszą wiedzę matematyczną, dlatego warto poświęcić czas na jego solidne przyswojenie.
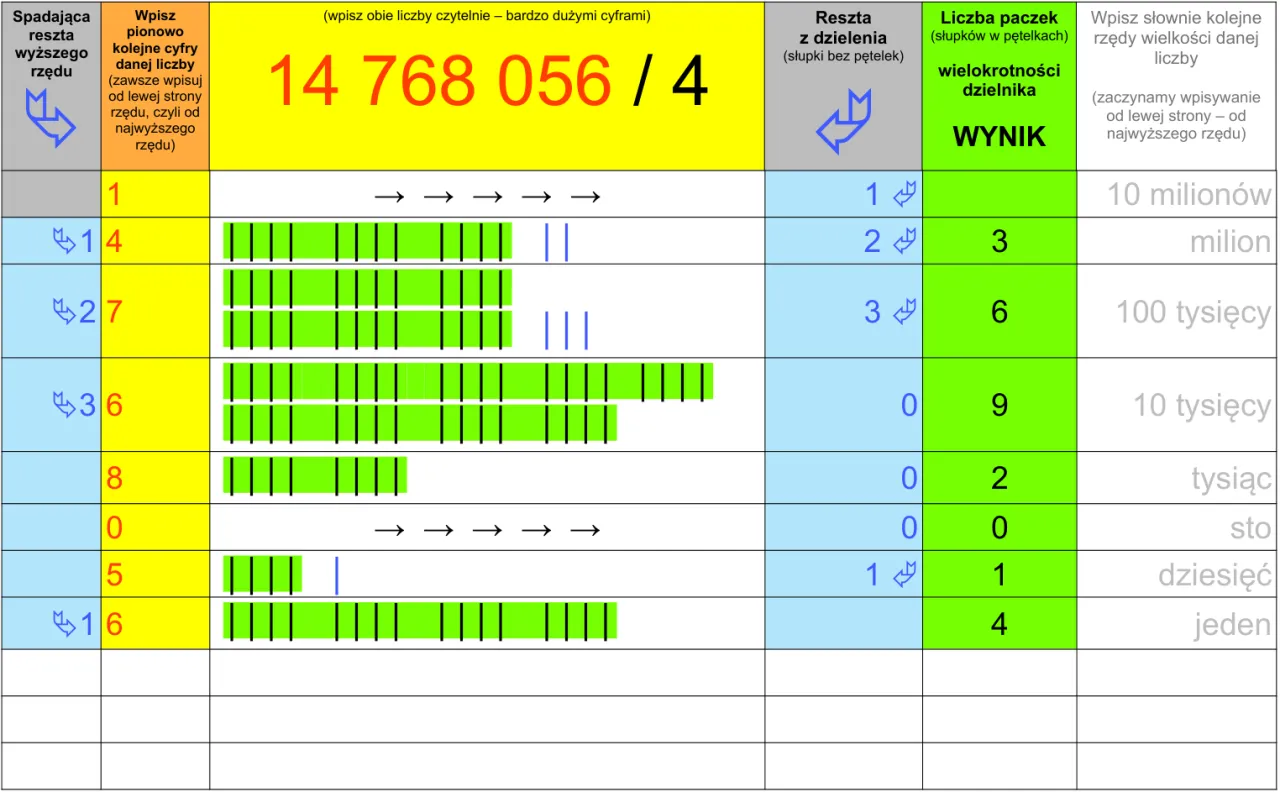
Przygotowanie do dzielenia prosty schemat działania
Zanim przejdziemy do konkretnych przykładów, ustalmy prosty schemat, który pozwoli Ci prawidłowo rozpocząć każde dzielenie pisemne. Pamiętaj, że kluczem jest precyzja i cierpliwość.
- Ustawienie dzielenia: Zapisz ułamek zwykły w formie dzielenia pisemnego. Licznik ułamka staje się dzielną (liczba pod kreską), a mianownik dzielnikiem (liczba przed kreską). Na przykład dla ułamka 3/4, trójka będzie pod kreską, a czwórka przed nią.
- Co, gdy licznik jest mniejszy od mianownika? To bardzo częsta sytuacja. Jeśli dzielna (licznik) jest mniejsza od dzielnika (mianownika), w wyniku od razu wpisujemy "0," (zero i przecinek). Następnie do dzielnej dopisujemy zero i kontynuujemy dzielenie. To kluczowy moment, który pozwala nam przejść do części dziesiętnej liczby.
- Kontynuacja dzielenia: Dzielimy tak, jakbyśmy dzielili liczby całkowite, dopisując kolejne zera do reszty, aż do momentu, gdy reszta wyniesie zero (rozwinięcie skończone) lub zacznie się powtarzać (rozwinięcie okresowe). Pamiętaj, aby cyfry w wyniku zapisywać nad odpowiednimi cyframi dzielnej.
Zamiana ułamka na liczbę dziesiętną: instrukcja i przykłady
Teraz przejdźmy do praktyki. Pokażę Ci, jak krok po kroku zamieniać ułamki na ich dziesiętne odpowiedniki, zaczynając od tych, które mają rozwinięcie skończone.
Jak zamienić ułamek 3/4 na postać dziesiętną?
Weźmy ułamek 3/4. Musimy podzielić 3 przez 4. Ponieważ 3 jest mniejsze od 4, w wyniku od razu zapisujemy 0,. Następnie dopisujemy zero do trójki, uzyskując 30. Teraz dzielimy 30 przez 4. Otrzymujemy 7, ponieważ 4 * 7 = 28. Od 30 odejmujemy 28, zostaje nam reszta 2. Do tej reszty dopisujemy kolejne zero, tworząc 20. Dzielimy 20 przez 4, co daje nam 5. Tym razem reszta wynosi 0, co oznacza, że dzielenie się zakończyło. Wynik to 0,75. Jest to przykład rozwinięcia dziesiętnego skończonego, ponieważ proces dzielenia zakończył się bez reszty.
0,75 ----- 4 | 3,00 - 0 --- 3 0 - 2 8 ----- 2 0 - 2 0 ----- 0
Zamiana ułamka 5/8 na liczbę dziesiętną
Kolejny przykład to 5/8. Dzielimy 5 przez 8. Ponieważ 5 < 8, w wyniku piszemy 0, i dopisujemy zero do 5, otrzymując 50. Dzielimy 50 przez 8. Najbliżej jest 6 (8 * 6 = 48). Od 50 odejmujemy 48, zostaje reszta 2. Do reszty 2 dopisujemy zero, mamy 20. Dzielimy 20 przez 8. Najbliżej jest 2 (8 * 2 = 16). Od 20 odejmujemy 16, zostaje reszta 4. Dopisujemy kolejne zero, mamy 40. Dzielimy 40 przez 8, co daje nam 5 (8 * 5 = 40). Reszta wynosi 0. Dzielenie zakończone. Wynik to 0,625. To również rozwinięcie dziesiętne skończone.
0,625 ------ 8 | 5,000 - 0 ---- 5 0 - 4 8 ----- 2 0 - 1 6 ----- 4 0 - 4 0 ----- 0

Ułamki okresowe co, gdy dzielenie się nie kończy?
Nie każde dzielenie kończy się zerową resztą. Czasami, podczas dzielenia, reszty zaczynają się powtarzać w określonej sekwencji. Kiedy tak się dzieje, oznacza to, że mamy do czynienia z ułamkiem o rozwinięciu dziesiętnym nieskończonym okresowym. Powtarzająca się sekwencja cyfr w wyniku to tak zwany "okres", który zapisujemy w nawiasie.
Jak rozpoznać ułamek o rozwinięciu nieskończonym na przykładzie 2/3?
Spróbujmy podzielić 2 przez 3. Ponieważ 2 < 3, w wyniku piszemy 0, i dopisujemy zero do 2, uzyskując 20. Dzielimy 20 przez 3. Otrzymujemy 6 (3 * 6 = 18). Od 20 odejmujemy 18, zostaje reszta 2. Dopisujemy zero do reszty 2, mamy znowu 20. Dzielimy 20 przez 3, znowu otrzymujemy 6 i resztę 2. Jak widzisz, reszta 2 będzie powtarzać się w nieskończoność, a w wyniku zawsze będziemy otrzymywać cyfrę 6. Oznacza to, że 6 jest okresem. Ułamek 2/3 zapisujemy jako 0,(6).
0,666... ------- 3 | 2,000 - 0 ---- 2 0 - 1 8 ----- 2 0 - 1 8 ----- 2 (reszta się powtarza)
Zapis 0,(6) oznacza, że cyfra 6 powtarza się w nieskończoność: 0,666666...
Przykład praktyczny: Zamiana ułamka 5/6 na postać dziesiętną z okresem
Teraz nieco bardziej złożony przykład: 5/6. Dzielimy 5 przez 6. Ponieważ 5 < 6, w wyniku piszemy 0, i dopisujemy zero do 5, uzyskując 50. Dzielimy 50 przez 6. Otrzymujemy 8 (6 * 8 = 48). Od 50 odejmujemy 48, zostaje reszta 2. Dopisujemy zero do reszty 2, mamy 20. Dzielimy 20 przez 6. Otrzymujemy 3 (6 * 3 = 18). Od 20 odejmujemy 18, zostaje reszta 2. I znowu! Reszta 2 się powtarza, co oznacza, że od tego momentu cyfra 3 będzie się powtarzać w wyniku. Okresem jest więc cyfra 3. Wynik to 0,8(3).
0,833... ------- 6 | 5,000 - 0 ---- 5 0 - 4 8 ----- 2 0 - 1 8 ----- 2 0 - 1 8 ----- 2 (reszta się powtarza)
W tym przypadku okres (3) nie zaczyna się od razu po przecinku. Pierwsza cyfra po przecinku (8) nie jest częścią okresu. Zapis 0,8(3) oznacza 0,833333...
Liczby mieszane jak je zamienić na ułamek dziesiętny?
Jeśli masz do czynienia z liczbą mieszaną, na przykład 4 1/5, proces jest jeszcze prostszy. Część całkowitą zostawiamy w spokoju i zajmujemy się tylko częścią ułamkową. Po zamianie części ułamkowej na dziesiętną, po prostu dodajemy ją do części całkowitej.
Przeczytaj również: Jak narysować parabolę? Wykres funkcji kwadratowej od A do Z
Jak zamienić 4 1/5 na ułamek dziesiętny metodą dzielenia?
- Zostawiamy część całkowitą (4) w spokoju. Będzie ona naszą liczbą przed przecinkiem.
- Dzielimy tylko licznik przez mianownik z części ułamkowej, czyli 1 przez 5.
0,2 ---- 5 | 1,0 - 0 --- 1 0 - 1 0 ----- 0
Uzyskujemy 0,2. - Łączymy wyniki poprzez proste dodawanie do całości: 4 + 0,2 = 4,2.
Najczęstsze pułapki i błędy jak ich unikać?
Podczas dzielenia pisemnego, zwłaszcza na początku, łatwo o drobne pomyłki. Oto najczęstsze pułapki i wskazówki, jak ich unikać:
- Złe umiejscowienie przecinka w wyniku: Pamiętaj, że przecinek w wyniku pojawia się natychmiast po tym, jak po raz pierwszy dopiszesz zero do licznika (lub reszty), gdy jest on mniejszy od mianownika. Jeśli dzielisz 3 przez 4, po dopisaniu zera do 3 (uzyskując 30), w wyniku masz już "0,". Dalsze zera dopisujesz już po przecinku.
- Gubienie zer podczas odejmowania w słupku: Dzielenie pisemne wymaga precyzji. Upewnij się, że dokładnie odejmujesz i prawidłowo dopisujesz zera do reszty. Każde pominięte lub źle dopisane zero może całkowicie zmienić wynik. Warto pisać cyfry starannie, jedna pod drugą, aby uniknąć pomyłek.
- Niepoprawne rozpoznanie i zapisanie okresu: Okres to sekwencja cyfr, która faktycznie się powtarza. Upewnij się, że reszta, która prowadzi do tej sekwencji, pojawiła się już wcześniej. Czasami jedna lub dwie cyfry mogą być poza okresem (jak w przykładzie 0,8(3)). Zawsze używaj nawiasów do oznaczenia tylko tych cyfr, które faktycznie tworzą powtarzający się cykl.

