Kolejność działań z nawiasami i potęgami: Opanuj i unikaj błędów!

Wprowadzenie do zasad kolejności wykonywania działań matematycznych jest kluczowe dla każdego, kto chce poprawnie rozwiązywać zadania. Ten artykuł to praktyczny przewodnik, który w prosty sposób wyjaśni reguły dotyczące nawiasów i potęg, pomagając uniknąć typowych błędów i zbudować solidne podstawy matematyczne.

Z mojego doświadczenia jako eksperta wynika, że znajomość kolejności wykonywania działań jest absolutną podstawą w matematyce. Bez niej, nawet najprostsze zadania mogą prowadzić do błędnych wyników. To jak budowanie domu bez fundamentów prędzej czy później konstrukcja się zawali. Zrozumienie tej hierarchii pozwala na spójne i logiczne podejście do rozwiązywania problemów, co jest niezbędne na każdym etapie edukacji, od szkoły podstawowej po studia wyższe.

Błędy wynikające z pomylenia kolejności działań mają bardzo praktyczne i często frustrujące konsekwencje. Wyobraź sobie, że rozwiązujesz skomplikowane zadanie, wkładasz w nie wiele wysiłku, a ostateczny wynik jest zły tylko dlatego, że pomyliłeś kolejność mnożenia z dodawaniem. To nie tylko prowadzi do nieprawidłowych odpowiedzi, ale także może zniechęcać do dalszej nauki matematyki i budować fałszywe przekonanie o własnych brakach. Wiele problemów, które widzę u uczniów, wynika właśnie z tego podstawowego niedopatrzenia.

Nawiasy Twój pierwszy przystanek

Zawsze, ale to zawsze, działania w nawiasach mają absolutny priorytet. Niezależnie od tego, co znajduje się w środku, musisz rozwiązać to jako pierwsze. Nawiasy pełnią funkcję "izolatora" oddzielają pewne fragmenty wyrażenia, wskazując, że należy je potraktować jako jedną, spójną operację, zanim przejdziemy do reszty zadania. To kluczowa zasada, której nie wolno ignorować.

W matematyce spotykamy się z różnymi rodzajami nawiasów: okrągłymi `()`, kwadratowymi `[]` i klamrowymi `{}`. Ważne jest, aby zrozumieć, że wszystkie one pełnią tę samą funkcję wskazują na priorytet działania. Różne kształty nawiasów są używane głównie dla czytelności, zwłaszcza gdy mamy do czynienia z nawiasami zagnieżdżonymi. Dzięki temu łatwiej jest śledzić, które nawiasy do siebie pasują.

Jeśli w wyrażeniu pojawiają się nawiasy zagnieżdżone, czyli nawiasy w nawiasach, obowiązuje zasada "od środka na zewnątrz". Oznacza to, że zawsze zaczynamy od działań w najbardziej wewnętrznych nawiasach. Dopiero po ich rozwiązaniu przechodzimy do nawiasów zewnętrznych. Spójrzmy na prosty przykład: `2 * (3 + (4 - 1))`. Tutaj najpierw obliczamy `4 - 1 = 3`, potem `3 + 3 = 6`, a na końcu `2 * 6 = 12`.

Oto kilka przykładów, które ilustrują, jak poprawnie postępować z nawiasami:

1. Prosty przykład: `5 + (8 - 3) * 2`
   1. Najpierw rozwiązujemy działanie w nawiasie: `8 - 3 = 5`.
   2. Wyrażenie staje się: `5 + 5 * 2`.
   3. Następnie wykonujemy mnożenie (priorytet przed dodawaniem): `5 * 2 = 10`.
   4. Na koniec dodajemy: `5 + 10 = 15`.
2. Przykład z nawiasami zagnieżdżonymi: `10 - [2 * (6 - 4) + 1]`
   1. Zaczynamy od najbardziej wewnętrznego nawiasu okrągłego: `6 - 4 = 2`.
   2. Wyrażenie staje się: `10 - [2 * 2 + 1]`.
   3. Teraz rozwiązujemy nawias kwadratowy, zaczynając od mnożenia: `2 * 2 = 4`.
   4. Następnie dodajemy w nawiasie kwadratowym: `4 + 1 = 5`.
   5. Wyrażenie staje się: `10 - 5`.
   6. Na koniec odejmujemy: `10 - 5 = 5`.

Potęgowanie i pierwiastkowanie drugi w kolejce

Po uporaniu się z nawiasami, kolejnym krokiem w hierarchii działań jest potęgowanie i pierwiastkowanie. Te dwie operacje mają ten sam priorytet i wykonuje się je przed mnożeniem i dzieleniem. To często pomijany, ale niezwykle ważny element, który ma ogromny wpływ na ostateczny wynik.

Potęgowanie to skrócony zapis wielokrotnego mnożenia tej samej liczby przez siebie. Na przykład, `2^3` to `2 * 2 * 2`. Dlaczego ma ono wyższy priorytet niż zwykłe mnożenie? Ponieważ jest to bardziej "złożona" forma mnożenia, a matematyka dąży do upraszczania i grupowania operacji. Wykonując potęgowanie jako pierwsze, utrzymujemy spójność i logiczność całego systemu.

Zarówno potęgowanie, jak i pierwiastkowanie (które jest operacją odwrotną do potęgowania) mają równy priorytet. Oznacza to, że jeśli w wyrażeniu pojawią się obok siebie, wykonujemy je w kolejności od lewej do prawej. Nie ma tu zasady, że jedno jest "ważniejsze" od drugiego. Po prostu idziemy zgodnie z naturalnym kierunkiem czytania.

Jedną z najczęstszych pułapek, na którą natykam się u moich uczniów, jest potęgowanie liczb ujemnych. Tutaj kluczowe jest rozróżnienie między `(-3)²` a `-3²`. W pierwszym przypadku, `(-3)²`, nawiasy wskazują, że cała liczba -3 jest podnoszona do potęgi. Oznacza to `(-3) * (-3)`, co daje wynik 9. Minus razy minus daje plus. Natomiast w drugim przypadku, `-3²`, potęgowana jest tylko liczba 3, a znak minus jest traktowany jako oddzielna operacja negacji, wykonywana po potęgowaniu. Zatem `3²` to 9, a następnie do wyniku dodajemy minus, co daje -9. Ta subtelna różnica jest często źródłem błędów, dlatego zawsze zwracam na nią szczególną uwagę.

Mnożenie i dzielenie równe sobie, od lewej do prawej

Po nawiasach i potęgach przychodzi czas na mnożenie i dzielenie. Te dwie operacje mają równy priorytet. To bardzo ważne, ponieważ wielu uczniów błędnie zakłada, że mnożenie zawsze wyprzedza dzielenie. Pamiętaj, że jeśli w wyrażeniu występują zarówno mnożenie, jak i dzielenie, wykonujemy je w kolejności, w jakiej pojawiają się od lewej do prawej.

To mit, że mnożenie jest "ważniejsze" od dzielenia. Takie myślenie często prowadzi do błędów. Matematyka jest precyzyjna, a zasada "od lewej do prawej" dla działań o tym samym priorytecie jest niezmienna. Jeśli masz `12 / 2 * 3`, poprawne rozwiązanie to najpierw `12 / 2 = 6`, a następnie `6 * 3 = 18`. Gdybyśmy najpierw wykonali mnożenie, otrzymalibyśmy `12 / (2 * 3) = 12 / 6 = 2`, co jest wynikiem niepoprawnym.

Spójrzmy na przykłady, gdzie błędne zastosowanie kolejności może wprowadzić w błąd:

1. Przykład 1: `20 / 5 * 2`
   1. Błędne podejście: Jeśli najpierw pomnożymy `5 * 2 = 10`, a potem podzielimy `20 / 10`, otrzymamy 2.
   2. Poprawne podejście: Zgodnie z zasadą "od lewej do prawej", najpierw dzielimy: `20 / 5 = 4`.
   3. Następnie mnożymy: `4 * 2 = 8`. Poprawny wynik to 8.
2. Przykład 2: `3 * 4 / 6`
   1. Błędne podejście: Jeśli najpierw podzielimy `4 / 6` (co daje ułamek), a potem pomnożymy, skomplikujemy sobie obliczenia i możemy popełnić błąd.
   2. Poprawne podejście: Idziemy od lewej do prawej. Najpierw mnożymy: `3 * 4 = 12`.
   3. Następnie dzielimy: `12 / 6 = 2`. Poprawny wynik to 2.

Kiedy mamy do czynienia z działaniami pod kreską ułamkową, warto pamiętać o ważnej zasadzie: licznik i mianownik ułamka należy traktować jako wyrażenia w domyślnych nawiasach. Oznacza to, że najpierw musisz wykonać wszystkie działania w liczniku, potem wszystkie działania w mianowniku, a dopiero na końcu wykonać dzielenie. Na przykład, w ułamku `(6 + 2) / (4 - 2)`, najpierw obliczamy licznik `6 + 2 = 8`, potem mianownik `4 - 2 = 2`, a na końcu dzielimy `8 / 2 = 4`.

Dodawanie i odejmowanie na końcu, ale ważne

Wreszcie, na samym końcu hierarchii działań, mamy dodawanie i odejmowanie. Podobnie jak mnożenie i dzielenie, te dwie operacje mają równy priorytet. Oznacza to, że jeśli w wyrażeniu pojawiają się obok siebie, wykonujemy je w kolejności, w jakiej występują od lewej do prawej. To ostatni, ale równie ważny krok w procesie rozwiązywania zadań.

Aby zademonstrować zasadę "od lewej do prawej" dla dodawania i odejmowania, spójrzmy na prosty przykład: `10 - 3 + 5`. Poprawne rozwiązanie to najpierw `10 - 3 = 7`, a następnie `7 + 5 = 12`. Gdybyśmy najpierw dodali `3 + 5 = 8`, a potem odjęli `10 - 8`, otrzymalibyśmy 2, co jest błędem. Pamiętaj, że konsekwencja w stosowaniu tej zasady jest kluczowa.

Jednym z klasycznych błędów, który często widzę, jest niewłaściwe opuszczanie nawiasów, zwłaszcza gdy przed nimi stoi znak minus. Zasada jest prosta: jeśli przed nawiasem jest znak minus, to przy jego opuszczaniu zmieniamy znaki wszystkich wyrazów wewnątrz nawiasu na przeciwne. Na przykład, `5 - (3 + 2)` to nie to samo co `5 - 3 + 2`. Poprawnie powinniśmy to obliczyć jako `5 - 3 - 2 = 0`. Jeśli mielibyśmy `5 - (3 - 2)`, to po opuszczeniu nawiasu otrzymujemy `5 - 3 + 2 = 4`. To drobiazg, ale ma ogromne znaczenie dla poprawności wyniku.

Złożone przykłady w praktyce

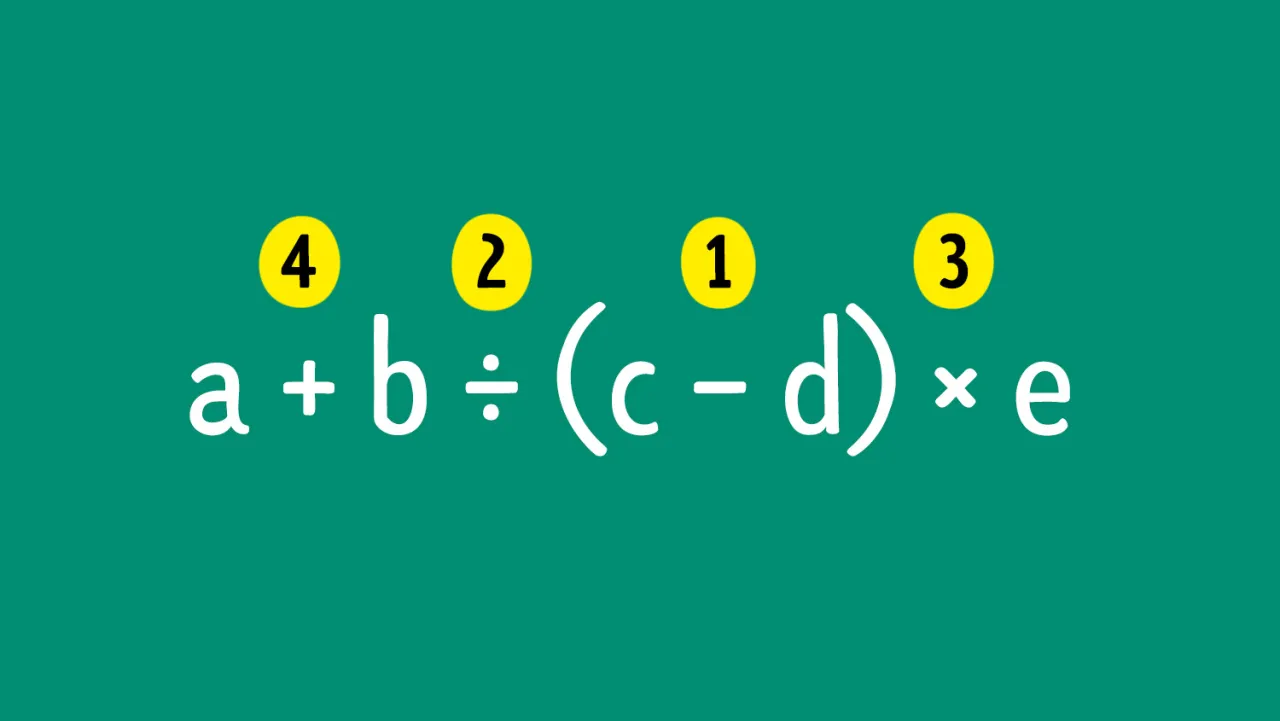
Teraz, kiedy omówiliśmy wszystkie zasady, nadszedł czas, aby zobaczyć, jak działają one w praktyce. Poniższe przykłady pokażą, jak krok po kroku rozwiązywać bardziej złożone wyrażenia matematyczne, stosując wszystkie omówione reguły hierarchii działań.

1. Zadanie: `15 - [ (4 + 2)² / 3 - 5 ] * 2`
2. Krok 1: Rozwiąż nawias wewnętrzny okrągły: `(4 + 2) = 6`.

   Wyrażenie staje się: `15 - [ 6² / 3 - 5 ] * 2`

3. Krok 2: Wykonaj potęgowanie w nawiasie kwadratowym: `6² = 36`.

   Wyrażenie staje się: `15 - [ 36 / 3 - 5 ] * 2`

4. Krok 3: Wykonaj dzielenie w nawiasie kwadratowym: `36 / 3 = 12`.

   Wyrażenie staje się: `15 - [ 12 - 5 ] * 2`

5. Krok 4: Wykonaj odejmowanie w nawiasie kwadratowym: `12 - 5 = 7`.

   Wyrażenie staje się: `15 - 7 * 2`

6. Krok 5: Wykonaj mnożenie (ma priorytet przed odejmowaniem): `7 * 2 = 14`.

   Wyrażenie staje się: `15 - 14`

7. Krok 6: Wykonaj odejmowanie: `15 - 14 = 1`.

   Ostateczny wynik to 1.

Typowe zadanie szkolne często wygląda tak: "Oblicz wartość wyrażenia: `(10 + 2 * 3) / 4 - 2^2`". Potencjalne pułapki to: najpierw dodanie 10 do 2, zamiast pomnożenia, oraz błędne obliczenie potęgi.

1. Zadanie: `(10 + 2 * 3) / 4 - 2^2`
2. Krok 1: W nawiasie najpierw mnożenie: `2 * 3 = 6`.

   Wyrażenie w nawiasie staje się: `(10 + 6) = 16`.

   Całe wyrażenie: `16 / 4 - 2^2`

3. Krok 2: Potęgowanie: `2^2 = 4`.

   Całe wyrażenie: `16 / 4 - 4`

4. Krok 3: Dzielenie: `16 / 4 = 4`.

   Całe wyrażenie: `4 - 4`

5. Krok 4: Odejmowanie: `4 - 4 = 0`.

   Ostateczny wynik to 0.

Przedstawię teraz działanie, które na pierwszy rzut oka wydaje się proste, ale zawiera podstęp, wymagający precyzyjnego zastosowania zasady "od lewej do prawej" oraz rozróżnienia między potęgowaniem liczb ujemnych: `10 - 2 * 3^2 + (-2)^3`.

1. Zadanie: `10 - 2 * 3^2 + (-2)^3`
2. Krok 1: Potęgowanie `3^2`: `3 * 3 = 9`.

   Wyrażenie staje się: `10 - 2 * 9 + (-2)^3`

3. Krok 2: Potęgowanie `(-2)^3`: `(-2) * (-2) * (-2) = 4 * (-2) = -8`.

   Wyrażenie staje się: `10 - 2 * 9 + (-8)`

4. Krok 3: Mnożenie: `2 * 9 = 18`.

   Wyrażenie staje się: `10 - 18 + (-8)`

5. Krok 4: Od lewej do prawej: odejmowanie: `10 - 18 = -8`.

   Wyrażenie staje się: `-8 + (-8)`

6. Krok 5: Dodawanie: `-8 + (-8) = -16`.

   Ostateczny wynik to -16.

Jak skutecznie ćwiczyć i unikać błędów?

Samo zrozumienie zasad to połowa sukcesu. Druga połowa to konsekwentne ćwiczenie i rozwijanie nawyku poprawnego rozwiązywania zadań. Chcę podzielić się z Wami kilkoma sprawdzonymi metodami, które pomogą Wam unikać typowych błędów i budować pewność siebie w matematyce.

Stwórz sobie krótką listę kontrolną, którą będziesz weryfikować przy rozwiązywaniu każdego działania. To proste narzędzie znacząco zmniejszy ryzyko pomyłek:

1. Nawiasy: Czy wykonałem wszystkie działania w nawiasach, zaczynając od najbardziej wewnętrznych?
2. Potęgi i pierwiastki: Czy poprawnie obliczyłem wszystkie potęgi i pierwiastki? Czy zwróciłem uwagę na znaki przy potęgowaniu liczb ujemnych?
3. Mnożenie i dzielenie: Czy wykonałem mnożenie i dzielenie w kolejności od lewej do prawej?
4. Dodawanie i odejmowanie: Czy wykonałem dodawanie i odejmowanie w kolejności od lewej do prawej?
5. Znaki: Czy poprawnie zastosowałem zasady zmiany znaków przy opuszczaniu nawiasów ze znakiem minus?

Pamiętajcie, że błędy są częścią procesu nauki, ale warto znać te najpopularniejsze, aby świadomie ich unikać:

• Mylenie priorytetów mnożenia/dzielenia: Wielu uczniów wciąż uważa, że mnożenie jest zawsze ważniejsze. Pamiętaj: równy priorytet, od lewej do prawej! Zawsze to powtarzam, bo to klucz do sukcesu.
• Błędne potęgowanie liczb ujemnych: Jak już wspomniałem, różnica między `(-X)^Y` a `-X^Y` jest fundamentalna. Zawsze sprawdzaj, czy minus jest w nawiasie, czy poza nim.
• Niewłaściwe opuszczanie nawiasów: Znak minus przed nawiasem zmienia znaki w środku. To pułapka, na którą łatwo wpaść, ale świadomość tej zasady pozwala jej uniknąć.
• Błędy przy działaniach pod kreską ułamkową: Traktuj licznik i mianownik jako osobne wyrażenia w nawiasach. To pomoże Ci uniknąć bałaganu i zachować porządek w obliczeniach.

Aby ułatwić sobie zapamiętanie kolejności działań, możesz zastosować różne techniki:

• Akronimy: W języku angielskim popularny jest akronim PEMDAS (Parentheses, Exponents, Multiplication, Division, Addition, Subtraction) lub BODMAS (Brackets, Orders, Division, Multiplication, Addition, Subtraction). W Polsce możemy stworzyć swój własny, np. Nawiasy, Potęgi, Mnożenie/Dzielenie, Dodawanie/Odejmowanie.
• Rymowanki: Stwórz krótką, chwytliwą rymowankę, która pomoże Ci zapamiętać kolejność. Na przykład: "Najpierw nawiasy, potem potęgi, by wynik był zgodny z matematyki reguły. Mnożenie z dzieleniem idą w parze, dodawanie z odejmowaniem na końcu, to jest to, co zawsze się marze."
• Wizualizacje: Narysuj piramidę lub drabinę, gdzie na szczycie są nawiasy, a na dole dodawanie i odejmowanie. Codzienne patrzenie na taki schemat pomoże utrwalić kolejność.