Jak obliczyć skalę mapy i odległość w terenie? Twój poradnik!

Co to jest skala i dlaczego nie jest tylko szkolnym wymysłem?

Zacznijmy od podstaw: skala mapy to nic innego jak stosunek odległości zmierzonej na mapie do odpowiadającej jej odległości w rzeczywistości. Brzmi prosto, prawda? I takie jest! W praktyce oznacza to, ile razy dany obszar został pomniejszony, aby zmieścić się na papierze. Często spotykam się z przekonaniem, że skala to tylko nudny element lekcji geografii. Nic bardziej mylnego! Jako ekspert mogę z całą stanowczością powiedzieć, że umiejętność posługiwania się skalą to kluczowa kompetencja, która wykracza daleko poza szkolną ławkę. Wyobraź sobie, że planujesz górską wycieczkę, harcerski rajd czy po prostu chcesz sprawdzić, ile kilometrów musisz pokonać, by dotrzeć do celu. Bez zrozumienia skali mapy, takie zadania stają się czystą zgadywanką. To właśnie skala pozwala mi precyzyjnie ocenić czas marszu, zaplanować zapasy wody czy po prostu nie zgubić się w terenie. Jest to narzędzie, które daje realną kontrolę nad podróżą i otoczeniem.

Trzy twarze skali: liczbowa, mianowana i podziałka liniowa którą wybrać?

Kiedy mówimy o skali, musimy pamiętać, że ma ona kilka form zapisu. Każda z nich ma swoje zalety i jest przydatna w nieco innych sytuacjach. Poznajmy je bliżej.

Skala liczbowa jest najbardziej uniwersalna i najczęściej spotykana. Zapisuje się ją w formie ułamka lub proporcji, na przykład 1:100 000. Oznacza to, że 1 jednostka długości na mapie (np. 1 centymetr) odpowiada 100 000 takim samym jednostkom w terenie (czyli 100 000 centymetrom). Jest to czysty stosunek, który wymaga od nas przeliczenia jednostek, aby uzyskać zrozumiałą odległość w metrach czy kilometrach. Jest to podstawa do wszelkich obliczeń.

Skala mianowana to nic innego jak skala liczbowa przetłumaczona na bardziej intuicyjny język. Zamiast 1:100 000, zobaczymy zapis typu "1 cm = 1 km". Jak to powstaje? Po prostu zamieniamy 100 000 cm na kilometry (100 000 cm = 1000 m = 1 km). Ta forma jest niezwykle wygodna, ponieważ od razu widzimy, ile rzeczywistego dystansu odpowiada jednemu centymetrowi na mapie. Osobiście bardzo ją lubię za szybkość interpretacji, zwłaszcza w terenie, gdy liczy się każda sekunda.

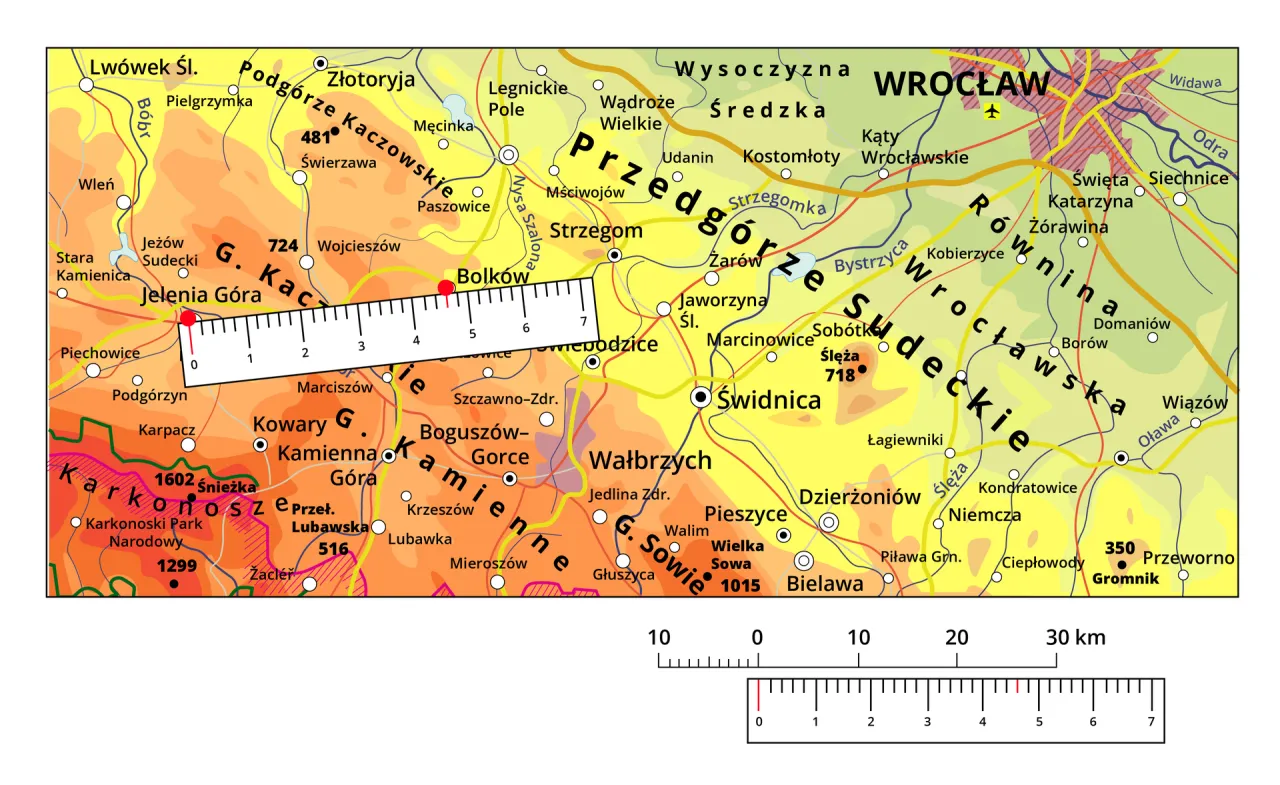
Podziałka liniowa to graficzne przedstawienie skali, które znajdziesz zazwyczaj na dole mapy. Wygląda jak linijka z zaznaczonymi odcinkami odpowiadającymi konkretnym odległościom w terenie (np. 0, 1 km, 2 km). Jej największą zaletą jest to, że pozwala na błyskawiczne mierzenie odległości za pomocą linijki, nitki czy nawet krawędzi kartki, bez konieczności wykonywania jakichkolwiek obliczeń. Jest niezastąpiona, gdy nie masz pod ręką kalkulatora lub po prostu chcesz szybko oszacować dystans.

Duża czy mała skala? Proste wyjaśnienie, które rozwieje Twoje wątpliwości

Terminy "duża skala" i "mała skala" często wprowadzają zamieszanie. Wbrew intuicji, duża skala oznacza duże szczegóły i mały obszar, natomiast mała skala to małe szczegóły i duży obszar. Jak to zapamiętać? Pomyśl o mianowniku skali liczbowej. Im mniejsza liczba w mianowniku, tym "większa" jest skala, ponieważ pomniejszenie jest mniejsze, a co za tym idzie, mapa przedstawia mniejszy obszar, ale za to z ogromną dokładnością. Przykładowo, mapa w skali 1:10 000 to mapa o dużej skali zobaczysz na niej pojedyncze budynki, ścieżki, a nawet ławki. Jest idealna do szczegółowego planowania wędrówek. Z kolei mapa w skali 1:1 000 000 to mapa o małej skali obejmuje ogromny obszar, np. całą Polskę, ale z bardzo małą szczegółowością, pokazując jedynie główne drogi i większe miasta. Ja zawsze powtarzam, że to trochę jak z powiększeniem: im większe powiększenie (czyli mniejszy mianownik), tym więcej detali widzimy.

Klucz do sukcesu: niezbędne wzory i przeliczanie jednostek

Teraz, gdy już wiemy, czym jest skala i jakie ma formy, przejdźmy do konkretów czyli do wzorów. Wbrew pozorom, nie ma tu skomplikowanej matematyki. Wystarczy jeden podstawowy wzór, który można łatwo przekształcać, aby obliczyć to, czego akurat potrzebujemy.

Jeden wzór, trzy możliwości jak elastycznie obliczać skalę, odległość w terenie i na mapie

Podstawowy wzór, z którego wychodzimy, to definicja skali: skala = odległość na mapie / odległość w rzeczywistości. Jednak w praktyce wygodniej jest korzystać z jego przekształconych form, w zależności od tego, co chcemy obliczyć:

1. Obliczanie odległości rzeczywistej (d_rz)

   Wzór: d_rz = d_m * S

   Gdzie: d_rz to odległość rzeczywista (w terenie), d_m to odległość na mapie, a S to mianownik skali (np. dla skali 1:50 000, S wynosi 50 000). Ten wzór jest niezastąpiony, gdy masz mapę, zmierzysz na niej odległość i chcesz wiedzieć, ile to jest naprawdę w terenie. To najczęściej używany przeze mnie wariant.

2. Obliczanie skali mapy (S)

   Wzór: S = d_rz / d_m

   Ten wzór pozwala mi ustalić skalę mapy, jeśli znam rzeczywistą odległość między dwoma punktami (np. z drogowskazu) i zmierzę tę samą odległość na mapie. Pamiętaj, że obie odległości muszą być wyrażone w tej samej jednostce, zanim wykonasz dzielenie. Wynik będzie mianownikiem skali liczbowej (np. 50 000, co da skalę 1:50 000).

3. Obliczanie odległości na mapie (d_m)

   Wzór: d_m = d_rz / S

   Ten wzór jest przydatny, gdy wiesz, jaką odległość chcesz pokonać w terenie i masz mapę o znanej skali. Pozwala mi obliczyć, ile centymetrów zajmie ta trasa na mapie. To doskonałe narzędzie do planowania, np. by sprawdzić, czy cała trasa zmieści się na jednym arkuszu papieru.

Centymetry, metry, kilometry jak płynnie przeliczać jednostki i unikać chaosu

Jeśli miałbym wskazać jeden najczęstszy błąd, jaki widzę przy obliczeniach skali, to jest to błędne przeliczanie jednostek. To absolutnie kluczowy element! Aby wszystkie wzory działały poprawnie, musimy sprowadzić wszystkie wartości do wspólnej jednostki. Najczęściej w obliczeniach skali używamy centymetrów, ponieważ skala liczbowa (np. 1:50 000) domyślnie odnosi się do tej samej jednostki po obu stronach (1 cm na mapie = 50 000 cm w terenie). Jeżeli nie ujednolicisz jednostek, wynik będzie całkowicie błędny. To tak, jakbyś próbował dodać jabłka do gruszek po prostu się nie da!

Twoja ściągawka: gotowe przeliczniki, które warto mieć pod ręką

Aby ułatwić Ci życie i uniknąć pomyłek, przygotowałem listę najważniejszych przeliczników:

• 1 metr (m) = 100 centymetrów (cm)
• 1 kilometr (km) = 1000 metrów (m)
• 1 kilometr (km) = 100 000 centymetrów (cm) (bo 1 km = 1000 m * 100 cm/m = 100 000 cm)

Obliczanie odległości w terenie: praktyczne przykłady krok po kroku

Przejdźmy teraz do praktyki. Nic tak nie utrwala wiedzy, jak rozwiązanie konkretnego zadania. Pokażę Ci, jak krok po kroku wykorzystać poznane wzory.

Zadanie 1: Masz odległość na mapie i skalę jak znaleźć dystans w rzeczywistości?

Zadanie: Mapa ma skalę 1:50 000, odległość na mapie między dwoma punktami to 4 cm. Oblicz odległość w rzeczywistości.

1. Zapisz dane:

   • Skala (S) = 50 000 (mianownik skali)
   • Odległość na mapie (d_m) = 4 cm

2. Wybierz odpowiedni wzór:

   Chcemy obliczyć odległość rzeczywistą, więc użyjemy wzoru: d_rz = d_m * S.

3. Podstaw dane do wzoru i wykonaj obliczenia:

   d_rz = 4 cm * 50 000 = 200 000 cm

4. Przelicz wynik na bardziej praktyczne jednostki (metry i kilometry):

   • 200 000 cm / 100 cm/m = 2000 metrów (m)
   • 2000 m / 1000 m/km = 2 kilometry (km)

   Zatem odległość w rzeczywistości wynosi 2 km. Proste, prawda?

Przykład z życia wzięty: planowanie wycieczki z mapą turystyczną 1: 50 000

Wyobraź sobie, że planujesz weekendową wycieczkę w góry. Masz mapę turystyczną w skali 1:50 000. Chcesz przejść z punktu A do punktu B, a na mapie odległość między nimi wynosi 4 cm. Dzięki właśnie wykonanym obliczeniom wiesz, że to 2 kilometry. To daje mi konkretną informację, ile czasu zajmie mi ten odcinek trasy (przyjmując średnią prędkość marszu). To jest właśnie ta praktyczna wartość, o której mówiłem umiejętność czytania mapy staje się Twoją supermocą w terenie, czy to podczas górskich wędrówek, czy harcerskich podchodów.

Co zrobić, gdy trasa jest kręta? Mierzenie odległości na mapie za pomocą nitki

Nie zawsze trasa na mapie jest prostą linią. Często szlaki wiją się przez lasy, wzdłuż rzek czy wokół wzniesień. Jak wtedy zmierzyć odległość? Moja ulubiona metoda to użycie nitki lub sznurka. Przykładam nitkę do początku trasy i dokładnie, centymetr po centymetrze, układam ją wzdłuż krętego szlaku. Kiedy dotrę do końca trasy, zaznaczam punkt na nitce, a następnie prostuję ją i mierzę jej długość zwykłą linijką. Otrzymaną długość w centymetrach mogę potem przeliczyć, korzystając ze skali liczbowej (jak w Zadaniu 1), albo co jest jeszcze szybsze przyłożyć nitkę bezpośrednio do podziałki liniowej na mapie i odczytać dystans. To prosta, ale niezwykle skuteczna technika.

Jak obliczyć skalę mapy, gdy znasz realny dystans?

Czasem zdarza się, że to skala jest niewiadomą. Może masz starą mapę bez wyraźnego oznaczenia skali, albo chcesz stworzyć własną mapę. Wtedy przydaje się umiejętność obliczenia skali.

Zadanie 2: Znasz odległość między miastami jak ustalić skalę mapy samochodowej?

Zadanie: Wiesz, że odległość w terenie między dwoma miastami wynosi 5 km. Na mapie ta sama odległość to 10 cm. Oblicz skalę mapy.

1. Zapisz dane:

   • Odległość rzeczywista (d_rz) = 5 km
   • Odległość na mapie (d_m) = 10 cm

2. Ujednolicz jednostki:

   To jest ten kluczowy moment! Musimy sprowadzić kilometry na centymetry:

   • 5 km = 5 * 1000 m = 5000 m
   • 5000 m = 5000 * 100 cm = 500 000 cm

3. Wybierz odpowiedni wzór:

   Chcemy obliczyć skalę, więc użyjemy wzoru: S = d_rz / d_m.

4. Podstaw dane do wzoru i wykonaj obliczenia:

   S = 500 000 cm / 10 cm = 50 000

5. Zapisz skalę:

   Otrzymany wynik to mianownik skali. Zatem skala mapy wynosi 1:50 000.

Pamiętaj o sprowadzeniu do wspólnej jednostki najważniejszy krok w obliczeniach

Jak widzisz w Zadaniu 2, sprowadzenie wszystkich wartości do tej samej jednostki jest absolutnie fundamentalne. Bez tego kroku, wynik byłby całkowicie błędny. Zawsze, ale to zawsze, upewnij się, że zarówno odległość na mapie, jak i odległość rzeczywista są wyrażone w centymetrach (lub innej wspólnej jednostce), zanim przystąpisz do dzielenia. To prosta zasada, która pozwoli Ci uniknąć większości pomyłek.

Ile centymetrów na mapie? Obliczanie odległości na arkuszu

Ostatni wariant obliczeń dotyczy sytuacji, gdy znasz odległość w terenie i skalę mapy, a chcesz dowiedzieć się, ile miejsca zajmie ta odległość na mapie.

Zadanie 3: Planujesz trasę 3 km ile miejsca zajmie na mapie w skali 1: 100 000?

Zadanie: Planujesz trasę o długości 3 km. Chcesz sprawdzić, ile miejsca zajmie ona na mapie w skali 1:100 000. Oblicz odległość na mapie.

1. Zapisz dane:

   • Odległość rzeczywista (d_rz) = 3 km
   • Skala (S) = 100 000 (mianownik skali)

2. Ujednolicz jednostki:

   Ponownie, musimy przeliczyć kilometry na centymetry:

   • 3 km = 3 * 1000 m = 3000 m
   • 3000 m = 3000 * 100 cm = 300 000 cm

3. Wybierz odpowiedni wzór:

   Chcemy obliczyć odległość na mapie, więc użyjemy wzoru: d_m = d_rz / S.

4. Podstaw dane do wzoru i wykonaj obliczenia:

   d_m = 300 000 cm / 100 000 = 3 cm

5. Zapisz wynik:

   Odległość 3 km zajmie na mapie 3 cm.

Praktyczne zastosowanie: sprawdzanie, czy cała trasa zmieści się na jednym wydruku

Ta umiejętność jest niezwykle przydatna, gdy pracuję z mapami cyfrowymi lub planuję wydruk. Dzięki niej mogę szybko ocenić, czy cała moja planowana trasa, na przykład 30-kilometrowy szlak rowerowy, zmieści się na jednym arkuszu papieru A4, jeśli wydrukuję mapę w konkretnej skali. Jeśli okaże się, że trasa zajmuje 30 cm, a moja kartka ma tylko 21 cm szerokości, to wiem, że muszę albo zmienić skalę, albo wydrukować mapę w kilku częściach. To pozwala mi efektywnie zarządzać przestrzenią i uniknąć frustracji związanej z niekompletnymi wydrukami.

Najczęstsze pułapki i błędy: jak ich unikać i liczyć bezbłędnie?

Nawet doświadczonym zdarzają się pomyłki, zwłaszcza gdy liczymy w pośpiechu. Zebrałem dla Ciebie najczęstsze błędy, abyś mógł ich świadomie unikać.

Błąd nr 1: Gdzie postawić przecinek? Pomyłki w przeliczaniu jednostek

Jak już wspomniałem, to prawdziwa plaga. Zapominanie o przeliczaniu jednostek lub robienie tego błędnie to najczęstsza przyczyna nieprawidłowych wyników. Widziałem to setki razy! Pamiętaj: 1 km to 100 000 cm. Nie 1000, nie 10 000, ale sto tysięcy. Zawsze, zanim zaczniesz podstawiać dane do wzoru, sprowadź wszystkie odległości do tej samej jednostki, najlepiej centymetrów. Możesz sobie wyobrazić, że każdy kilometr to pięć zer po jedynce (100 000), a każdy metr to dwa zera (100). To prosta wizualizacja, która mi pomaga.

Błąd nr 2: Odwrócone działanie kiedy mnożyć, a kiedy dzielić przez skalę?

Kolejnym częstym problemem jest mylenie, kiedy należy pomnożyć, a kiedy podzielić przez mianownik skali. To jest prosta logika: odległość rzeczywista jest ZAWSZE większa niż odległość na mapie (chyba że mapa jest w skali 1:1, ale to rzadkość). Jeśli obliczasz odległość rzeczywistą, a wynik wychodzi mniejszy niż na mapie, to wiesz, że coś poszło nie tak prawdopodobnie podzieliłeś zamiast pomnożyć. I odwrotnie: jeśli obliczasz odległość na mapie, a wynik jest większy niż odległość rzeczywista, to również masz błąd. Zawsze zadaj sobie to pytanie: "Czy ten wynik ma sens w kontekście rzeczywistości?".

Błąd nr 3: Ignorowanie podziałki liniowej, czyli najszybszej metody w terenie

Wielu ludzi zapomina o podziałce liniowej, skupiając się tylko na skali liczbowej i wzorach. To duży błąd! Podziałka liniowa to najszybsza i najbardziej intuicyjna metoda pomiaru odległości, zwłaszcza gdy jesteś w terenie i nie masz czasu ani ochoty na skomplikowane obliczenia. Wystarczy przyłożyć linijkę, krawędź kartki, a nawet palce i odczytać dystans. Ja sam często z niej korzystam, gdy potrzebuję szybkiego oszacowania. Nie lekceważ jej potęgi!

Podsumowanie: Twoja nowa supermoc w czytaniu map

Gratulacje! Przeszedłeś przez cały proces i teraz masz solidne podstawy do swobodnego posługiwania się skalą mapy. To naprawdę cenna umiejętność, która otwiera nowe możliwości.

Krótkie przypomnienie kluczowych zasad utrwal swoją wiedzę

• Skala to stosunek: Pamiętaj, że skala mapy to po prostu stosunek odległości na mapie do odległości w terenie.
• Trzy rodzaje skali: Skala liczbowa (1:X), mianowana (1 cm = Y km) i podziałka liniowa każda ma swoje zastosowanie.
• Ujednolicaj jednostki: Zawsze, ale to zawsze, przeliczaj wszystkie odległości na tę samą jednostkę (najczęściej centymetry) przed wykonaniem obliczeń. To klucz do poprawności!
• Logika działania: Odległość rzeczywista jest większa niż na mapie. Pamiętaj o tym, decydując, czy mnożyć, czy dzielić przez mianownik skali.

Przeczytaj również: Jak narysować parabolę? Wykres funkcji kwadratowej od A do Z

Od teorii do praktyki jak wykorzystać te umiejętności na co dzień?

Niech ta wiedza nie zostanie tylko w teorii! Wykorzystaj ją w praktyce. Planuj swoje wycieczki piesze i rowerowe z nową precyzją, oceniaj odległości na mapach turystycznych, a nawet używaj jej w grach terenowych czy podczas harcerskich wypraw. Zrozumienie skali mapy to nie tylko umiejętność matematyczna; to narzędzie, które daje Ci pewność i niezależność w eksplorowaniu świata. Teraz, gdy masz tę wiedzę, możesz śmiało powiedzieć, że mapy nie mają już przed Tobą żadnych tajemnic!