W tym artykule znajdziesz kompleksowy przewodnik po obliczaniu przekątnych sześcianu i prostopadłościanu. Poznaj gotowe wzory, zrozum ich pochodzenie dzięki twierdzeniu Pitagorasa, a także naucz się rozwiązywać praktyczne zadania i unikać najczęstszych błędów.
Opanuj obliczanie przekątnych sześcianu (a√3) i prostopadłościanu (√(a²+b²+c²)) z naszym przewodnikiem
- Poznasz konkretne wzory na przekątną sześcianu i prostopadłościanu.
- Zrozumiesz, skąd biorą się te wzory, dzięki szczegółowemu wyprowadzeniu z twierdzenia Pitagorasa.
- Nauczysz się odróżniać przekątną bryły od przekątnej ściany, co pozwoli uniknąć błędów.
- Rozwiążesz praktyczne zadania, zarówno te bezpośrednie, jak i te wymagające obliczeń odwrotnych.
- Dowiesz się, na jakie pułapki uważać, aby zawsze uzyskiwać poprawne wyniki.
Co to jest przekątna i jak odróżnić ją od przekątnej ściany?
Zacznijmy od podstaw, bo to właśnie tutaj często pojawiają się nieporozumienia. Przekątna bryły, czyli na przykład sześcianu czy prostopadłościanu, to odcinek, który łączy dwa wierzchołki bryły, ale co ważne nie należą one do tej samej ściany. Wyobraź sobie, że jeden wierzchołek jest w dolnym przednim rogu, a drugi w górnym tylnym rogu. To właśnie jest przekątna bryły.
Z kolei przekątna ściany to odcinek łączący przeciwległe wierzchołki, ale na tej samej, płaskiej ścianie. Dla sześcianu będzie to przekątna kwadratu, a dla prostopadłościanu przekątna prostokąta. Mylenie tych dwóch pojęć to jeden z najczęstszych błędów, który prowadzi do całkowicie błędnych wyników. Zrozumienie tej różnicy jest kluczowe dla poprawnych obliczeń, dlatego zawsze zwracam na to szczególną uwagę.
Jak obliczyć przekątną sześcianu? Wzór i przykłady
Sześcian to bryła, której wszystkie krawędzie mają taką samą długość. To sprawia, że obliczenia są stosunkowo proste. Jeśli masz do czynienia z sześcianem, wystarczy, że znasz długość jednej jego krawędzi. Gotowy wzór na przekątną sześcianu jest następujący:
d = a√3
Gdzie:
- d to długość przekątnej sześcianu (przekątnej bryły).
- a to długość krawędzi sześcianu.
Skąd bierze się ten wzór? Wyprowadzenie krok po kroku z twierdzeniem Pitagorasa
Wzór na przekątną sześcianu nie wziął się znikąd. Możemy go łatwo wyprowadzić, korzystając z niezawodnego twierdzenia Pitagorasa. Pokażę Ci, jak to zrobić, krok po kroku.-
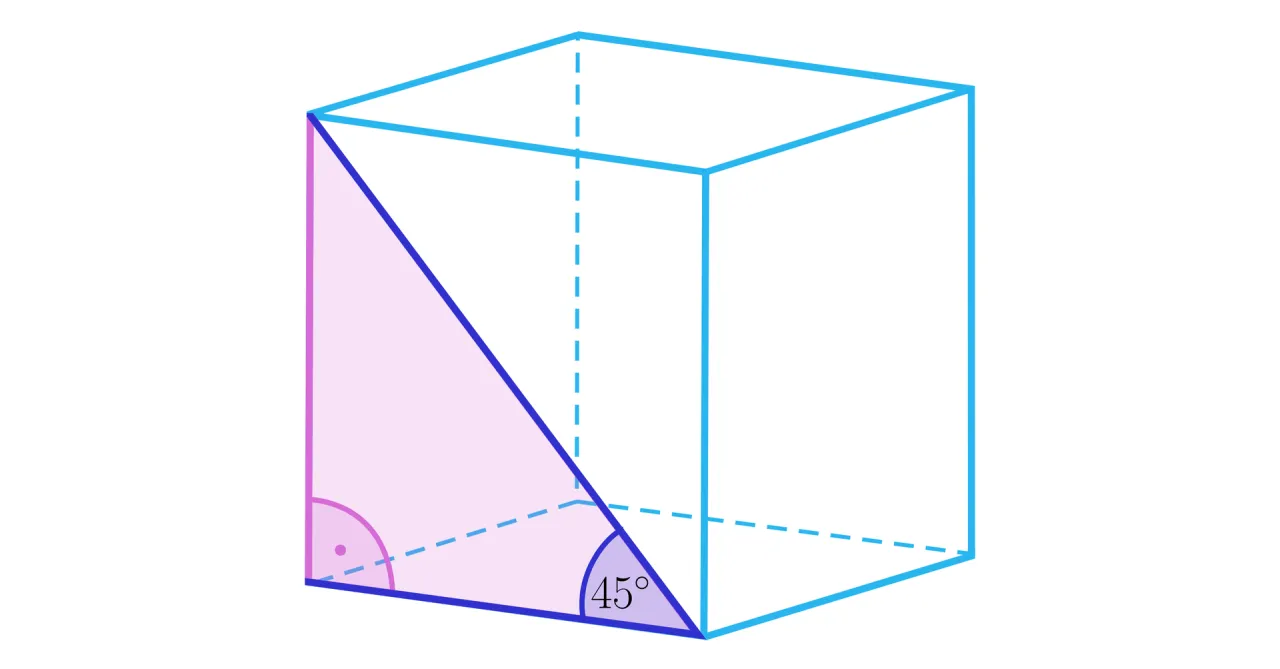
Krok 1: Obliczamy przekątną podstawy (ściany)
Pierwszym krokiem jest obliczenie długości przekątnej jednej ze ścian sześcianu. Ponieważ ściany sześcianu są kwadratami o boku a, możemy zastosować twierdzenie Pitagorasa do dowolnej takiej ściany. Przekątna kwadratu o boku a (oznaczmy ją jako p) wynosi:
p² = a² + a²
p² = 2a²
p = √(2a²) = a√2
Zapamiętaj ten wzór, bo przekątna kwadratu (a√2) jest często mylona z przekątną sześcianu!
-
Krok 2: Budujemy trójkąt prostokątny wewnątrz sześcianu i stosujemy twierdzenie Pitagorasa
Teraz, gdy znamy długość przekątnej podstawy (p = a√2), możemy utworzyć kolejny trójkąt prostokątny, który pozwoli nam znaleźć przekątną sześcianu (d). Ten trójkąt składa się z:
- jednej przyprostokątnej, którą jest przekątna podstawy (p),
- drugiej przyprostokątnej, którą jest krawędź sześcianu (a) wychodząca z wierzchołka, do którego dochodzi przekątna podstawy,
- przeciwprostokątnej, którą jest właśnie przekątna sześcianu (d).
Zastosujmy twierdzenie Pitagorasa do tego trójkąta:
d² = p² + a²
Podstawiamy teraz p = a√2:
d² = (a√2)² + a²
d² = 2a² + a²
d² = 3a²
Aby znaleźć d, pierwiastkujemy obie strony równania:
d = √(3a²)
d = a√3
I tak oto wyprowadziliśmy wzór na przekątną sześcianu. Proste, prawda?
Zadanie praktyczne: Oblicz przekątną sześcianu o krawędzi 5 cm
Przyjrzyjmy się konkretnemu przykładowi, aby utrwalić wiedzę. Obliczmy przekątną sześcianu, którego krawędź ma długość 5 cm.
- Dane: Długość krawędzi sześcianu a = 5 cm.
- Szukane: Długość przekątnej sześcianu d.
- Wzór: d = a√3.
- Obliczenia: Podstawiamy wartość a do wzoru: d = 5√3 cm.
- Odpowiedź: Przekątna sześcianu o krawędzi 5 cm wynosi 5√3 cm.
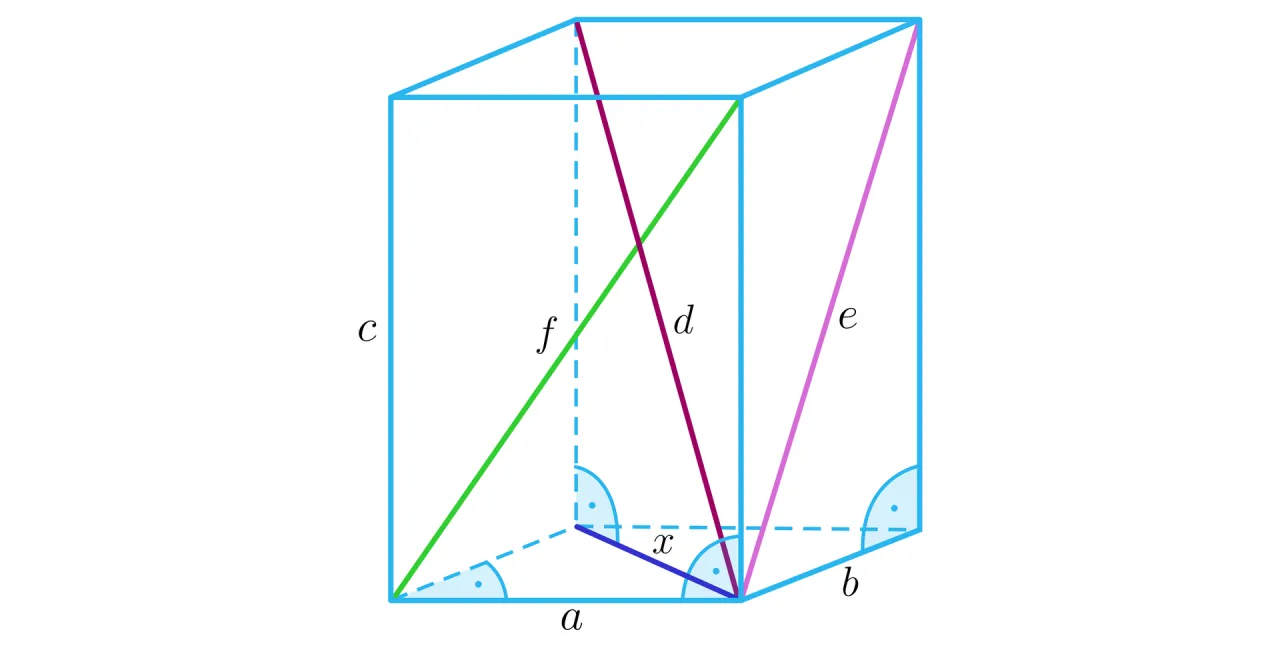
Przekątna prostopadłościanu: jak ją obliczyć?
Prostopadłościan to nieco bardziej złożona bryła, ponieważ jego krawędzie mogą mieć różne długości. Mamy tu trzy wymiary: długość, szerokość i wysokość. Oznaczamy je zazwyczaj jako a, b i c. Na szczęście, istnieje jeden uniwersalny wzór na przekątną prostopadłościanu, który działa niezależnie od wymiarów:
d = √(a² + b² + c²)
Gdzie:
- d to długość przekątnej prostopadłościanu (przekątnej bryły).
- a, b, c to długości krawędzi prostopadłościanu wychodzących z jednego wierzchołka.
Jak wyprowadzić wzór na przekątną prostopadłościanu? Metoda dwóch kroków
Wzór na przekątną prostopadłościanu również wyprowadzamy, dwukrotnie stosując twierdzenie Pitagorasa. To bardzo podobna metoda do tej, którą zastosowaliśmy dla sześcianu.
-
Krok 1: Wyznaczamy długość przekątnej prostokątnej podstawy
Najpierw musimy obliczyć długość przekątnej podstawy prostopadłościanu. Podstawa jest prostokątem o bokach a i b. Stosując twierdzenie Pitagorasa do tego prostokąta (oznaczmy przekątną podstawy jako p_p), otrzymujemy:
p_p² = a² + b²
p_p = √(a² + b²)
-
Krok 2: Ponownie korzystamy z twierdzenia Pitagorasa dla trójwymiarowej bryły
Teraz tworzymy trójkąt prostokątny wewnątrz prostopadłościanu. Jego wierzchołkami są:
- jeden wierzchołek podstawy,
- przeciwległy wierzchołek podstawy (połączony z pierwszym przez p_p),
- wierzchołek na górnej ścianie, leżący bezpośrednio nad pierwszym wierzchołkiem.
Boki tego trójkąta to:
- jedna przyprostokątna: przekątna podstawy (p_p),
- druga przyprostokątna: krawędź c (wysokość prostopadłościanu),
- przeciwprostokątna: przekątna prostopadłościanu (d).
Zastosujmy twierdzenie Pitagorasa:
d² = p_p² + c²
Podstawiamy p_p = √(a² + b²) do równania:
d² = (√(a² + b²))² + c²
d² = a² + b² + c²
Aby znaleźć d, pierwiastkujemy obie strony:
d = √(a² + b² + c²)
I tak oto mamy wzór na przekątną prostopadłościanu. Widzisz, że to nic skomplikowanego, jeśli rozłożysz problem na mniejsze części.
Zadanie praktyczne: Oblicz przekątną prostopadłościanu o wymiarach 3 cm x 4 cm x 5 cm
Przejdźmy do praktycznego zastosowania wzoru na przekątną prostopadłościanu. Obliczmy długość przekątnej bryły o podanych wymiarach.
- Dane: Długości krawędzi prostopadłościanu a = 3 cm, b = 4 cm, c = 5 cm.
- Szukane: Długość przekątnej prostopadłościanu d.
- Wzór: d = √(a² + b² + c²).
-
Obliczenia: Podstawiamy wartości do wzoru:
d = √(3² + 4² + 5²)
d = √(9 + 16 + 25)
d = √50
Możemy uprościć pierwiastek: √50 = √(25 * 2) = 5√2.
- Odpowiedź: Przekątna prostopadłościanu o wymiarach 3 cm x 4 cm x 5 cm wynosi 5√2 cm.
Obliczenia odwrotne: jak znaleźć krawędź, znając przekątną?
Często w zadaniach matematycznych spotykamy się z sytuacją, gdzie zamiast obliczać przekątną, znając boki, musimy zrobić coś odwrotnego: obliczyć długość krawędzi, mając daną przekątną. To świetny sposób na sprawdzenie, czy naprawdę rozumiesz wzory i potrafisz nimi manipulować.
Twoim danym jest przekątna sześcianu? Oto jak obliczyć jego krawędź
Jeśli znasz długość przekątnej sześcianu (d), możesz łatwo obliczyć długość jego krawędzi (a). Wystarczy przekształcić nasz podstawowy wzór d = a√3. Dzieląc obie strony przez √3, otrzymujemy:
a = d/√3
Pamiętaj, że często w mianowniku nie zostawia się pierwiastka, więc możesz pomnożyć licznik i mianownik przez √3, aby usunąć pierwiastek z mianownika: a = (d√3)/3.
Przykład: Przekątna sześcianu ma długość 10√3. Jaka jest długość jego boku i objętość?
Rozwiążmy zadanie, w którym dana jest przekątna sześcianu.
- Dane: Długość przekątnej sześcianu d = 10√3.
- Szukane: Długość krawędzi a i objętość V.
-
Obliczenia długości krawędzi:
Używamy przekształconego wzoru: a = d/√3.
a = (10√3)/√3
a = 10 cm
-
Obliczenia objętości:
Wzór na objętość sześcianu to V = a³.
V = 10³
V = 1000 cm³
- Odpowiedź: Długość boku sześcianu wynosi 10 cm, a jego objętość to 1000 cm³.
Masz daną przekątną prostopadłościanu? Sprawdź, jak poradzić sobie z obliczeniem krawędzi
W przypadku prostopadłościanu sytuacja jest nieco bardziej skomplikowana. Znając tylko długość przekątnej prostopadłościanu (d), nie jesteśmy w stanie jednoznacznie wyznaczyć wszystkich trzech długości krawędzi (a, b, c). Dzieje się tak, ponieważ mamy jedno równanie (d² = a² + b² + c²) i trzy niewiadome. Potrzebujemy dodatkowych informacji, aby rozwiązać taki problem.
Analiza przypadku: Czy zawsze da się obliczyć wszystkie krawędzie prostopadłościanu, znając tylko jego przekątną?
Jak wspomniałem, odpowiedź brzmi: nie, nie zawsze. Aby móc obliczyć wszystkie krawędzie, musisz mieć dodatkowe dane. Może to być informacja o stosunkach między krawędziami (np. a = 2b i c = 3b) lub o tym, że prostopadłościan ma jakieś szczególne właściwości (np. jest sześcianem, czyli a = b = c, co sprowadza problem do przypadku sześcianu). Bez takich informacji, z samej długości przekątnej możesz co najwyżej stwierdzić, że suma kwadratów długości krawędzi musi być równa kwadratowi długości przekątnej.
Unikaj pułapek: najczęstsze błędy przy obliczaniu przekątnych
Jako osoba z doświadczeniem w nauczaniu, wiem, że pewne błędy powtarzają się nagminnie. Chcę Ci pomóc ich uniknąć, dlatego zebrałem najczęstsze pułapki, na które warto uważać.
Błąd nr 1: Mylenie wzoru na przekątną sześcianu (a√3) z przekątną kwadratu (a√2)
To absolutnie najczęstszy błąd! Wielu uczniów automatycznie używa wzoru a√2, który jest poprawny dla przekątnej kwadratu (czyli przekątnej ściany sześcianu), ale nie dla przekątnej całej bryły. Pamiętaj, że a√2 dotyczy figury dwuwymiarowej (kwadratu), a a√3 dotyczy bryły trójwymiarowej (sześcianu). Różnica jest subtelna, ale fundamentalna!
Błąd nr 2: Niepoprawne podnoszenie do kwadratu w twierdzeniu Pitagorasa
Kolejnym źródłem problemów są błędy algebraiczne, zwłaszcza przy podnoszeniu do kwadratu wyrażeń zawierających pierwiastki. Na przykład, (a√2)² to nie a²√2, lecz a² * (√2)² = a² * 2 = 2a². Upewnij się, że poprawnie stosujesz zasady potęgowania i pierwiastkowania, aby uniknąć błędów w dalszych obliczeniach.
Błąd nr 3: Złe jednostki dlaczego spójność jest kluczem do poprawnego wyniku
Zawsze upewnij się, że wszystkie długości, które podstawiasz do wzorów, są wyrażone w tych samych jednostkach. Jeśli jedna krawędź jest podana w centymetrach, a druga w metrach, musisz najpierw przeliczyć je na wspólną jednostkę. Mieszanie jednostek (np. cm z m) bez konwersji doprowadzi do błędnego wyniku. Spójność jednostek to podstawa w każdym zadaniu matematycznym i fizycznym.Twoja ściągawka: najważniejsze wzory na przekątne
Aby ułatwić Ci zapamiętanie kluczowych informacji, przygotowałem krótkie podsumowanie najważniejszych wzorów. Potraktuj to jako swoją szybką ściągawkę.
Sześcian: Kiedy używać a√3, a kiedy a√2?
- Przekątna bryły (sześcianu): d = a√3 (łączy dwa najbardziej oddalone wierzchołki, nieleżące na tej samej ścianie).
- Przekątna ściany (kwadratu): p = a√2 (łączy przeciwległe wierzchołki na tej samej ścianie).
Przeczytaj również: Jak obliczyć pole trapezu prostokątnego? Wzór, Pitagoras i kroki
Prostopadłościan: Jeden wzór, który rozwiązuje wszystkie problemy
Dla prostopadłościanu masz jeden uniwersalny wzór na przekątną bryły, który zawsze działa, niezależnie od wymiarów: d = √(a² + b² + c²). Pamiętaj, że a, b i c to długości krawędzi wychodzących z jednego wierzchołka.

