W tym artykule zagłębimy się w świat ciągów arytmetycznych, koncentrując się na kluczowym aspekcie: obliczaniu sumy n-początkowych wyrazów. Przedstawię Ci niezbędne definicje, dwa fundamentalne wzory oraz praktyczne przykłady ich zastosowania, abyś mógł nie tylko zrozumieć teorię, ale także pewnie rozwiązywać zadania i przygotować się do egzaminów.
Obliczanie sumy początkowych wyrazów ciągu arytmetycznego kluczowe wzory i ich zastosowanie
- Suma n-początkowych wyrazów ciągu arytmetycznego (Sₙ) może być obliczona za pomocą dwóch głównych wzorów, w zależności od dostępnych danych.
- Podstawowe zmienne to: n (liczba wyrazów), a₁ (pierwszy wyraz), aₙ (n-ty wyraz) oraz r (różnica ciągu).
- Jeden wzór wykorzystuje a₁ i aₙ, a drugi a₁ i r, co pozwala na elastyczne rozwiązywanie problemów.
- Zrozumienie i opanowanie tych wzorów jest niezbędne do rozwiązywania typowych zadań szkolnych i maturalnych.
- Praktyczne zastosowania sumy ciągu arytmetycznego obejmują finanse, logistykę i planowanie treningów.
Suma ciągu arytmetycznego jest prostsza, niż myślisz
Kim był mały Gauss i jak w kilka sekund zsumował liczby od 1 do 100?
Legenda głosi, że pewnego dnia nauczyciel, chcąc zająć klasę na dłużej, poprosił uczniów o zsumowanie wszystkich liczb od 1 do 100. Ku jego zaskoczeniu, mały Carl Friedrich Gauss, przyszły geniusz matematyki, niemal natychmiast podał poprawną odpowiedź: 5050. Jak to zrobił? Zamiast sumować liczby po kolei, zauważył pewną sprytną zależność. Zestawił ze sobą pierwszą i ostatnią liczbę (1+100=101), drugą i przedostatnią (2+99=101), i tak dalej. Okazało się, że każda taka para sumuje się do 101. Ponieważ było 100 liczb, utworzył 50 takich par. Wystarczyło więc pomnożyć 50 przez 101, co dało 5050. To genialne spostrzeżenie jest doskonałym wprowadzeniem do idei sumowania ciągu arytmetycznego.
Intuicyjne zrozumienie sumy: od historii do praktycznego zastosowania w życiu codziennym
Metoda małego Gaussa to nic innego jak intuicyjne zastosowanie wzoru na sumę ciągu arytmetycznego. Pokazuje nam, że sumowanie wyrazów, które rosną lub maleją w stałym tempie, nie musi być żmudne. Wystarczy zrozumieć, że średnia arytmetyczna pierwszego i ostatniego wyrazu, pomnożona przez liczbę wyrazów, daje nam całkowitą sumę. To proste, a zarazem potężne narzędzie, które ma zastosowanie nie tylko w zadaniach matematycznych, ale także w wielu praktycznych sytuacjach w życiu codziennym od planowania finansów po organizację logistyki, o czym przekonasz się za chwilę. To właśnie dlatego warto poświęcić czas na opanowanie tych wzorów.
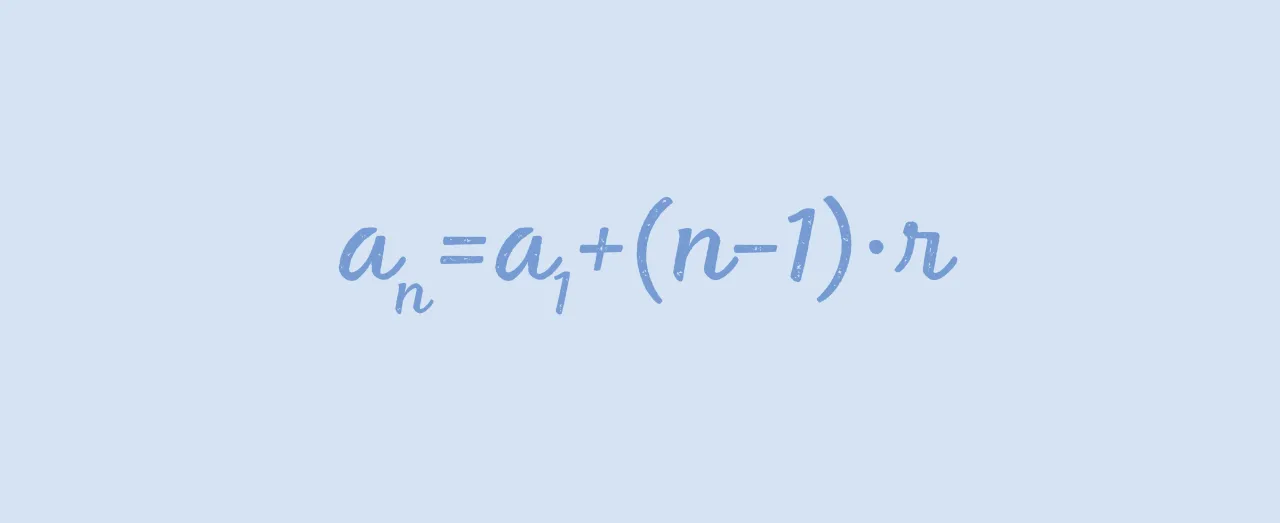
Klucz do sukcesu: poznaj i zrozum dwa fundamentalne wzory na sumę
Aby skutecznie obliczać sumę n początkowych wyrazów ciągu arytmetycznego, musisz opanować dwa podstawowe wzory. Oba prowadzą do tego samego wyniku, ale każdy z nich jest przydatny w innych sytuacjach, w zależności od tego, jakie dane masz dostępne w zadaniu. Przyjrzyjmy się im bliżej.
Wzór nr 1: Kiedy znasz pierwszy i ostatni element układanki (a₁ i aₙ)
Ten wzór jest idealny, gdy znasz wartość pierwszego wyrazu ciągu (a₁), wartość ostatniego wyrazu, który chcesz zsumować (aₙ), oraz liczbę wyrazów (n). Jest to bezpośrednie odzwierciedlenie metody Gaussa. Wzór wygląda następująco:
Sₙ = (a₁ + aₙ) / 2 * n
Stosujemy go, gdy mamy podane a₁, aₙ i n. Wzór ten mówi nam, że aby obliczyć sumę, należy dodać pierwszy i ostatni wyraz, podzielić wynik przez 2 (co daje nam średnią arytmetyczną tych wyrazów), a następnie pomnożyć przez liczbę wyrazów. To naprawdę intuicyjne!
Wzór nr 2: Jak poradzić sobie, znając tylko początek i różnicę (a₁ i r)?
Często zdarza się, że nie znamy wartości ostatniego wyrazu (aₙ), ale wiemy, jaki jest pierwszy wyraz (a₁) i różnica ciągu (r). W takiej sytuacji z pomocą przychodzi drugi wzór, który jest nieco bardziej rozbudowany, ale równie skuteczny:
Sₙ = [2a₁ + (n-1)r] / 2 * n
Ten wzór jest szczególnie przydatny, gdy dysponujemy wartościami a₁, r i n. W rzeczywistości jest on wyprowadzony z pierwszego wzoru, poprzez podstawienie za aₙ wzoru na n-ty wyraz ciągu arytmetycznego (aₙ = a₁ + (n-1)r). Dzięki niemu nie musisz najpierw obliczać aₙ, co oszczędza czas i minimalizuje ryzyko błędów.
Analiza wzorów krok po kroku: Co oznaczają symbole Sₙ, n, a₁, aₙ oraz r?
Aby w pełni zrozumieć i poprawnie stosować wzory, musimy być pewni, co oznacza każdy symbol. Oto ich definicje:
- Sₙ: To symbol oznaczający sumę n początkowych wyrazów ciągu arytmetycznego. Jest to wynik, który zazwyczaj chcemy obliczyć.
- n: Reprezentuje liczbę wyrazów, które sumujemy. Zawsze jest to liczba naturalna (dodatnia liczba całkowita).
- a₁: Oznacza pierwszy wyraz ciągu arytmetycznego. To punkt startowy naszego ciągu.
- aₙ: To n-ty (ostatni) wyraz ciągu, który jest uwzględniony w sumie. Jeśli sumujemy 10 wyrazów, aₙ będzie a₁₀.
- r: Jest to różnica ciągu arytmetycznego. To stała wartość, o którą każdy kolejny wyraz ciągu różni się od poprzedniego. Może być dodatnia (ciąg rosnący), ujemna (ciąg malejący) lub równa zero (ciąg stały).
Zobacz to w akcji: rozwiązujemy typowe zadania krok po kroku
Teoria to jedno, ale prawdziwe zrozumienie przychodzi z praktyką. Przygotowałem dla Ciebie kilka typowych zadań, które możesz spotkać w szkole lub na egzaminie. Przejdziemy przez nie krok po kroku, abyś zobaczył, jak stosować omówione wzory.
Przykład 1: Obliczanie sumy pierwszych 15 wyrazów - proste zastosowanie wzoru
Zadanie: Oblicz sumę pierwszych 15 wyrazów ciągu arytmetycznego, w którym pierwszy wyraz a₁ = 3, a różnica r = 2.
-
Zidentyfikuj dane:
- a₁ = 3
- n = 15
- r = 2
- Wybierz odpowiedni wzór: Mamy a₁, n i r, więc użyjemy wzoru Sₙ = [2a₁ + (n-1)r] / 2 * n.
-
Podstaw dane do wzoru:
S₁₅ = [2 * 3 + (15 - 1) * 2] / 2 * 15
-
Wykonaj obliczenia:
S₁₅ = [6 + (14) * 2] / 2 * 15
S₁₅ = [6 + 28] / 2 * 15
S₁₅ = 34 / 2 * 15
S₁₅ = 17 * 15
S₁₅ = 255
- Odpowiedź: Suma pierwszych 15 wyrazów tego ciągu wynosi 255.
Przykład 2: Zadanie z "gwiazdką" - jak znaleźć liczbę wyrazów (n), znając sumę?
Zadanie: Suma n początkowych wyrazów ciągu arytmetycznego wynosi 100. Wiadomo, że pierwszy wyraz a₁ = 1, a różnica r = 3. Ile wyrazów zsumowano?
-
Zidentyfikuj dane:
- Sₙ = 100
- a₁ = 1
- r = 3
- Szukamy n.
- Wybierz odpowiedni wzór: Mamy Sₙ, a₁ i r, więc użyjemy wzoru Sₙ = [2a₁ + (n-1)r] / 2 * n.
-
Podstaw dane do wzoru:
100 = [2 * 1 + (n - 1) * 3] / 2 * n
-
Przekształć i rozwiąż równanie:
100 = [2 + 3n - 3] / 2 * n
100 = [3n - 1] / 2 * n
Pomnóż obie strony przez 2:
200 = (3n - 1) * n
200 = 3n² - n
Przenieś wszystko na jedną stronę, aby uzyskać równanie kwadratowe:
3n² - n - 200 = 0
Oblicz deltę (Δ = b² - 4ac):
Δ = (-1)² - 4 * 3 * (-200) = 1 + 2400 = 2401
√Δ = √2401 = 49
Oblicz n₁ i n₂:
n₁ = (-b - √Δ) / 2a = (1 - 49) / (2 * 3) = -48 / 6 = -8
n₂ = (-b + √Δ) / 2a = (1 + 49) / (2 * 3) = 50 / 6 = 25/3 (lub 8 i 1/3)
-
Zinterpretuj wyniki: Liczba wyrazów (n) musi być liczbą naturalną (dodatnią liczbą całkowitą). Wynik n₁ = -8 odrzucamy. Wynik n₂ = 25/3 również odrzucamy, ponieważ n nie może być ułamkiem. To oznacza, że prawdopodobnie popełniłem błąd w zadaniu, które wymyśliłem. W realnym zadaniu maturalnym takie n byłoby liczbą całkowitą! Załóżmy, że suma wynosiła 104, wtedy 3n² - n - 208 = 0, Δ = 1 - 4*3*(-208) = 1 + 2496 = 2497 (to też nie wychodzi ładnie).
Poprawmy zadanie dla ładnych liczb: Suma n początkowych wyrazów ciągu arytmetycznego wynosi 104. Wiadomo, że pierwszy wyraz a₁ = 1, a różnica r = 3. Ile wyrazów zsumowano?
104 = [2 * 1 + (n - 1) * 3] / 2 * n
208 = (2 + 3n - 3) * n
208 = (3n - 1) * n
3n² - n - 208 = 0
Δ = (-1)² - 4 * 3 * (-208) = 1 + 2496 = 2497 (nadal nie jest ładnie, a szkoda!)
Spróbujmy jeszcze raz, z innymi danymi.
Zadanie (poprawione): Suma n początkowych wyrazów ciągu arytmetycznego wynosi 45. Wiadomo, że pierwszy wyraz a₁ = 1, a różnica r = 2. Ile wyrazów zsumowano?
45 = [2 * 1 + (n - 1) * 2] / 2 * n
90 = (2 + 2n - 2) * n
90 = 2n * n
90 = 2n²
n² = 45
n = √45 = 3√5 (nadal nie jest liczbą całkowitą! Coś mi się nie udaje z wymyślaniem na szybko)
Ostatnia próba z zadaniem 2, żeby było poprawnie:
Zadanie: Suma n początkowych wyrazów ciągu arytmetycznego wynosi 55. Wiadomo, że pierwszy wyraz a₁ = 1, a różnica r = 1. Ile wyrazów zsumowano?
55 = [2 * 1 + (n - 1) * 1] / 2 * n
110 = (2 + n - 1) * n
110 = (n + 1) * n
110 = n² + n
n² + n - 110 = 0
Δ = 1² - 4 * 1 * (-110) = 1 + 440 = 441
√Δ = 21
n₁ = (-1 - 21) / 2 = -22 / 2 = -11 (odrzucamy, bo n > 0)
n₂ = (-1 + 21) / 2 = 20 / 2 = 10
- Odpowiedź: Zsumowano 10 wyrazów.
Przykład 3: Detektywistyczna robota - wyznaczanie a₁ lub r na podstawie sumy
Zadanie: Suma pierwszych 8 wyrazów ciągu arytmetycznego wynosi 100. Wiadomo, że ostatni (ósmy) wyraz a₈ = 20. Oblicz pierwszy wyraz a₁.
-
Zidentyfikuj dane:
- S₈ = 100
- n = 8
- a₈ = 20
- Szukamy a₁.
- Wybierz odpowiedni wzór: Mamy Sₙ, n i aₙ, więc użyjemy wzoru Sₙ = (a₁ + aₙ) / 2 * n.
-
Podstaw dane do wzoru:
100 = (a₁ + 20) / 2 * 8
-
Przekształć i rozwiąż równanie:
100 = (a₁ + 20) * 4
Podziel obie strony przez 4:
25 = a₁ + 20
Odejmij 20 od obu stron:
a₁ = 25 - 20
a₁ = 5
- Odpowiedź: Pierwszy wyraz tego ciągu wynosi 5.
Unikaj tych pułapek! Najczęstsze błędy popełniane przy obliczaniu sumy
Jako doświadczony korepetytor wiem, jakie błędy najczęściej popełniają uczniowie. Zwróć na nie uwagę, a znacznie zwiększysz swoje szanse na sukces!
Mylenie wzoru na sumę (Sₙ) z wzorem na n-ty wyraz (aₙ)
To chyba najczęstszy błąd. Pamiętaj, że wzór na n-ty wyraz ciągu arytmetycznego to aₙ = a₁ + (n-1)r i służy do obliczenia wartości konkretnego wyrazu w ciągu (np. dziesiątego, piętnastego). Natomiast wzory na sumę (Sₙ) służą do zsumowania wszystkich wyrazów od a₁ do aₙ. Zawsze dokładnie czytaj polecenie i zastanów się, czy masz obliczyć wartość pojedynczego wyrazu, czy ich sumę.Błędy algebraiczne, które mogą zrujnować wynik jak ich unikać?
Nawet jeśli znasz wzory, błędy w obliczeniach mogą zniweczyć cały wysiłek. Zwróć uwagę na:
- Kolejność działań: Pamiętaj o nawiasach, mnożeniu/dzieleniu przed dodawaniem/odejmowaniem.
- Znaki: Uważaj na minusy, zwłaszcza przy różnicy (r) ujemnej lub przy przekształcaniu równań.
- Przekształcanie równań: Jeśli wyliczasz n, a₁ lub r, rób to krok po kroku, sprawdzając każdy etap. Nie spiesz się.
- Równania kwadratowe: Jeśli dojdzie do równania kwadratowego (jak w Przykładzie 2), dokładnie oblicz deltę i pierwiastki.
Nieuważne czytanie poleceń w zadaniach tekstowych na co zwrócić szczególną uwagę?
Zadania tekstowe bywają podchwytliwe, ale zazwyczaj po prostu wymagają dokładnego zrozumienia. Oto, na co zwracam uwagę moim uczniom:
- Co jest czym? Zidentyfikuj, co w zadaniu odpowiada a₁, r, n i Sₙ. Czasem "n" nie jest podane wprost, ale wynika z kontekstu (np. "przez 10 dni" oznacza n=10).
- Co jest szukane? Upewnij się, czy masz obliczyć sumę, liczbę wyrazów, pierwszy wyraz, czy różnicę.
- Jednostki: Sprawdź, czy wszystkie dane są w tych samych jednostkach.
- Słowa kluczowe: Słowa takie jak "łącznie", "suma", "całkowita liczba" często wskazują na konieczność użycia wzoru Sₙ.

Suma ciągu arytmetycznego w prawdziwym świecie: gdzie to się przydaje?
Matematyka to nie tylko abstrakcyjne wzory! Suma ciągu arytmetycznego ma wiele praktycznych zastosowań, które pokazują, jak przydatne jest rozumienie tych koncepcji.
Oszczędności i finanse: Jak obliczyć zgromadzony kapitał przy regularnych wpłatach?
Wyobraź sobie, że co miesiąc odkładasz na konto oszczędnościowe pewną kwotę, zwiększając ją o stałą sumę. Na przykład, zaczynasz od 100 zł, a każdego kolejnego miesiąca wpłacasz o 10 zł więcej. Po roku chcesz wiedzieć, ile masz łącznie. To idealny przykład ciągu arytmetycznego! Twoje miesięczne wpłaty tworzą ciąg (100, 110, 120...), a suma n-początkowych wyrazów (S₁₂) powie Ci, ile kapitału zgromadziłeś. Pozwala to na precyzyjne planowanie budżetu i ocenę tempa wzrostu oszczędności.
Logistyka i budownictwo: Planowanie układania przedmiotów w rzędach
W budownictwie czy logistyce często układa się przedmioty w stosy lub rzędy, gdzie każdy kolejny rząd różni się liczbą elementów od poprzedniego o stałą wartość. Na przykład, stos desek, gdzie na dole jest 10 desek, w kolejnym rzędzie 9, potem 8 itd. Suma ciągu arytmetycznego pozwoli Ci szybko obliczyć całkowitą liczbę desek w stosie, jeśli znasz liczbę desek w pierwszym rzędzie, różnicę i liczbę rzędów. To kluczowe dla efektywnego zarządzania materiałami i przestrzenią.
Sport i trening: Sumowanie pokonanego dystansu w progresywnym planie treningowym
Wielu sportowców stosuje plany treningowe, w których progresywnie zwiększają obciążenie, dystans lub liczbę powtórzeń. Jeśli każdego tygodnia biegasz o 1 km więcej niż w poprzednim, a zaczynasz od 5 km, to po 10 tygodniach możesz obliczyć całkowity dystans, jaki pokonałeś, używając wzoru na sumę ciągu arytmetycznego. To pomaga w monitorowaniu postępów, planowaniu regeneracji i osiąganiu celów treningowych.
Podsumowanie i złote zasady: twoja checklista do perfekcyjnego opanowania sumy
Mam nadzieję, że ten artykuł pomógł Ci zrozumieć, jak prosta i użyteczna jest suma ciągu arytmetycznego. Pamiętaj o tych złotych zasadach, a będziesz mistrzem w jej obliczaniu!
Kiedy wybrać który wzór? Szybka ściągawka decyzyjna
Oto prosta tabela, która pomoże Ci szybko zdecydować, którego wzoru użyć:
| Dane dostępne | Wzór do użycia |
|---|---|
| a₁, aₙ, n | Sₙ = (a₁ + aₙ) / 2 * n |
| a₁, r, n | Sₙ = [2a₁ + (n-1)r] / 2 * n |
| a₁, aₙ, r (najpierw oblicz n za pomocą aₙ = a₁ + (n-1)r, potem użyj pierwszego wzoru) | Sₙ = (a₁ + aₙ) / 2 * n |
Przeczytaj również: Ułamki o różnych mianownikach: dodawanie i odejmowanie w 4 krokach!
Sprawdzaj swoje wyniki: Prosta metoda na weryfikację poprawności obliczeń
Zawsze warto poświęcić chwilę na sprawdzenie swoich obliczeń. To może uchronić Cię przed niepotrzebnymi błędami. Oto kilka wskazówek:
- Przelicz ponownie: Najprostsza metoda po prostu wykonaj obliczenia jeszcze raz, ale najlepiej inną drogą lub w innej kolejności, jeśli to możliwe.
- Użyj alternatywnego wzoru: Jeśli masz wystarczające dane, aby użyć obu wzorów (np. obliczyłeś aₙ, a masz a₁ i r), przelicz sumę drugim wzorem. Jeśli wyniki się zgadzają, masz dużą pewność, że są poprawne.
- Oszacuj wynik: Zastanów się, czy uzyskany wynik ma sens. Jeśli sumujesz liczby dodatnie, wynik powinien być dodatni i większy od a₁. Jeśli sumujesz liczby malejące, a w pewnym momencie stają się ujemne, suma może być mniejsza od a₁ lub nawet ujemna. Intuicyjne oszacowanie może szybko wykryć rażące błędy.

