Nierówności z wartością bezwzględną to jeden z tych tematów w matematyce, które często sprawiają uczniom trudność, a jednocześnie są niezwykle ważne zwłaszcza w kontekście egzaminu maturalnego czy dalszej nauki. Zrozumienie, czym jest wartość bezwzględna i jak ją interpretować, to klucz do skutecznego rozwiązywania zadań, które na pierwszy rzut oka mogą wydawać się skomplikowane. W tym kompleksowym poradniku przeprowadzę Cię krok po kroku przez różne typy nierówności z wartością bezwzględną, pokażę skuteczne metody ich rozwiązywania oraz wskażę, na co zwrócić szczególną uwagę, aby uniknąć typowych błędów.
Rozwiązywanie nierówności z wartością bezwzględną: klucz do sukcesu na maturze i w nauce matematyki
- Wartość bezwzględna to odległość liczby od zera lub od innej liczby na osi.
- Dwa główne typy nierówności: `|wyrażenie| < a` (koniunkcja) i `|wyrażenie| > a` (alternatywa).
- Stosuj metody: algebraiczną (przez definicję), geometryczną (na osi) lub analizę przypadków (dla wielu modułów).
- Kluczowe jest poprawne przekształcanie nierówności i wizualizacja rozwiązań na osi liczbowej.
- Pamiętaj o założeniach dla niewiadomej poza modułem i o przypadkach szczególnych (zero/liczba ujemna po prawej stronie).
- Unikaj najczęstszych błędów, takich jak mylenie "i" z "lub" czy błędna zmiana znaku.
Zrozumienie wartości bezwzględnej: klucz do nierówności
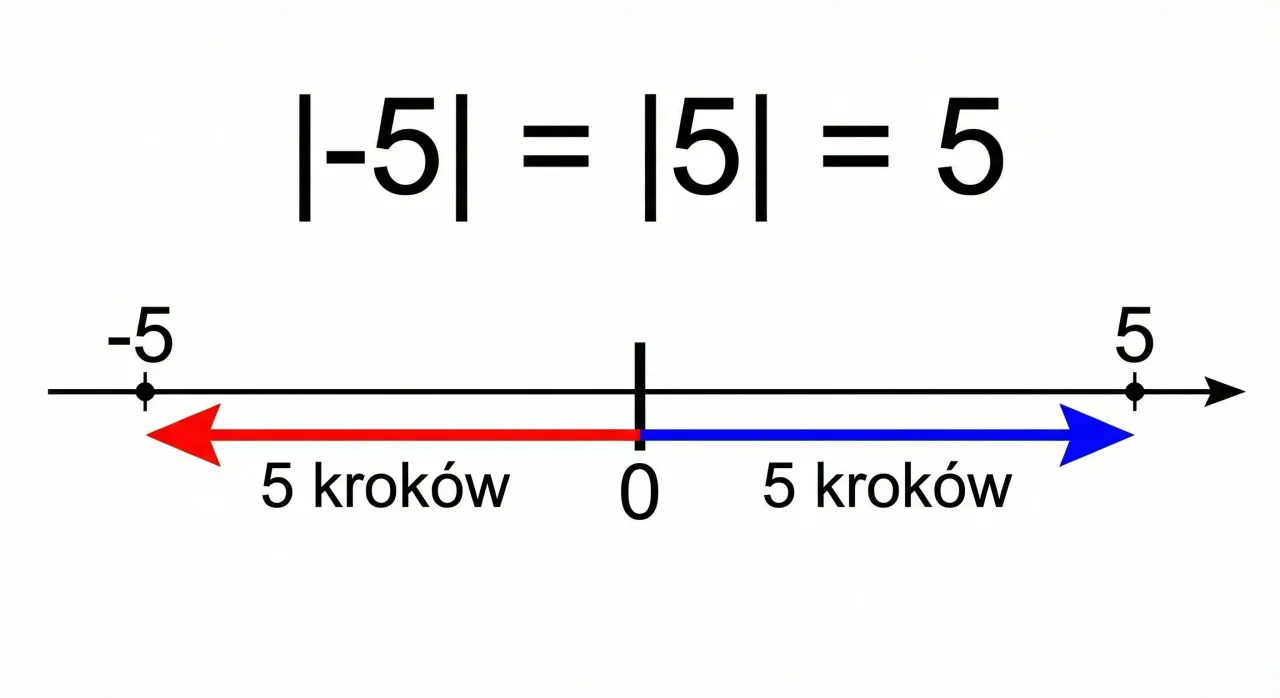
Zanim zagłębimy się w świat nierówności, musimy upewnić się, że solidnie rozumiemy samo pojęcie wartości bezwzględnej. Algebraicznie, wartość bezwzględna liczby \(x\), oznaczana jako \(|x|\), jest definiowana w dwojaki sposób: jeśli \(x \geq 0\), to \(|x| = x\); jeśli natomiast \(x < 0\), to \(|x| = -x\). Oznacza to, że wartość bezwzględna zawsze zwraca liczbę nieujemną, "usuwając" znak minus, jeśli liczba jest ujemna.
Jednak dla mnie, jako praktyka, najbardziej intuicyjna jest interpretacja geometryczna. Wartość bezwzględna \(|x-a|\) oznacza po prostu odległość liczby \(x\) od liczby \(a\) na osi liczbowej. Na przykład, \(|x-3|\) to odległość \(x\) od \(3\). Zrozumienie tej koncepcji jest fundamentalne, ponieważ pozwala nam wizualizować problem i często znacznie ułatwia zrozumienie, czego właściwie szukamy w rozwiązaniu nierówności.
Rozpoznaj i rozwiąż dwa główne typy nierówności
Większość nierówności z wartością bezwzględną, z którymi spotkasz się na początkowym etapie nauki, można sprowadzić do dwóch podstawowych typów. Kluczowe jest, abyś potrafił je rozpoznać i wiedział, jak do nich podejść. Od tego zależy, czy zastosujesz koniunkcję ("i"), czy alternatywę ("lub") w dalszych krokach rozwiązania.
Pierwszy typ to nierówności, w których wartość bezwzględna jest mniejsza od pewnej liczby dodatniej (np. \(|wyrażenie| < a\)). Drugi typ to te, w których wartość bezwzględna jest większa od pewnej liczby dodatniej (np. \(|wyrażenie| > a\)). Omówmy je szczegółowo, bo to właśnie tutaj najczęściej pojawiają się pierwsze błędy.
Nierówność typu |x - a| < b: szukanie liczb "blisko" punktu a
Kiedy widzisz nierówność typu \(|wyrażenie| < a\) (gdzie \(a > 0\)), powinieneś myśleć o liczbach, które są "blisko" pewnego punktu na osi. Geometrycznie oznacza to, że szukamy wszystkich \(x\), których odległość od punktu \(a\) jest mniejsza niż \(b\). Algebraicznie, taka nierówność jest równoważna koniunkcji: \( -a < wyrażenie < a\). Rozwiązywanie tego typu nierówności to proces, który można podzielić na kilka jasnych kroków:
-
Krok 1: Zastosowanie reguły i rozbicie na dwie nierówności
Pierwszym krokiem jest przekształcenie nierówności z wartością bezwzględną w układ dwóch prostszych nierówności. Nierówność \(|wyrażenie| < a\) staje się \(wyrażenie < a\) i \(wyrażenie > -a\). Możemy to zapisać jako podwójną nierówność: \( -a < wyrażenie < a\). Na przykład, jeśli masz \(|x-2| < 5\), przekształcasz to na \( -5 < x-2 < 5\).
-
Krok 2: Rozwiązanie układu nierówności i znalezienie części wspólnej
Po rozbiciu na dwie nierówności, rozwiązujesz każdą z nich osobno. Następnie, ponieważ połączyłeś je spójnikiem "i" (koniunkcja), musisz znaleźć część wspólną (iloczyn) zbiorów rozwiązań obu nierówności. Oznacza to, że szukasz liczb, które spełniają obie nierówności jednocześnie.
-
Krok 3: Zaznaczenie rozwiązania na osi liczbowej: wizualizacja wyniku
Wizualizacja jest kluczowa! Zawsze zaznaczaj swoje rozwiązania na osi liczbowej. Dla nierówności typu \(|wyrażenie| < a\), rozwiązaniem będzie zazwyczaj pojedynczy przedział. Pamiętaj o użyciu otwartych kółek (dla \(<\) i \(>\)) lub zamalowanych (dla \( \leq \) i \( \geq \)) na końcach przedziału, aby poprawnie odzwierciedlić, czy punkty krańcowe należą do rozwiązania.
Nierówność typu |x - a| > b: szukanie liczb "daleko" od punktu a
Drugi główny typ to nierówności postaci \(|wyrażenie| > a\) (gdzie \(a > 0\)). Tutaj myślimy o liczbach, które są "daleko" od pewnego punktu. Geometrycznie, szukamy \(x\), których odległość od punktu \(a\) jest większa niż \(b\). Algebraicznie, taka nierówność jest równoważna alternatywie: \(wyrażenie > a\) LUB \(wyrażenie < -a\). Oto jak postępować:
-
Krok 1: Przekształcenie na alternatywę dwóch prostych nierówności
Nierówność \(|wyrażenie| > a\) przekształcasz na dwie oddzielne nierówności połączone spójnikiem "LUB": \(wyrażenie > a\) LUB \(wyrażenie < -a\). Na przykład, jeśli masz \(|x+1| > 3\), rozbijasz to na \(x+1 > 3\) LUB \(x+1 < -3\).
-
Krok 2: Rozwiązanie każdej nierówności osobno
Rozwiązujesz każdą z tych dwóch nierówności niezależnie. Są to proste nierówności liniowe, które powinieneś już umieć rozwiązywać, przenosząc stałe na jedną stronę, a niewiadome na drugą.
-
Krok 3: Zsumowanie przedziałów jako ostateczny wynik
Ponieważ nierówności połączone są spójnikiem "LUB" (alternatywa), ostatecznym rozwiązaniem jest suma zbiorów rozwiązań obu nierówności. Oznacza to, że do rozwiązania należą wszystkie liczby, które spełniają pierwszą nierówność, drugą nierówność, lub obie. Na osi liczbowej będzie to zazwyczaj wyglądało jako dwa rozłączne przedziały.
Przeczytaj również: Jak wyznaczyć dziedzinę funkcji ze wzoru? Opanuj to!
Praktyczne przykłady rozwiązywania nierówności
Teoria to jedno, ale prawdziwe zrozumienie przychodzi z praktyką. Przyjrzyjmy się teraz kilku przykładom, które pozwolą Ci utrwalić omówione metody i zobaczyć, jak radzić sobie z różnymi scenariuszami.
Przykład 1: Klasyczna nierówność z jedną wartością bezwzględną
Rozwiążmy nierówność \(|2x - 4| \leq 6\).
Metoda algebraiczna: Ponieważ mamy znak \( \leq \), stosujemy koniunkcję: \( -6 \leq 2x - 4 \leq 6\) Rozbijamy na dwie nierówności: 1. \(2x - 4 \leq 6\) \(2x \leq 10\) \(x \leq 5\) 2. \(2x - 4 \geq -6\) \(2x \geq -2\) \(x \geq -1\) Szukamy części wspólnej rozwiązań \(x \leq 5\) i \(x \geq -1\). Rozwiązanie: \(x \in [-1, 5]\).
Metoda geometryczna: Nierówność \(|2x - 4| \leq 6\) możemy zapisać jako \(|2(x - 2)| \leq 6\), czyli \(2|x - 2| \leq 6\), co daje \(|x - 2| \leq 3\). Interpretujemy to jako: odległość liczby \(x\) od liczby \(2\) na osi liczbowej jest mniejsza lub równa \(3\). Zaczynamy od punktu \(2\). Idziemy o \(3\) jednostki w prawo (\(2+3=5\)) i o \(3\) jednostki w lewo (\(2-3=-1\)). Wszystkie liczby między \( -1 \) a \( 5 \) (włącznie z nimi) spełniają tę nierówność. Rozwiązanie: \(x \in [-1, 5]\). Na osi liczbowej zaznaczamy przedział od \( -1 \) do \( 5 \) z zamalowanymi kółkami na końcach.
Przykład 2: Gdy niewiadoma "x" pojawia się po obu stronach nierówności
Rozwiążmy nierówność \(|2x - 3| < x\).
W tym przypadku po prawej stronie nierówności mamy niewiadomą \(x\). Pamiętaj, że wartość bezwzględna jest zawsze nieujemna. Jeśli \(x\) po prawej stronie byłoby ujemne, nierówność \(|2x - 3| < x\) nie miałaby rozwiązań (np. \(|...| < -5\) jest niemożliwe). Dlatego pierwszym i kluczowym założeniem jest, że \(x > 0\). Bez tego założenia rozwiązanie będzie błędne.
Przy założeniu \(x > 0\), możemy zastosować standardową regułę dla nierówności typu \(|wyrażenie| < a\): \( -x < 2x - 3 < x\) Rozbijamy na dwie nierówności i rozwiązujemy je, pamiętając o założeniu \(x > 0\):
1. \(2x - 3 < x\) \(x < 3\)
2. \(2x - 3 > -x\) \(3x > 3\) \(x > 1\)
Musimy znaleźć część wspólną wszystkich warunków: \(x > 0\), \(x < 3\) i \(x > 1\). Nakładając je na oś liczbową, widzimy, że wszystkie trzy warunki spełnione są dla \(x \in (1, 3)\). Rozwiązanie: \(x \in (1, 3)\).
Przykład 3: Co zrobić, gdy po prawej stronie jest zero lub liczba ujemna?
Są to przypadki szczególne, które wymagają logicznego myślenia, a nie mechanicznego stosowania wzorów. Zawsze pamiętaj, że wartość bezwzględna dowolnego wyrażenia jest zawsze liczbą nieujemną.
Przykład A: Nierówność \(|x - 4| < -10\) Tutaj po prawej stronie mamy liczbę ujemną (\( -10 \)). Czy wartość bezwzględna może być mniejsza od liczby ujemnej? Nie! Wartość bezwzględna jest zawsze \( \geq 0 \). Zatem żadna liczba \(x\) nie spełni tej nierówności. Rozwiązanie: Brak rozwiązań, \(x \in \emptyset\).Przykład B: Nierówność \(|3x - 7| \geq 0\) Wartość bezwzględna dowolnego wyrażenia jest zawsze większa lub równa zero. Zatem ta nierówność jest zawsze prawdziwa dla każdej wartości \(x\), dla której wyrażenie \(3x-7\) jest zdefiniowane (a jest zdefiniowane dla wszystkich liczb rzeczywistych). Rozwiązanie: \(x \in \mathbb{R}\) (zbiór wszystkich liczb rzeczywistych).
Przykład C: Nierówność \(|x+2| > 0\) Ta nierówność jest prawdziwa dla wszystkich \(x\) z wyjątkiem tych, dla których \(|x+2|\) jest równe zero. \(|x+2| = 0\) tylko wtedy, gdy \(x+2 = 0\), czyli \(x = -2\). Rozwiązanie: \(x \in \mathbb{R} \setminus \{-2\}\).
Nierówności z wieloma wartościami bezwzględnymi: metoda analizy przypadków
Gdy w nierówności pojawia się więcej niż jedna wartość bezwzględna, na przykład \(|x-1| + |x+3| > 4\), proste reguły koniunkcji i alternatywy przestają wystarczać. W takich sytuacjach musimy zastosować metodę analizy przypadków, która polega na podziale osi liczbowej na przedziały i rozwiązaniu nierówności w każdym z nich. To bardziej złożona technika, ale przy odpowiedniej systematyczności staje się bardzo efektywna.
Krok 1: Wyznaczanie miejsc zerowych: klucz do podziału na przedziały
Pierwszym krokiem jest znalezienie miejsc zerowych dla każdego wyrażenia znajdującego się pod wartością bezwzględną. Miejsca zerowe to te wartości \(x\), dla których wyrażenie pod modułem przyjmuje wartość zero. Te miejsca zerowe dzielą oś liczbową na przedziały, w których znak każdego z wyrażeń pod modułem jest stały. Na przykład, dla \(|x-1| + |x+3|\), miejsca zerowe to \(x=1\) i \(x=-3\). Dzielą one oś na przedziały: \( (-\infty, -3) \), \( [-3, 1) \) i \( [1, \infty) \).Krok 2: Analiza znaków wyrażeń w każdym z wyznaczonych przedziałów
Dla każdego z wyznaczonych przedziałów musisz określić znak każdego wyrażenia pod wartością bezwzględną. Jeśli wyrażenie jest dodatnie lub równe zero, opuszczasz moduł bez zmiany znaku. Jeśli wyrażenie jest ujemne, opuszczasz moduł, zmieniając znak całego wyrażenia na przeciwny (czyli mnożysz je przez \( -1 \)). To jest kluczowy moment, który pozwala "pozbyć się" wartości bezwzględnych i przekształcić złożoną nierówność w prostsze, liniowe formy.
Krok 3: Rozwiązywanie prostszych nierówności w poszczególnych przedziałach
W każdym przedziale otrzymasz teraz prostą nierówność liniową (lub inną, ale bez wartości bezwzględnych). Rozwiązujesz ją standardowymi metodami. Bardzo ważne jest, aby pamiętać o warunku przynależności rozwiązania do danego przedziału! Ostatecznym rozwiązaniem dla danego przedziału jest część wspólna rozwiązania uzyskanej nierówności i samego przedziału. Jeśli rozwiązanie nierówności wykracza poza granice przedziału, w którym ją analizowałeś, to nie jest ono częścią rozwiązania ogólnego w tym przedziale.
Krok 4: Sumowanie rozwiązań z każdego przedziału: finałowy wynik
Po rozwiązaniu nierówności w każdym z przedziałów i znalezieniu rozwiązań cząstkowych dla każdego z nich, musisz zsumować wszystkie te rozwiązania cząstkowe. Ponieważ analizowaliśmy różne przypadki, które razem pokrywają całą oś liczbową, ostateczny zbiór rozwiązań nierówności jest sumą wszystkich poprawnych rozwiązań uzyskanych w poszczególnych przedziałach. Zazwyczaj przedstawia się go jako sumę przedziałów.

Unikaj najczęstszych błędów w nierównościach z wartością bezwzględną
Nawet doświadczeni uczniowie i studenci potrafią popełniać błędy w rozwiązywaniu nierówności z wartością bezwzględną. Z mojego doświadczenia wynika, że pewne pomyłki powtarzają się nagminnie. Świadomość tych pułapek to już połowa sukcesu, bo pozwoli Ci ich świadomie unikać. Przyjrzyjmy się najczęstszym z nich.
Błąd #1: Mylenie "i" oraz "lub" (koniunkcja vs alternatywa)
To chyba najczęstszy błąd. Wielu uczniów myli, kiedy należy stosować koniunkcję ("i" część wspólna) i kiedy alternatywę ("lub" suma przedziałów). Przypomnę:
- Dla nierówności typu \(|wyrażenie| < a\) (oraz \( \leq \)) stosujemy koniunkcję: \( -a < wyrażenie < a\). Szukamy części wspólnej rozwiązań.
- Dla nierówności typu \(|wyrażenie| > a\) (oraz \( \geq \)) stosujemy alternatywę: \( wyrażenie > a \) LUB \( wyrażenie < -a \). Szukamy sumy rozwiązań.
Błędne zastosowanie prowadzi do zupełnie innego zbioru rozwiązań. Na przykład, dla \(|x| > 2\) prawidłowe jest \(x > 2\) LUB \(x < -2\). Błędne zastosowanie koniunkcji (\(x > 2\) I \(x < -2\)) dałoby zbiór pusty, co jest oczywiście nieprawdą.
Błąd #2: Zła zmiana znaku nierówności przy opuszczaniu modułu
Pamiętaj o definicji wartości bezwzględnej: \(|x| = x\) dla \(x \geq 0\) oraz \(|x| = -x\) dla \(x < 0\). Kiedy opuszczasz moduł, a wyrażenie w środku jest ujemne, musisz zmienić jego znak. Często widzę, jak uczniowie zapominają o tym minusie lub zmieniają znak nierówności zamiast znaku wyrażenia. Przykładowo, jeśli \(x-1\) jest ujemne, to \(|x-1|\) staje się \( -(x-1) \), czyli \( -x+1 \), a nie \( x+1 \) i nie \( x-1 \) z odwróconym znakiem nierówności.Błąd #3: Problemy z poprawnym zaznaczaniem i odczytywaniem przedziałów na osi
Oś liczbowa to Twoje najlepsze narzędzie do wizualizacji rozwiązania, ale tylko wtedy, gdy używasz jej poprawnie. Często widzę błędy w:
- Użyciu nawiasów: okrągłe nawiasy \( (a, b) \) oznaczają przedział otwarty (bez punktów krańcowych), kwadratowe \( [a, b] \) przedział zamknięty (z punktami krańcowymi). Odpowiada to znakom \( <, > \) oraz \( \leq, \geq \).
- Zaznaczaniu kółek: otwarte kółka na osi dla przedziałów otwartych, zamalowane dla zamkniętych.
- Znajdowaniu części wspólnej/sumy: prawidłowe określenie, gdzie przedziały się pokrywają (dla "i") lub gdzie się łączą (dla "lub").
Precyzja w tym zakresie jest kluczowa, ponieważ nawet drobny błąd w zapisie może zmienić całe rozwiązanie.

