Często zastanawiamy się, dlaczego ruszenie ciężkiego przedmiotu z miejsca wymaga znacznie większego wysiłku niż utrzymanie go w ruchu. To zjawisko, choć powszechne, ma swoje głębokie fizyczne podstawy, które są kluczowe dla zrozumienia wielu procesów w otaczającym nas świecie. W tym artykule, jako Igor Lis, przybliżę Ci mechanizmy stojące za tarciem statycznym i kinetycznym, odpowiadając na pytanie, które z nich ma większą wartość i dlaczego jest to tak istotne w praktyce.
Tarcie statyczne jest zawsze większe niż kinetyczne poznaj kluczowe różnice i ich przyczyny
- Tarcie statyczne to siła, którą trzeba pokonać, aby wprawić ciało w ruch z miejsca.
- Tarcie kinetyczne to siła oporu, która działa, gdy ciało jest już w ruchu.
- Współczynnik tarcia statycznego (μs) dla danej pary powierzchni jest zawsze większy niż współczynnik tarcia kinetycznego (μk).
- Główną przyczyną tej różnicy są mikroskopowe nierówności powierzchni, które w spoczynku "zakleszczają się" mocniej, wymagając większej siły do ich przełamania.
- Siła tarcia statycznego maksymalnego to T_s(max) = μs * N, a kinetycznego T_k = μk * N, gdzie N to siła nacisku.
- Zjawisko to ma kluczowe znaczenie w fizyce i jest widoczne w wielu codziennych sytuacjach, np. przy przesuwaniu ciężkich przedmiotów czy działaniu systemów ABS.
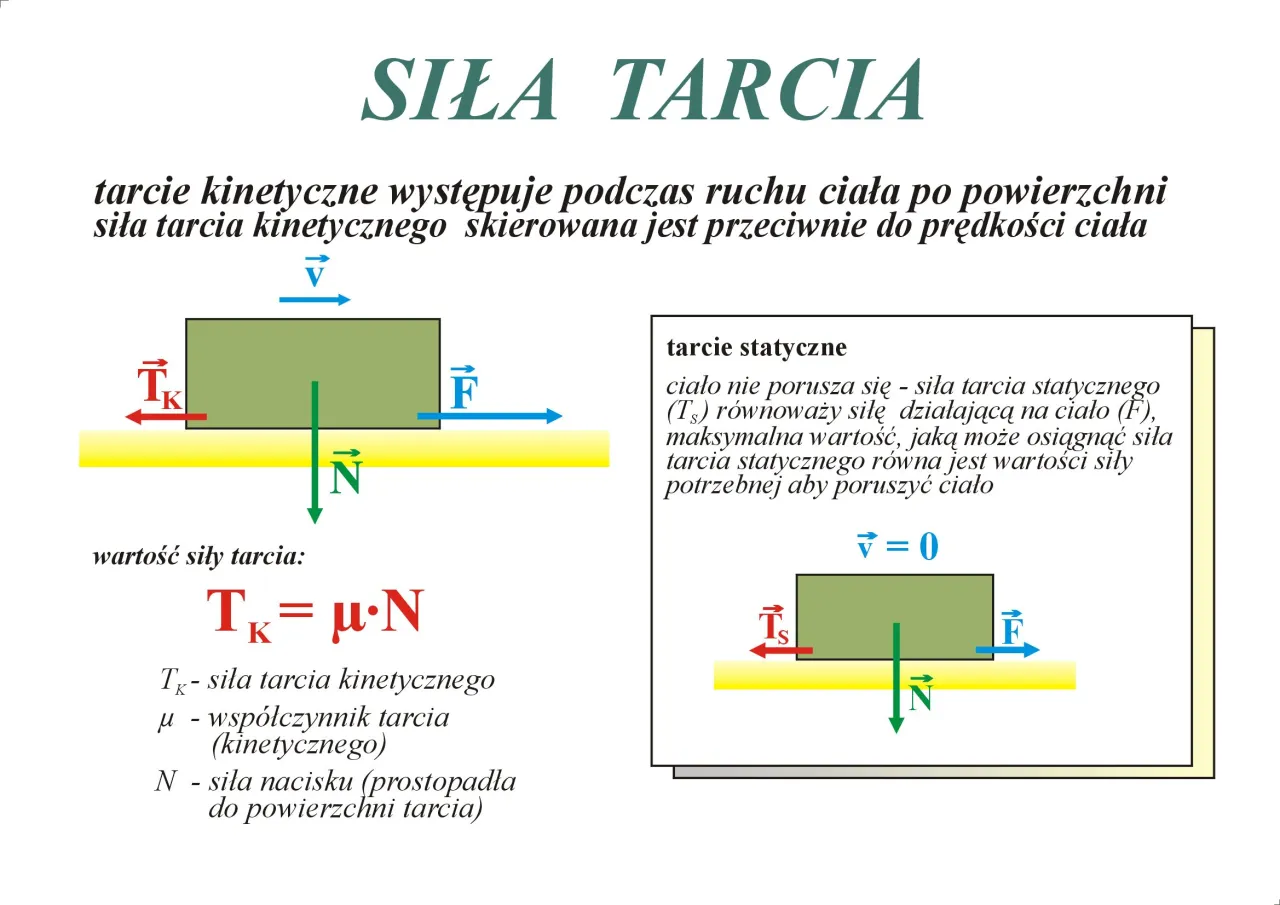
Zanim zagłębimy się w szczegóły, przypomnijmy sobie, czym jest siła tarcia w ogólnym sensie. Tarcie to siła oporu, która pojawia się na styku dwóch powierzchni i przeciwstawia się ruchowi jednego ciała względem drugiego lub próbie tego ruchu. Jest to siła kontaktowa, która odgrywa fundamentalną rolę w naszym codziennym życiu od chodzenia, przez jazdę samochodem, aż po działanie maszyn.
Tarcie statyczne to siła, która musi zostać pokonana, aby obiekt zaczął się poruszać z miejsca. Wyobraź sobie, że próbujesz przesunąć ciężki stół. Dopóki stół nie drgnie, siła, którą na niego działasz, jest równoważona przez tarcie statyczne. Co ciekawe, tarcie statyczne nie jest stałe może przyjmować różne wartości, od zera aż do pewnej wartości maksymalnej, dostosowując się do siły, którą przykładasz. Dopiero gdy przyłożona siła przekroczy tę maksymalną wartość tarcia statycznego, obiekt zacznie się poruszać.
Z kolei tarcie kinetyczne, zwane również tarciem dynamicznym, działa, gdy obiekt jest już w ruchu. Jest to siła, która dąży do spowolnienia obiektu lub utrudnienia jego dalszego ruchu. W przeciwieństwie do tarcia statycznego, tarcie kinetyczne jest zazwyczaj stałe dla danej pary powierzchni i nie zależy od prędkości (przynajmniej w typowym zakresie prędkości, z jakimi mamy do czynienia na co dzień). To właśnie tarcie kinetyczne sprawia, że po pchnięciu przedmiotu na podłodze, po pewnym czasie się on zatrzymuje.
Kto wygrywa w tym starciu? Tarcie statyczne jest zawsze większe
Przechodząc do sedna sprawy tarcie statyczne jest niemal zawsze większe niż tarcie kinetyczne. Dlaczego tak się dzieje? Odpowiedź leży w mikroskopowej strukturze powierzchni. Nawet te, które wydają się idealnie gładkie, w rzeczywistości są pełne nierówności, szczytów i dolin. Kiedy dwa ciała stykają się ze sobą i pozostają w spoczynku, te mikroskopijne nierówności jednej powierzchni mają czas, aby "zakleszczyć się" w nierównościach drugiej. Tworzą się wówczas liczne mikropołączenia, które trzeba "zerwać", aby wprawić ciało w ruch. Wymaga to znacznej siły. Gdy ciało jest już w ruchu, te nierówności nie mają wystarczająco dużo czasu, aby ponownie tak silnie się połączyć i zakleszczyć. Powierzchnie "przeskakują" jedna po drugiej, a opór jest mniejszy.
Aby ilościowo opisać te zjawiska, wprowadzamy pojęcie współczynników tarcia. Mamy współczynnik tarcia statycznego (μs) i współczynnik tarcia kinetycznego (μk). Są to bezwymiarowe wartości, które charakteryzują konkretną parę powierzchni (np. drewno na drewnie, guma na asfalcie). Kluczowa zasada, którą zawsze podkreślam moim studentom, to fakt, że dla danej pary powierzchni zawsze zachodzi zależność μs > μk. To właśnie ta nierówność jest matematycznym odzwierciedleniem tego, że ruszenie przedmiotu jest trudniejsze niż utrzymanie go w ruchu.
Siły tarcia możemy wyrazić za pomocą prostych wzorów. Maksymalna siła tarcia statycznego, czyli siła, którą musimy pokonać, aby ciało zaczęło się poruszać, wynosi:T_s(max) = μs * N
Natomiast siła tarcia kinetycznego, działająca, gdy ciało jest już w ruchu, to:
T_k = μk * N
Gdzie N to siła nacisku (siła normalna), z jaką jedna powierzchnia działa na drugą, prostopadle do płaszczyzny styku. Najczęściej jest to po prostu ciężar ciała, jeśli leży ono na płaskiej powierzchni. Jak widać z tych wzorów, ponieważ μs jest większe od μk, to i maksymalna siła tarcia statycznego jest większa niż siła tarcia kinetycznego, co doskonale odzwierciedla obserwacje z życia codziennego.
Tarcie w praktyce: jak zjawisko tarcia wpływa na nasze życie
Zrozumienie różnicy między tarciem statycznym a kinetycznym ma ogromne znaczenie w wielu aspektach naszego życia i inżynierii. Pozwól, że przedstawię kilka przykładów, które doskonale ilustrują te zasady.
Najprostszym i najbardziej intuicyjnym przykładem jest pchanie ciężkiej szafy. Z pewnością doświadczyłeś tego, że najtrudniej jest ją ruszyć z miejsca. Musisz przyłożyć znaczną siłę, aby szafa drgnęła. W tym momencie pokonujesz maksymalną siłę tarcia statycznego. Gdy już uda Ci się ją wprawić w ruch, dalsze przesuwanie staje się zauważalnie łatwiejsze. Dzieje się tak, ponieważ teraz musisz pokonywać mniejszą siłę tarcia kinetycznego.
Innym, bardzo ważnym praktycznym zastosowaniem jest działanie systemu ABS (Anti-lock Braking System) w samochodach. Głównym celem ABS jest zapobieganie blokowaniu kół podczas gwałtownego hamowania. Dlaczego? Ponieważ zablokowane koło ślizga się po nawierzchni, a wtedy działa na nie mniejsze tarcie kinetyczne. System ABS pulsacyjnie zwalnia i zwalnia koła, utrzymując je na granicy poślizgu. Dzięki temu koło wciąż się toczy (choć powoli), a między oponą a nawierzchnią działa większe tarcie statyczne. To pozwala na znacznie lepszą kontrolę nad pojazdem i skrócenie drogi hamowania, co jest kluczowe dla bezpieczeństwa.
Zjawisko tarcia jest również doskonale widoczne przy zsuwaniu się przedmiotów po równi pochyłej. Jeśli położymy przedmiot na pochyłej powierzchni, pozostanie on w spoczynku, dopóki składowa siły grawitacji (działająca wzdłuż równi) nie przekroczy maksymalnej siły tarcia statycznego. Dopiero po przekroczeniu tej wartości przedmiot zacznie się zsuwać. Co więcej, gdy już zacznie się poruszać, będzie przyspieszał, ponieważ siła oporu (tarcie kinetyczne) będzie mniejsza niż siła grawitacji działająca wzdłuż równi, co wynika z faktu, że μk < μs.
Czy tarcie statyczne jest zawsze większe? Wyjątki i obalamy mity
Chociaż zasada, że tarcie statyczne jest większe od kinetycznego, jest niemal uniwersalna i stanowi podstawę fizyki w większości zastosowań, warto wspomnieć, że istnieją bardzo specyficzne i rzadkie przypadki, gdzie ta reguła może być nieco inna. Na przykład, w niektórych polimerach, w warunkach ultra-wysokiej próżni lub przy bardzo małych obciążeniach, tarcie kinetyczne może być zbliżone lub nawet równe statycznemu. Są to jednak wyjątki od reguły, które nie dotyczą typowych zastosowań inżynierskich czy zagadnień, z którymi spotykamy się na co dzień czy w programie nauczania fizyki. W zdecydowanej większości przypadków, na przykład przy przesuwaniu mebli czy hamowaniu samochodu, tarcie statyczne jest wyraźnie większe.
Na koniec, chciałbym krótko obalić kilka popularnych mitów dotyczących tarcia:
- Powierzchnia styku: Wbrew powszechnemu przekonaniu, siła tarcia (zarówno statycznego, jak i kinetycznego) wcale nie zależy od wielkości powierzchni styku, pod warunkiem że siła nacisku pozostaje stała. Zależy ona przede wszystkim od rodzaju materiałów i siły nacisku.
- Gładkość powierzchni: Choć intuicyjnie wydaje się, że im gładsza powierzchnia, tym mniejsze tarcie, nie zawsze jest to liniowa zależność. Zbyt gładkie powierzchnie mogą prowadzić do zjawiska adhezji (klejenia się), zwiększając tarcie, zwłaszcza w warunkach próżni.
- Prędkość: Tarcie kinetyczne w typowych warunkach jest w dużej mierze niezależne od prędkości. Dopiero przy bardzo dużych prędkościach lub w specyficznych warunkach (np. bardzo niskich) mogą pojawić się zauważalne zmiany.

