Wyznaczenie środka ciężkości to fundamentalne zadanie w wielu dziedzinach od fizyki i inżynierii, po projektowanie i majsterkowanie. Ten kluczowy punkt, w którym skupiona jest cała masa obiektu, decyduje o jego stabilności i równowadze. Dla regularnych kształtów jest to proste, ale co zrobić z nieregularnymi figurami? W tym poradniku pokażę Ci praktyczne metody, które pozwolą precyzyjnie zlokalizować środek ciężkości, niezależnie od tego, czy pracujesz z fizycznym obiektem, czy z projektem na papierze.
Odkryj skuteczne metody wyznaczania środka ciężkości nieregularnych obiektów praktyczny poradnik
- Środek ciężkości to punkt, w którym skupiona jest cała masa obiektu, kluczowy dla jego stabilności i równowagi.
- Dla figur nieregularnych jego położenie nie jest intuicyjne i wymaga zastosowania specjalnych metod.
- Istnieją trzy główne grupy metod: eksperymentalne (fizyczne), analityczne (obliczeniowe) oraz komputerowe (oprogramowanie CAD, aplikacje).
- Metody eksperymentalne (np. zawieszenia) są proste i nie wymagają obliczeń, idealne dla fizycznych obiektów.
- Metody analityczne (podział na figury proste) bazują na wzorach i są stosowane dla figur na papierze lub ekranie.
- Nowoczesne programy CAD automatyzują proces, oferując najwyższą precyzję i szybkość.
Czym właściwie jest środek ciężkości i dlaczego nie zawsze pokrywa się ze środkiem geometrycznym?
Środek ciężkości to nic innego jak punkt, w którym możemy sobie wyobrazić, że skupiona jest cała masa danego obiektu. To właśnie w tym miejscu teoretycznie działa wypadkowa siła grawitacji. Dla figur o regularnych kształtach i jednorodnej gęstości, takich jak idealny kwadrat, koło czy kula, środek ciężkości pokrywa się ze środkiem geometrycznym jest to punkt symetrii. Sprawa komplikuje się jednak, gdy mamy do czynienia z nieregularnymi kształtami lub obiektami o zmiennej gęstości. Wówczas intuicja często zawodzi, a położenie środka ciężkości staje się znacznie mniej oczywiste i wymaga precyzyjnego wyznaczenia, aby zrozumieć, jak obiekt będzie się zachowywał pod wpływem sił zewnętrznych.
Praktyczne zastosowania: od stabilności konstrukcji po balans w projektach DIY
Wiedza o położeniu środka ciężkości jest niezwykle cenna i ma szerokie zastosowanie w wielu dziedzinach. Oto kilka przykładów, które pokazują, jak istotne jest jego wyznaczanie:- Stabilność konstrukcji inżynierskich: Architekci i inżynierowie muszą precyzyjnie określać środek ciężkości budynków, mostów czy innych konstrukcji, aby zapewnić ich stabilność i odporność na wiatr, trzęsienia ziemi czy inne obciążenia. Odpowiednie rozmieszczenie masy to podstawa bezpieczeństwa.
- Projektowanie pojazdów: W motoryzacji, lotnictwie czy żegludze, położenie środka ciężkości ma kluczowe znaczenie dla prowadzenia, zwrotności i bezpieczeństwa pojazdu. Niewłaściwy balans może prowadzić do przewrócenia się samochodu na zakręcie czy utraty sterowności samolotu.
- Balansowanie obiektów w projektach DIY: Jeśli budujesz model samolotu, drona, mebel, a nawet rzeźbę, musisz wiedzieć, gdzie znajduje się środek ciężkości, aby obiekt był stabilny i funkcjonalny. Zapewnienie odpowiedniego balansu to często klucz do sukcesu w amatorskich projektach.
- Sport i rekreacja: W sprzęcie sportowym, takim jak rakiety tenisowe, kije golfowe, rowery czy narty, projektanci optymalizują położenie środka ciężkości, aby poprawić wydajność i komfort użytkowania.
Różnica między środkiem ciężkości a środkiem masy kiedy można je stosować zamiennie?
Często terminy „środek ciężkości” i „środek masy” są używane zamiennie, i w większości praktycznych zastosowań na Ziemi jest to dopuszczalne. Istnieje jednak subtelna różnica. Środek masy to intrinsiczna właściwość obiektu, punkt, w którym możemy sobie wyobrazić skupienie całej jego masy, niezależnie od pola grawitacyjnego. Jest to punkt, który reprezentuje średnie położenie wszystkich cząstek tworzących obiekt. Z kolei środek ciężkości to punkt, w którym działa wypadkowa siła grawitacji. Jeśli pole grawitacyjne jest jednorodne (co jest dobrym przybliżeniem na powierzchni Ziemi dla obiektów o rozsądnych rozmiarach), środek ciężkości pokrywa się ze środkiem masy. Dopiero w bardzo dużych obiektach lub w silnie niejednorodnych polach grawitacyjnych (np. w pobliżu czarnej dziury) te dwa punkty mogłyby się różnić. W naszych codziennych, inżynierskich i edukacyjnych zastosowaniach, możemy je traktować jako tożsame.
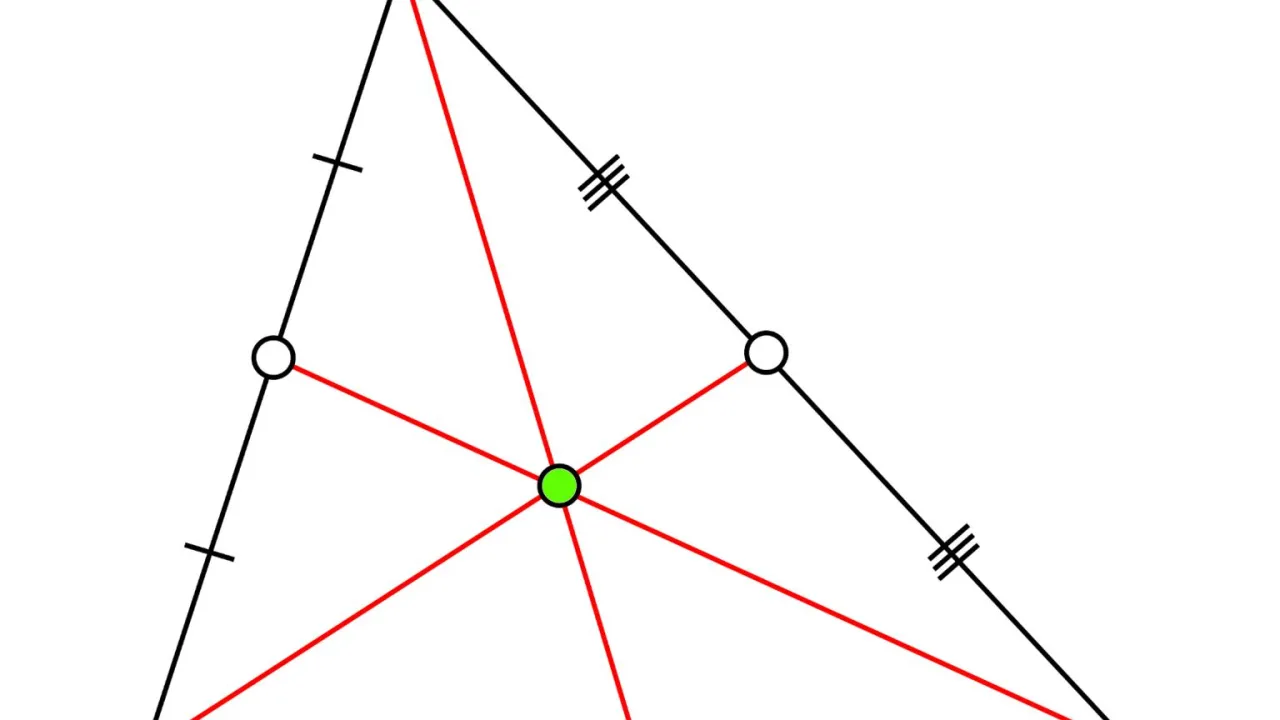
Metody eksperymentalne: znajdź środek ciężkości fizycznego obiektu
Kiedy mamy do czynienia z fizycznym obiektem, który jest nieregularny, a jego kształt trudno opisać matematycznie, metody eksperymentalne są często najprostszym i najszybszym sposobem na znalezienie środka ciężkości. Nie wymagają one skomplikowanych obliczeń, a jedynie kilku prostych narzędzi.
Krok po kroku: genialna w prostocie metoda zawieszenia (metoda linii pionu)
Metoda zawieszenia, znana również jako metoda linii pionu, to klasyczny i niezwykle efektywny sposób na wyznaczenie środka ciężkości dla płaskich, nieregularnych figur. Stosuję ją często, gdy potrzebuję szybkiego i wiarygodnego wyniku bez zagłębiania się w rachunki. Oto jak to zrobić:
- Przygotuj figurę: Upewnij się, że figura jest płaska i jednorodna (np. wycięta z kartonu, sklejki, cienkiej blachy).
- Wybierz punkty zawieszenia: Wzdłuż krawędzi figury, w co najmniej dwóch, a najlepiej trzech różnych miejscach, wykonaj małe otwory (np. dziurkaczem, szpilką). Im dalej od siebie będą te punkty, tym lepiej.
- Pierwsze zawieszenie: Przewlecz szpilkę lub gwóźdź przez jeden z otworów i zawieś figurę w taki sposób, aby mogła swobodnie się obracać.
- Użyj pionu: Przygotuj sznurek z niewielkim ciężarkiem (pion). Zawiąż sznurek na szpilce, tak aby ciężarek swobodnie zwisał wzdłuż figury. Pion wyznaczy idealnie pionową linię.
- Narysuj pierwszą linię: Gdy figura i pion ustabilizują się (przestaną się kołysać), ostrym ołówkiem narysuj na figurze linię wzdłuż sznurka pionu.
- Drugie i kolejne zawieszenie: Zdejmij figurę, a następnie zawieś ją w drugim (i ewentualnie trzecim) wybranym punkcie. Powtórz kroki 4 i 5, rysując kolejne linie pionu.
- Znajdź punkt przecięcia: Punkt, w którym wszystkie narysowane linie pionu się przecinają, jest środkiem ciężkości Twojej nieregularnej figury. To naprawdę działa!
Potrzebne narzędzia: co musisz przygotować przed rozpoczęciem?
Aby przeprowadzić metodę zawieszenia, nie potrzebujesz wiele. Większość z tych rzeczy prawdopodobnie masz już w domu lub warsztacie:
- Nieregularna figura: Płaski obiekt, którego środek ciężkości chcesz wyznaczyć (np. wycięty z kartonu, płyty MDF, plastiku).
- Sznurek z ciężarkiem (pion): Może to być zwykły sznurek z małą nakrętką, kluczem lub innym ciężarkiem na końcu. Ważne, aby był prosty i nie rozciągał się.
- Szpilka, gwóźdź lub haczyk: Coś, na czym zawiesisz figurę, umożliwiając jej swobodny obrót.
- Ołówek (najlepiej ostry): Do precyzyjnego rysowania linii.
- Dziurkacz lub ostry przedmiot: Do wykonania małych otworów w figurze.
Jak uniknąć błędów, czyli klucz do precyzji w metodzie fizycznej
Mimo prostoty metody zawieszenia, precyzja jest kluczowa. Oto kilka moich wskazówek, jak zminimalizować błędy i uzyskać jak najdokładniejszy wynik:
- Cienki sznurek: Używaj jak najcieńszego, ale nierozciągliwego sznurka do pionu. Grubszy sznurek może wprowadzać błędy w odczycie linii.
- Ostry ołówek: Precyzyjna, cienka linia jest łatwiejsza do narysowania i odczytania niż gruba, rozmazana kreska.
- Stabilne zawieszenie: Upewnij się, że figura wisi swobodnie i nie dotyka żadnych przeszkód. Poczekaj, aż całkowicie przestanie się kołysać.
- Wiele punktów zawieszenia: Zawsze zawieszaj figurę w co najmniej dwóch, a najlepiej w trzech różnych punktach. Jeśli wszystkie trzy linie przetną się w jednym punkcie, masz pewność, że wynik jest bardzo dokładny. Jeśli punkty przecięcia są rozrzucone, średnia ich położenia da Ci lepsze przybliżenie.
- Dokładne rysowanie: Staraj się rysować linię dokładnie wzdłuż sznurka, bez przesuwania figury.
Alternatywa dla zawieszania: metoda podparcia na ostrzu
Istnieje również inna metoda eksperymentalna, choć muszę przyznać, że jest ona znacznie mniej precyzyjna niż metoda zawieszenia. Mówię o metodzie podparcia na ostrzu. Polega ona na próbie zrównoważenia figury na bardzo ostrym punkcie, na przykład na czubku ołówka, igle lub krawędzi linijki. Punkt, w którym figura pozostaje w idealnej równowadze, jest jej środkiem ciężkości. Wyobraź sobie, że próbujesz zbalansować talerz na palcu to jest właśnie ta zasada. Choć jest to intuicyjne i nie wymaga żadnych narzędzi poza samym obiektem i punktem podparcia, uzyskanie precyzyjnego wyniku jest bardzo trudne, szczególnie dla większych lub cięższych obiektów. Łatwo o błędy, a punkt równowagi często jest niestabilny, dlatego osobiście zawsze preferuję metodę zawieszenia.
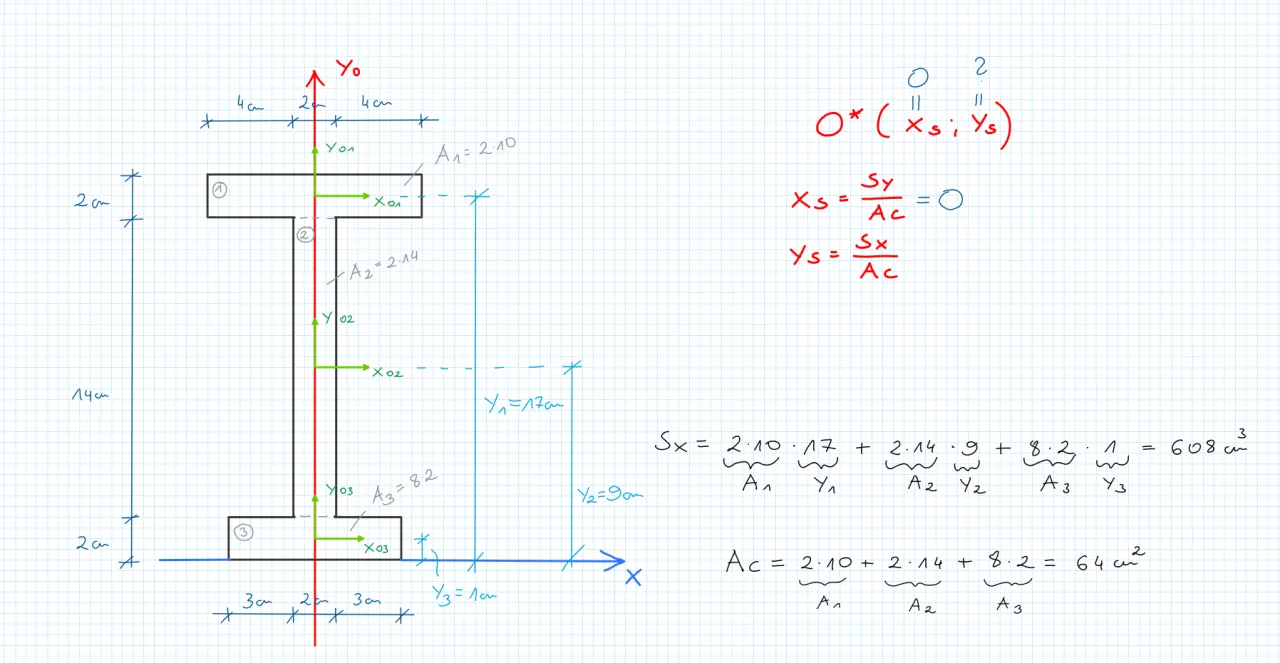
Obliczenia analityczne: wyznacz środek ciężkości figury na papierze
Kiedy nie mamy fizycznego obiektu do manipulowania, a dysponujemy jedynie jego rysunkiem lub opisem geometrycznym, musimy sięgnąć po metody analityczne. Są one bardziej precyzyjne, ale wymagają pewnych obliczeń. To podejście jest szczególnie przydatne w edukacji, inżynierii i projektowaniu, gdzie często pracujemy z abstrakcyjnymi kształtami.
Fundament obliczeń: jak podzielić skomplikowany kształt na proste figury?
Podstawą sukcesu w obliczeniach analitycznych jest umiejętność rozłożenia złożonego problemu na prostsze części. W przypadku nieregularnych figur płaskich oznacza to podzielenie ich na proste, regularne kształty, dla których położenie środka ciężkości jest powszechnie znane. Mówię tu o prostokątach, trójkątach, kołach, półkolach czy ćwiartkach koła. Środek ciężkości prostokąta leży w punkcie przecięcia przekątnych, trójkąta w punkcie przecięcia środkowych (w 1/3 wysokości od podstawy), a koła w jego geometrycznym środku. Moim zadaniem jest takie podzielenie nieregularnej figury, aby te proste części pokrywały całą jej powierzchnię bez nakładania się.
Kluczowe wzory: jak obliczyć współrzędne środka ciężkości dla układu figur?
Gdy już podzielimy naszą nieregularną figurę na prostsze elementy, możemy zastosować wzory na współrzędne środka ciężkości całego układu. Idea jest taka, że środek ciężkości całego obiektu jest "ważoną średnią" środków ciężkości jego składowych części, gdzie "wagą" jest pole powierzchni każdej części. Jeśli umieścimy naszą figurę w układzie współrzędnych (x, y), współrzędne środka ciężkości (X_c, Y_c) obliczymy następująco:
X_c = (Σ (A_i * x_i)) / Σ A_i
Y_c = (Σ (A_i * y_i)) / Σ A_i
Gdzie:
-
A_ito pole powierzchni i-tej figury składowej. -
x_ito współrzędna x środka ciężkości i-tej figury składowej. -
y_ito współrzędna y środka ciężkości i-tej figury składowej. -
Σoznacza sumę wszystkich figur składowych.
W praktyce oznacza to, że dla każdej prostej figury muszę obliczyć jej pole powierzchni i znaleźć współrzędne jej środka ciężkości. Następnie sumuję iloczyny pól i współrzędnych, a na końcu dzielę przez sumę wszystkich pól.
Przykład praktyczny: obliczamy środek ciężkości figury w kształcie litery "L"
Aby lepiej zrozumieć, jak to działa, przejdźmy przez przykład. Wyobraźmy sobie figurę w kształcie litery "L".
- Podział figury: Najprościej jest podzielić literę "L" na dwa prostokąty. Na przykład, jeden prostokąt poziomy (podstawa litery) i jeden pionowy (ramię litery).
- Ustalenie układu współrzędnych: Umieśćmy figurę w układzie współrzędnych tak, aby jej lewy dolny róg znajdował się w punkcie (0,0).
-
Określenie pól i środków ciężkości poszczególnych części:
Załóżmy, że:
-
Prostokąt 1 (podstawa): szerokość = 6 jednostek, wysokość = 2 jednostki.
- Pole A1 = 6 * 2 = 12 jednostek kwadratowych.
- Środek ciężkości (x1, y1) = (6/2, 2/2) = (3, 1).
-
Prostokąt 2 (ramię): szerokość = 2 jednostki, wysokość = 4 jednostki (od górnej krawędzi podstawy).
- Pole A2 = 2 * 4 = 8 jednostek kwadratowych.
- Środek ciężkości (x2, y2) = (2/2, 2 + 4/2) = (1, 4). (Pamiętaj, że ramię zaczyna się nad podstawą!)
Możemy to przedstawić w prostej tabeli:
Część Pole (A_i) x_i y_i A_i * x_i A_i * y_i Prostokąt 1 12 3 1 36 12 Prostokąt 2 8 1 4 8 32 Suma 20 44 44 -
Prostokąt 1 (podstawa): szerokość = 6 jednostek, wysokość = 2 jednostki.
-
Zastosowanie wzorów:
- X_c = (Σ (A_i * x_i)) / Σ A_i = 44 / 20 = 2.2 jednostki.
- Y_c = (Σ (A_i * y_i)) / Σ A_i = 44 / 20 = 2.2 jednostki.
Zatem środek ciężkości figury w kształcie litery "L" znajduje się w punkcie (2.2, 2.2).
Technika dla zaawansowanych: jak wykorzystać "ujemne pola" przy figurach z otworami?
Co zrobić, gdy nasza figura ma otwory? Na przykład, prostokąt z wyciętym w środku kołem? W takich przypadkach stosujemy sprytną technikę "ujemnych pól". Zamiast dzielić figurę na wiele małych kawałków wokół otworu, traktujemy ją jako większą, pełną figurę (np. cały prostokąt), z której "odejmujemy" otwór (np. koło). W obliczeniach analitycznych oznacza to, że pole powierzchni otworu traktujemy jako ujemne. Współrzędne środka ciężkości otworu również uwzględniamy, ale jego pole ma znak minus. Dzięki temu wzory działają poprawnie, a obliczenia są znacznie prostsze niż próba dzielenia figury na skomplikowane kształty wokół wycięcia. To eleganckie rozwiązanie, które znacznie ułatwia pracę z bardziej złożonymi geometrami.
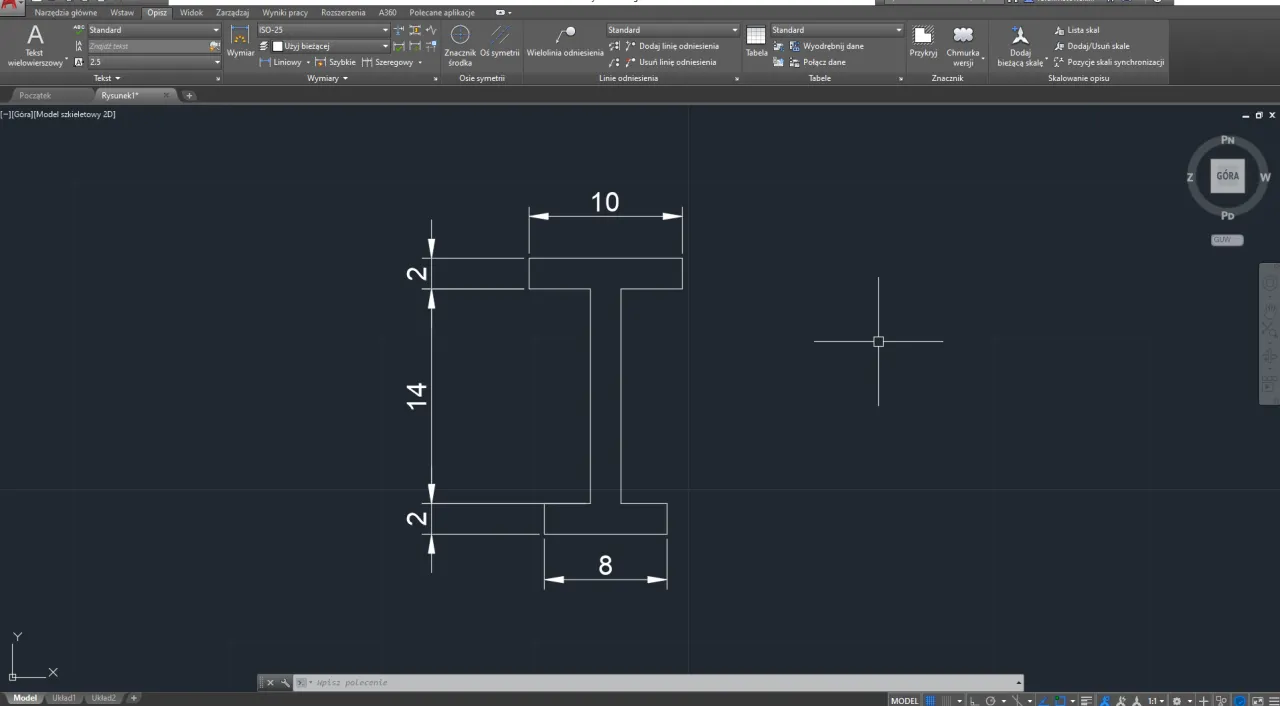
Nowoczesne technologie: szybkie i precyzyjne wyznaczanie środka ciężkości
W dzisiejszych czasach, gdy precyzja i szybkość są na wagę złota, coraz częściej sięgamy po narzędzia cyfrowe. Oprogramowanie komputerowe rewolucjonizuje sposób, w jaki podchodzimy do wyznaczania środka ciężkości, szczególnie dla bardzo złożonych kształtów.
Jak programy CAD (AutoCAD, Fusion 360) robią to za Ciebie w kilka sekund?
Dla inżynierów, projektantów i studentów kierunków technicznych, oprogramowanie CAD (Computer-Aided Design) jest niezastąpione. Programy takie jak AutoCAD, SolidWorks czy Fusion 360 posiadają wbudowane funkcje, które automatycznie obliczają właściwości geometryczne narysowanego obiektu. Wystarczy, że narysujesz swoją nieregularną figurę, a następnie wybierzesz odpowiednią opcję (często nazywaną "Mass Properties", "Area Properties" lub "Centroid"). Program w ułamku sekundy poda Ci precyzyjne współrzędne środka ciężkości (centroidu), pole powierzchni, momenty bezwładności i wiele innych parametrów. To nie tylko oszczędność czasu, ale przede wszystkim gwarancja najwyższej precyzji, której trudno byłoby osiągnąć metodami ręcznymi, zwłaszcza przy bardzo skomplikowanych kształtach 3D.
Przegląd darmowych narzędzi i aplikacji online do wyznaczania środka ciężkości
Nie każdy ma dostęp do drogiego oprogramowania CAD, ale to nie znaczy, że jesteś skazany wyłącznie na metody ręczne. Istnieje wiele darmowych narzędzi i aplikacji online, które mogą pomóc w wyznaczeniu środka ciężkości. Często są to proste kalkulatory, gdzie wprowadzasz współrzędne wierzchołków wielokąta, lub narzędzia, które pozwalają narysować kształt bezpośrednio w przeglądarce, a następnie automatycznie obliczają centroid. Wystarczy szybkie wyszukiwanie fraz takich jak "online centroid calculator" lub "środek ciężkości online", aby znaleźć wiele przydatnych zasobów. Choć mogą nie oferować takiej precyzji i funkcjonalności jak profesjonalne programy CAD, są świetnym punktem wyjścia dla studentów i hobbystów.
Czy można wyznaczyć środek ciężkości ze zdjęcia? Wprowadzenie do analizy obrazu
To już nieco bardziej zaawansowana technika, ale jak najbardziej możliwa! Wyobraź sobie, że masz zdjęcie nieregularnego obiektu i chcesz wyznaczyć jego środek ciężkości. Jest to możliwe dzięki analizie obrazu. Specjalistyczne oprogramowanie lub skrypty (często pisane w językach takich jak Python, z wykorzystaniem bibliotek do przetwarzania obrazu, np. OpenCV) potrafią przetworzyć plik graficzny. Najpierw obraz jest binaryzowany (konwertowany na czarno-biały), aby wyraźnie oddzielić obiekt od tła. Następnie algorytmy analizują rozkład pikseli tworzących obiekt i na tej podstawie obliczają jego centroid. To fascynujące zastosowanie technologii, które otwiera drzwi do automatyzacji pomiarów w wielu dziedzinach, od robotyki po kontrolę jakości.
Którą metodę wybrać? Praktyczne porównanie
Po omówieniu różnych metod wyznaczania środka ciężkości, naturalnie pojawia się pytanie: którą z nich wybrać? Odpowiedź, jak to często bywa, brzmi: to zależy. Wybór odpowiedniej metody zależy od kilku kluczowych czynników, takich jak dostępność fizycznego obiektu, wymagana precyzja, dostępność narzędzi i oprogramowania, a także złożoność samego kształtu. Nie ma jednej uniwersalnej metody, która byłaby najlepsza w każdej sytuacji.
Kiedy wystarczy prosty eksperyment, a kiedy niezbędne są precyzyjne obliczenia?
Z mojego doświadczenia wynika, że jeśli masz do czynienia z fizycznym obiektem (np. wyciętym kawałkiem materiału) i nie potrzebujesz aptekarskiej precyzji, metoda zawieszenia będzie idealna. Jest szybka, prosta i nie wymaga żadnych obliczeń. Świetnie sprawdza się w pracowniach szkolnych, warsztatach czy przy prostych projektach DIY. Jeśli jednak pracujesz z rysunkiem technicznym, planem na papierze lub ekranie, a precyzja jest kluczowa (np. w projektach inżynierskich), musisz sięgnąć po metody analityczne lub, co jeszcze lepsze, oprogramowanie CAD. Obliczenia analityczne dają bardzo dobre wyniki, ale są czasochłonne i podatne na błędy ludzkie. Programy CAD oferują najwyższą precyzję i szybkość, ale wymagają dostępu do specjalistycznego oprogramowania i umiejętności jego obsługi. Zawsze zastanów się, jaki jest Twój cel i jakie masz zasoby, zanim wybierzesz metodę.
Zestawienie zalet i wad każdej z omówionych metod
Aby ułatwić Ci wybór, przygotowałem krótkie zestawienie zalet i wad każdej z omówionych metod:
| Metoda | Zalety | Wady |
|---|---|---|
| Eksperymentalne (zawieszenia) | Proste, intuicyjne, nie wymaga obliczeń, idealne dla fizycznych obiektów. | Mniejsza precyzja (zależna od staranności), tylko dla fizycznych obiektów, nie dla projektów na papierze. |
| Analityczne (podział na figury proste) | Precyzyjne, uniwersalne dla figur na papierze/ekranie, rozwija myślenie analityczne. | Wymaga obliczeń i uwagi, czasochłonne dla złożonych kształtów, podatne na błędy obliczeniowe. |
| Komputerowe (CAD, aplikacje) | Bardzo szybkie, najwyższa precyzja, idealne dla złożonych kształtów 2D i 3D, automatyzacja. | Wymaga dostępu do oprogramowania (często płatnego), nauki obsługi, nie zawsze dostępne dla każdego. |
Przeczytaj również: Opanuj obliczanie oporu zastępczego w trudnych obwodach: Δ-Y, Kirchhoff
Najczęstsze pułapki i błędy, na które musisz uważać
Niezależnie od wybranej metody, zawsze istnieją pewne pułapki, na które warto zwrócić uwagę, aby uniknąć błędów:
- Błędy pomiarowe w metodach fizycznych: Niewłaściwe narysowanie linii pionu, niestabilne zawieszenie, użycie grubego ołówka to wszystko może prowadzić do niedokładności. Zawsze staraj się być jak najbardziej precyzyjny.
- Błędy obliczeniowe w metodach analitycznych: Pomyłki w obliczeniach pól powierzchni, błędne określenie współrzędnych środków ciężkości poszczególnych części, czy błędy w podstawieniu do wzorów to najczęstsze grzechy. Zawsze sprawdzaj swoje rachunki dwukrotnie.
- Nieprawidłowy podział figury: W metodach analitycznych kluczowe jest, aby podział na proste figury był poprawny bez nakładania się i bez pomijania żadnej części figury.
- Nieprawidłowe dane wejściowe w programach komputerowych: Nawet najlepsze oprogramowanie nie pomoże, jeśli narysujesz kształt niepoprawnie. Zawsze weryfikuj, czy geometria, którą wprowadziłeś do programu, jest zgodna z Twoimi założeniami.
- Brak zrozumienia podstaw: Niezależnie od narzędzia, zawsze warto rozumieć, czym jest środek ciężkości i dlaczego jest ważny. To pozwala na krytyczną ocenę wyników i wychwytywanie potencjalnych błędów.

