Zrozumienie zasady zachowania energii mechanicznej to jeden z kluczowych momentów w nauce fizyki. Ten artykuł to Twój praktyczny przewodnik, który pomoże Ci nie tylko zrozumieć teorię, ale przede wszystkim opanować rozwiązywanie zadań z kulką krok po kroku, przygotowując Cię do sprawdzianów i egzaminów.
Zasada zachowania energii mechanicznej w praktyce jak rozwiązywać zadania z kulką krok po kroku?
- Zasada zachowania energii mechanicznej mówi, że w układzie izolowanym (bez tarcia czy oporu powietrza) suma energii kinetycznej i potencjalnej jest stała.
- Kluczowe wzory to: energia kinetyczna `E_k = (m*v^2) / 2` oraz energia potencjalna grawitacji `E_p = m*g*h`.
- Rozwiązywanie zadań opiera się na równaniu `E_k_początkowa + E_p_początkowa = E_k_końcowa + E_p_końcowa`.
- Niezbędne jest prawidłowe określenie stanu początkowego i końcowego oraz konsekwentny wybór poziomu odniesienia `h=0`.
- Typowe zadania obejmują swobodny spadek, rzut pionowy, ruch wahadła czy staczanie się z równi pochyłej.
- W przypadku działania sił niezachowawczych (np. tarcia), energia mechaniczna nie jest zachowana, a jej ubytek jest równy pracy tych sił.
Energia, która nie bierze się znikąd: Wprowadzenie do jednej z najważniejszych zasad fizyki
Zasada zachowania energii mechanicznej to jedna z najbardziej fundamentalnych idei w fizyce, która mówi nam, że w pewnych warunkach energia nie znika ani nie pojawia się znikąd po prostu zmienia swoją formę. Wyobraź sobie układ, w którym nie ma żadnych "złodziei" energii, takich jak tarcie czy opór powietrza. W takim układzie izolowanym, gdzie działają tylko siły zachowawcze (jak grawitacja czy siła sprężystości), całkowita energia mechaniczna pozostaje stała. Oznacza to, że suma energii kinetycznej i potencjalnej w dowolnym momencie jest zawsze taka sama. Możemy to zapisać prostym, ale potężnym równaniem: `E_mech = E_k + E_p = const`.Różnica między energią kinetyczną a potencjalną: Dwa oblicza tego samego zjawiska
Kiedy mówimy o energii mechanicznej, tak naprawdę mówimy o dwóch jej głównych formach: energii kinetycznej i potencjalnej. Energia kinetyczna to energia ruchu. Pomyśl o rozpędzonym samochodzie, biegnącym człowieku czy lecącej kulce im szybciej się poruszają i im większą mają masę, tym większą posiadają energię kinetyczną. To ta energia, która pozwala im wykonywać pracę, na przykład uderzyć w coś z dużą siłą.
Z kolei energia potencjalna grawitacji to energia położenia. To energia, którą obiekt posiada ze względu na swoje miejsce w polu grawitacyjnym. Wyobraź sobie książkę leżącą na wysokiej półce ma ona energię potencjalną, bo gdy spadnie, może wykonać pracę (np. uderzyć w podłogę). Im wyżej coś się znajduje, tym większą ma energię potencjalną. Te dwie formy energii nieustannie się w siebie przekształcają, ale ich suma, w idealnych warunkach, pozostaje niezmienna.
Kluczowe równanie, które musisz znać: Jak zapisać zasadę zachowania energii?
Aby skutecznie rozwiązywać zadania, musisz opanować jedno kluczowe równanie, które jest sercem zasady zachowania energii mechanicznej. Brzmi ono: `E_k_początkowa + E_p_początkowa = E_k_końcowa + E_p_końcowa`. Co to oznacza? Po lewej stronie równania mamy całkowitą energię mechaniczną w pewnym punkcie początkowym ruchu (np. kulka na szczycie równi, zanim zacznie się staczać). Po prawej stronie mamy całkowitą energię mechaniczną w punkcie końcowym (np. kulka na dole równi). Ta zasada mówi, że całkowita energia mechaniczna w punkcie początkowym jest równa całkowitej energii mechanicznej w punkcie końcowym. To właśnie dzięki temu równaniu możemy obliczać nieznane prędkości czy wysokości, analizując przemiany energii.
Wzory, które musisz opanować
Energia ruchu, czyli energia kinetyczna (Ek) jak ją obliczyć?
Energia kinetyczna, czyli energia związana z ruchem obiektu, jest obliczana za pomocą wzoru: `E_k = (m*v^2) / 2`. W tym wzorze `m` oznacza masę obiektu (zazwyczaj podawaną w kilogramach, kg), a `v` to jego prędkość (w metrach na sekundę, m/s). Pamiętaj, że prędkość jest podnoszona do kwadratu, co oznacza, że nawet niewielki wzrost prędkości znacząco zwiększa energię kinetyczną. Jednostką energii kinetycznej, podobnie jak każdej innej energii, jest dżul (J).
Energia położenia, czyli grawitacyjna energia potencjalna (Ep) od czego zależy?
Grawitacyjna energia potencjalna, czyli energia związana z położeniem obiektu w polu grawitacyjnym, jest wyrażana wzorem: `E_p = m*g*h`. Tutaj `m` to ponownie masa obiektu (w kg), `g` to przyspieszenie ziemskie (około 9,81 m/s², często dla uproszczenia przyjmuje się 10 m/s²), a `h` to wysokość obiektu względem wybranego poziomu odniesienia (w metrach, m). Wybór poziomu odniesienia (czyli miejsca, gdzie `h=0`) jest niezwykle ważny i musi być konsekwentnie stosowany w całym zadaniu. Zazwyczaj wybiera się najniższy punkt ruchu obiektu lub powierzchnię ziemi.
Jak połączyć oba wzory w jedno działające narzędzie?
Teraz, gdy znasz już wzory na energię kinetyczną i potencjalną, możemy połączyć je w pełne równanie zasady zachowania energii mechanicznej. Podstawiając je do wcześniej wspomnianego równania, otrzymujemy: `(m*v_początkowa^2)/2 + m*g*h_początkowa = (m*v_końcowa^2)/2 + m*g*h_końcowa`. To jest właśnie to potężne narzędzie! Dzięki niemu, znając wartości w jednym punkcie ruchu i część wartości w drugim, możemy obliczyć brakujące elementy, takie jak prędkość końcowa, wysokość maksymalna czy prędkość w określonym punkcie. Kluczem jest prawidłowe zidentyfikowanie stanu początkowego i końcowego oraz konsekwentne podstawienie danych.
Rozwiązywanie zadań z kulką: Przewodnik krok po kroku
Rozwiązywanie zadań z zasadą zachowania energii mechanicznej może wydawać się skomplikowane na początku, ale z odpowiednią metodyką staje się proste i logiczne. Oto mój sprawdzony przewodnik krok po kroku:
-
Krok 1: Jak poprawnie zanalizować treść zadania i zidentyfikować dane?
Zawsze zaczynaj od dokładnego przeczytania treści zadania. Wypisz wszystkie dane, które są podane (np. masa kulki `m`, wysokość początkowa `h_początkowa`, prędkość początkowa `v_początkowa`). Zidentyfikuj również, co masz obliczyć (np. prędkość końcową `v_końcowa`, wysokość maksymalną `h_max`). Zwróć uwagę na słowa kluczowe, takie jak "puszczono swobodnie" (oznacza `v_początkowa = 0`) lub "osiągnęła maksymalną wysokość" (oznacza `v_końcowa = 0`).
-
Krok 2: Wybór kluczowego elementu gdzie ustawić poziom odniesienia (h=0)?
To jest jeden z najważniejszych kroków! Wybierz poziom, dla którego wysokość `h` będzie równa zero. Zazwyczaj najwygodniej jest wybrać najniższy punkt, do którego kulka dotrze w swoim ruchu, albo powierzchnię, na którą spadnie. Ważne jest, aby ten poziom odniesienia był konsekwentnie stosowany dla wszystkich wysokości (`h_początkowa` i `h_końcowa`) w całym zadaniu. Niewłaściwy wybór lub zmiana poziomu odniesienia w trakcie obliczeń to częsta przyczyna błędów.
-
Krok 3: Zapisanie równania energii dla punktu startowego i końcowego
Teraz czas na zapisanie pełnego równania zasady zachowania energii mechanicznej: `(m*v_początkowa^2)/2 + m*g*h_początkowa = (m*v_końcowa^2)/2 + m*g*h_końcowa`. Podstaw znane wartości i, co ważne, wyzeruj te formy energii, które w danym punkcie nie występują. Na przykład, jeśli kulka jest puszczona swobodnie, jej prędkość początkowa `v_początkowa` wynosi zero, więc człon `(m*v_początkowa^2)/2` staje się zerem. Jeśli kulka osiąga maksymalną wysokość, jej prędkość końcowa `v_końcowa` wynosi zero, więc `(m*v_końcowa^2)/2` to zero. Podobnie, jeśli kulka znajduje się na poziomie odniesienia, `h` wynosi zero, a więc `m*g*h` również.
-
Krok 4: Magia algebry, czyli jak poprawnie przekształcić wzór i znaleźć odpowiedź
Po podstawieniu wartości i wyzerowaniu zbędnych członów, zostaje Ci równanie, które należy przekształcić algebraicznie, aby wyznaczyć szukaną wielkość. Często zauważysz, że masa `m` występuje w każdym członie równania. W takim przypadku możesz śmiało podzielić całe równanie przez `m`, co znacznie uprości obliczenia i pokaże, że w wielu zadaniach masa nie ma wpływu na wynik (np. na prędkość końcową). Następnie, krok po kroku, przekształć równanie, aby wyizolować szukaną zmienną (np. `v` lub `h`). Pamiętaj o kolejności działań i dokładności obliczeń.
Przykłady zadań z kulką: Rozwiązania krok po kroku
Przejdźmy teraz do konkretnych przykładów, które pomogą Ci utrwalić wiedzę i zobaczyć, jak teoria przekłada się na praktykę.
Zadanie 1: Kulka spadająca swobodnie jak energia potencjalna zamienia się w prędkość?
Analiza sytuacji: Stan początkowy (tylko wysokość) i końcowy (tylko prędkość)
Wyobraź sobie kulkę o masie `m`, która jest puszczona swobodnie z wysokości `h` nad ziemią. Chcemy obliczyć jej prędkość w momencie uderzenia o ziemię. W punkcie początkowym (na wysokości `h`) kulka ma prędkość początkową `v_początkowa = 0` (bo jest puszczona swobodnie), więc posiada tylko energię potencjalną. W punkcie końcowym (na ziemi, gdzie `h=0`) kulka będzie miała maksymalną prędkość `v_max`, a jej energia potencjalna będzie równa zero. Cała energia potencjalna zamieni się w energię kinetyczną.
Rozwiązanie: Obliczamy prędkość końcową kulki uderzającej o podłoże
Przyjmijmy poziom odniesienia `h=0` na powierzchni ziemi. Równanie zasady zachowania energii mechanicznej to: `E_k_początkowa + E_p_początkowa = E_k_końcowa + E_p_końcowa`
Podstawiamy wzory i wartości: `0 + m*g*h = (m*v_max^2)/2 + 0`
Upraszczamy równanie, dzieląc obie strony przez masę `m` (zauważ, że masa się skraca!): `g*h = (v_max^2)/2`
Przekształcamy, aby wyznaczyć `v_max`: `v_max^2 = 2*g*h` `v_max = sqrt(2*g*h)`
Jak widać, prędkość końcowa zależy tylko od wysokości początkowej i przyspieszenia ziemskiego. Masa kulki nie ma wpływu na prędkość, z jaką uderza w ziemię (oczywiście, jeśli pominiemy opory powietrza).
Zadanie 2: Kulka rzucona pionowo w górę na jaką maksymalną wysokość się wzniesie?
Analiza sytuacji: Jak energia kinetyczna "walczy" z grawitacją?
Załóżmy, że kulka o masie `m` zostaje wyrzucona pionowo w górę z prędkością początkową `v_initial` z poziomu ziemi (`h=0`). Chcemy znaleźć maksymalną wysokość `h_max`, na jaką się wzniesie. W punkcie początkowym (na ziemi) kulka ma tylko energię kinetyczną. W momencie osiągnięcia maksymalnej wysokości `h_max`, jej prędkość chwilowo spadnie do zera (`v_końcowa = 0`), a cała energia kinetyczna zamieni się w energię potencjalną.
Rozwiązanie: Wyznaczamy wysokość maksymalną na podstawie prędkości początkowej
Przyjmijmy poziom odniesienia `h=0` na poziomie wyrzutu. Równanie zasady zachowania energii mechanicznej: `E_k_początkowa + E_p_początkowa = E_k_końcowa + E_p_końcowa`
Podstawiamy wzory i wartości: `(m*v_initial^2)/2 + 0 = 0 + m*g*h_max`
Upraszczamy równanie, dzieląc obie strony przez masę `m`: `(v_initial^2)/2 = g*h_max`
Przekształcamy, aby wyznaczyć `h_max`: `h_max = v_initial^2 / (2*g)`
Zatem, maksymalna wysokość, na jaką wzniesie się kulka, zależy od kwadratu jej prędkości początkowej i przyspieszenia ziemskiego.
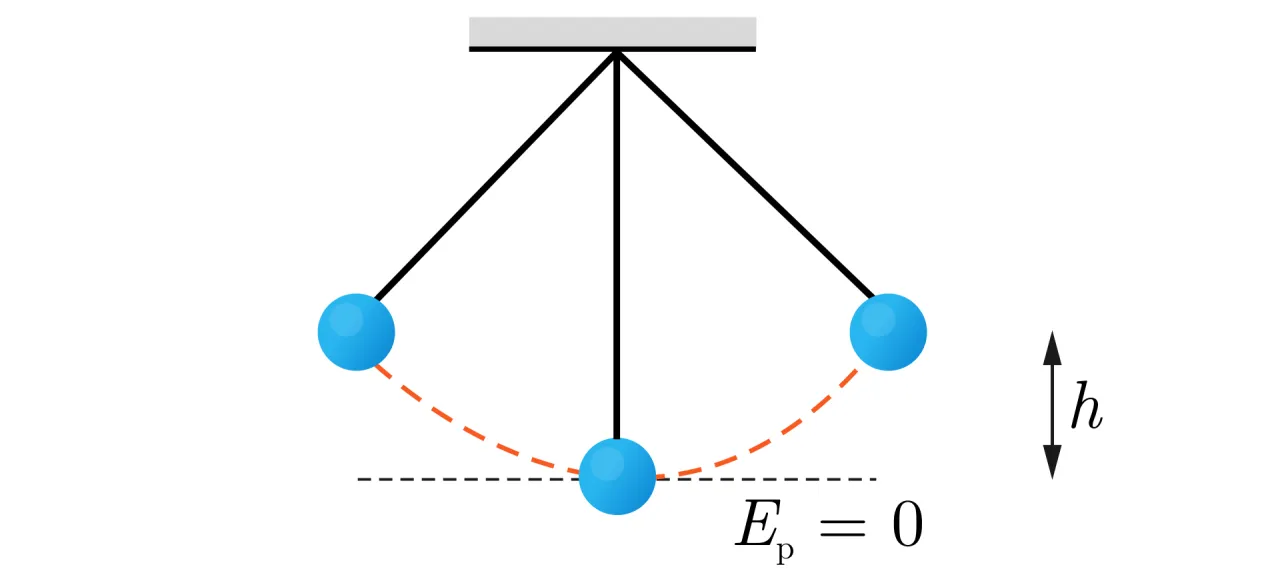
Zadanie 3: Kulka na wahadle jak obliczyć jej prędkość w najniższym punkcie?
Analiza sytuacji: Cykliczne przemiany energii w ruchu wahadłowym
Rozważmy kulkę wahadła o masie `m`, która została wychylona z położenia równowagi na pewną wysokość `h_initial` i puszczona swobodnie. Chcemy obliczyć jej prędkość `v_max` w najniższym punkcie toru (położeniu równowagi). W punkcie początkowym (na wysokości `h_initial`) kulka ma prędkość `v_początkowa = 0`, więc posiada tylko energię potencjalną. W najniższym punkcie (gdzie `h=0` względem punktu odniesienia) kulka osiągnie maksymalną prędkość `v_max`, a jej energia potencjalna będzie równa zero.
Rozwiązanie: Wykorzystanie wysokości początkowej do znalezienia prędkości maksymalnej
Przyjmijmy poziom odniesienia `h=0` w najniższym punkcie toru wahadła. Równanie zasady zachowania energii mechanicznej: `E_k_początkowa + E_p_początkowa = E_k_końcowa + E_p_końcowa`
Podstawiamy wzory i wartości: `0 + m*g*h_initial = (m*v_max^2)/2 + 0`
Upraszczamy równanie, dzieląc obie strony przez masę `m`: `g*h_initial = (v_max^2)/2`
Przekształcamy, aby wyznaczyć `v_max`: `v_max^2 = 2*g*h_initial` `v_max = sqrt(2*g*h_initial)`
Podobnie jak w zadaniu ze spadkiem swobodnym, prędkość maksymalna w najniższym punkcie wahadła zależy od wysokości, z jakiej kulka została puszczona, a nie od jej masy.
Zadanie 4: Kulka staczająca się z gładkiej równi pochyłej czy kąt nachylenia ma znaczenie?
Analiza sytuacji: Od energii potencjalnej na szczycie do energii kinetycznej na dole
Rozważmy kulkę o masie `m` puszczoną swobodnie z wierzchołka gładkiej równi pochyłej o wysokości `h`. "Gładka" oznacza, że pomijamy wszelkie tarcie. Chcemy obliczyć prędkość kulki u podstawy równi. Na szczycie równi kulka ma prędkość początkową `v_początkowa = 0`, więc posiada tylko energię potencjalną. U podstawy równi (na poziomie `h=0`) kulka osiągnie prędkość `v_max`, a jej energia potencjalna będzie równa zero.
Rozwiązanie: Dowód na to, że prędkość końcowa zależy tylko od wysokości równi
Przyjmijmy poziom odniesienia `h=0` u podstawy równi. Równanie zasady zachowania energii mechanicznej: `E_k_początkowa + E_p_początkowa = E_k_końcowa + E_p_końcowa`
Podstawiamy wzory i wartości: `0 + m*g*h = (m*v_max^2)/2 + 0`
Upraszczamy równanie, dzieląc obie strony przez masę `m`: `g*h = (v_max^2)/2`
Przekształcamy, aby wyznaczyć `v_max`: `v_max^2 = 2*g*h` `v_max = sqrt(2*g*h)`
Co ciekawe, wynik jest identyczny jak w przypadku swobodnego spadku! Oznacza to, że prędkość końcowa kulki staczającej się z gładkiej równi zależy wyłącznie od jej wysokości początkowej, a nie od kąta nachylenia równi. Kąt wpływa jedynie na czas, w jakim kulka pokona drogę, ale nie na jej prędkość końcową. To doskonały przykład elegancji zasady zachowania energii!Kiedy zasada zachowania energii mechanicznej przestaje działać?
Wszystkie dotychczasowe przykłady zakładały idealne warunki, czyli brak tarcia i oporu powietrza. W rzeczywistości jednak często mamy do czynienia z siłami, które "kradną" energię mechaniczną. Warto zrozumieć, kiedy i dlaczego zasada zachowania energii mechanicznej w swojej prostej formie nie ma zastosowania.
Siły zachowawcze i niezachowawcze: Kim są "złodzieje" energii mechanicznej?
W fizyce rozróżniamy dwa typy sił: zachowawcze i niezachowawcze. Siły zachowawcze, takie jak grawitacja czy siła sprężystości, mają tę właściwość, że praca przez nie wykonana zależy tylko od położenia początkowego i końcowego, a nie od drogi, po której porusza się obiekt. To właśnie one pozwalają na zachowanie energii mechanicznej. Natomiast siły niezachowawcze, do których zaliczamy tarcie i opór powietrza, są "złodziejami" energii mechanicznej. Wykonują one pracę, która jest zawsze ujemna (ponieważ działają przeciwnie do kierunku ruchu), a energia mechaniczna jest przez nie rozpraszana, najczęściej w postaci ciepła. To dlatego hamujący samochód nagrzewa klocki hamulcowe, a spadająca kulka rozgrzewa otaczające powietrze.
Jak uwzględnić pracę sił tarcia w równaniu energii?
Jeśli w układzie działają siły niezachowawcze, zasada zachowania energii mechanicznej musi zostać zmodyfikowana. Zamiast prostego równania `E_k_początkowa + E_p_początkowa = E_k_końcowa + E_p_końcowa`, musimy uwzględnić pracę wykonaną przez te siły. Zmodyfikowane równanie przyjmuje postać: `E_k_początkowa + E_p_początkowa = E_k_końcowa + E_p_końcowa + |W_tarcia|`. Człon `|W_tarcia|` (wartość bezwzględna pracy tarcia) reprezentuje ilość energii mechanicznej, która została rozproszona (zamieniona np. na ciepło) na skutek działania sił tarcia. Zawsze jest to ubytek energii mechanicznej, dlatego dodajemy go po stronie energii końcowej, aby równanie pozostało prawdziwe.
Praktyczny przykład: Kulka hamująca na skutek oporów ruchu
Wyobraź sobie kulkę toczącą się po szorstkim, poziomym podłożu. Na początku ma pewną energię kinetyczną. Jednak z powodu tarcia między kulką a podłożem, kulka stopniowo zwalnia, aż w końcu się zatrzymuje. Jej energia kinetyczna maleje, a ponieważ nie zmienia się jej wysokość (ruch poziomy), energia potencjalna pozostaje stała. Oznacza to, że całkowita energia mechaniczna maleje. Utracona energia kinetyczna nie znika, lecz zostaje zamieniona na ciepło, które rozgrzewa kulkę i podłoże. W tym przypadku praca sił tarcia jest równa ubytkowi energii kinetycznej.
Unikaj tych błędów: Najczęstsze pułapki w zadaniach
Jako doświadczony korepetytor, widziałem wiele błędów popełnianych przez uczniów. Oto najczęstsze z nich, na które musisz uważać:
-
Błąd #1: Mylenie poziomów odniesienia i złe wyznaczanie "h"
To absolutny klasyk! Uczeń wybiera jeden poziom odniesienia dla `h_początkowa`, a inny dla `h_końcowa`. Pamiętaj, że poziom `h=0` musi być konsekwentnie ten sam przez całe zadanie. Jeśli przyjmiesz, że ziemia to `h=0`, to kulka na wysokości 10m ma `h=10m`, a kulka w studni na głębokości 5m ma `h=-5m`. Konsekwencja to podstawa!
-
Błąd #2: Zapominanie o kwadracie przy prędkości we wzorze na energię kinetyczną
Wzór na energię kinetyczną to `E_k = (m*v^2) / 2`, a nie `m*v/2`. Pominięcie kwadratu przy prędkości `v` to prosty błąd algebraiczny, który całkowicie zmienia wynik. Zawsze sprawdzaj, czy prędkość jest podniesiona do kwadratu.
-
Błąd #3: Ignorowanie prędkości początkowej lub końcowej (gdy nie jest równa zeru)
Często uczniowie automatycznie zakładają, że prędkość początkowa lub końcowa wynosi zero. Zawsze dokładnie czytaj treść zadania! Jeśli kulka jest "puszczona swobodnie", to `v_początkowa = 0`. Jeśli "osiągnęła maksymalną wysokość", to `v_końcowa = 0`. Ale jeśli kulka ma już jakąś prędkość początkową, albo uderza w coś z prędkością inną niż zero, musisz to uwzględnić w równaniu.
Dlaczego warto opanować zasadę zachowania energii?
Podsumowanie: Energia jako uniwersalne narzędzie do opisu świata
Opanowanie zasady zachowania energii mechanicznej to nie tylko umiejętność rozwiązywania zadań z fizyki. To przede wszystkim zrozumienie jednej z najbardziej fundamentalnych i uniwersalnych zasad rządzących naszym wszechświatem. Energia jest wszechobecna i jej zachowanie pozwala nam opisywać i przewidywać zachowanie systemów fizycznych, od najmniejszych cząstek po galaktyki. To narzędzie, które otwiera oczy na to, jak działa świat.
Przeczytaj również: Obliczanie przyspieszenia z wykresu v(t) Zrozum i opanuj!
Jak zasada zachowania energii łączy różne działy mechaniki?
Zasada zachowania energii mechanicznej jest niezwykle potężna, ponieważ stanowi pomost między różnymi działami fizyki. Pozwala ona na rozwiązywanie problemów, które byłyby znacznie trudniejsze do rozwiązania za pomocą samych praw dynamiki Newtona. Upraszcza analizę ruchu, łącząc kinematykę (opis ruchu) z dynamiką (przyczyny ruchu). Co więcej, w szerszym kontekście, zasada zachowania energii mechanicznej jest częścią ogólnej zasady zachowania energii, która łączy mechanikę z termodynamiką, elektrycznością i innymi dziedzinami fizyki, pokazując spójność i piękno praw natury.

