Wyznaczanie miejsca zerowego funkcji liniowej to jedna z tych podstawowych umiejętności matematycznych, która otwiera drzwi do zrozumienia bardziej złożonych zagadnień. Dla każdego ucznia, niezależnie od etapu edukacji, opanowanie tej koncepcji i umiejętność szybkiego obliczania jej z wzoru jest absolutnie kluczowe. To nie tylko fundament pod dalszą naukę funkcji, ale także częsty element zadań egzaminacyjnych, który potrafi zadecydować o końcowym wyniku.
Jak szybko i skutecznie wyznaczyć miejsce zerowe funkcji liniowej z jej wzoru?
- Miejsce zerowe to argument (x), dla którego funkcja przyjmuje wartość zero (y=0), co graficznie oznacza punkt przecięcia wykresu z osią OX.
- Podstawową metodą wyznaczania jest przyrównanie wzoru funkcji do zera: `ax + b = 0` i rozwiązanie tego równania.
- Dla szybszych obliczeń, gdy `a ≠ 0`, możesz użyć gotowego wzoru `x₀ = -b/a`.
- Funkcja liniowa może mieć jedno, zero lub nieskończenie wiele miejsc zerowych, w zależności od wartości współczynników `a` i `b`.
- Zrozumienie i umiejętność obliczania miejsca zerowego to fundamentalna wiedza, niezbędna na egzaminach i w dalszej nauce matematyki.
Zrozumienie miejsca zerowego to klucz do funkcji liniowych
Definicja, którą musisz znać: Co to znaczy, że funkcja ma "miejsce zerowe"?
Kiedy mówimy o miejscu zerowym funkcji liniowej, mamy na myśli konkretny argument x , dla którego wartość funkcji y (lub f(x) ) wynosi dokładnie zero. To jest definicja algebraiczna, która jest fundamentem. Geometrycznie, miejsce zerowe to nic innego jak pierwsza współrzędna punktu, w którym wykres naszej funkcji liniowej, czyli prosta, przecina oś OX (oś poziomą). To jest naprawdę fundamentalna koncepcja, którą musisz opanować, aby swobodnie poruszać się w świecie funkcji.
"Wszystko powinno być tak proste, jak to tylko możliwe, ale nie prostsze." - Albert Einstein. Pamiętaj, że zrozumienie podstaw to klucz do opanowania matematyki.
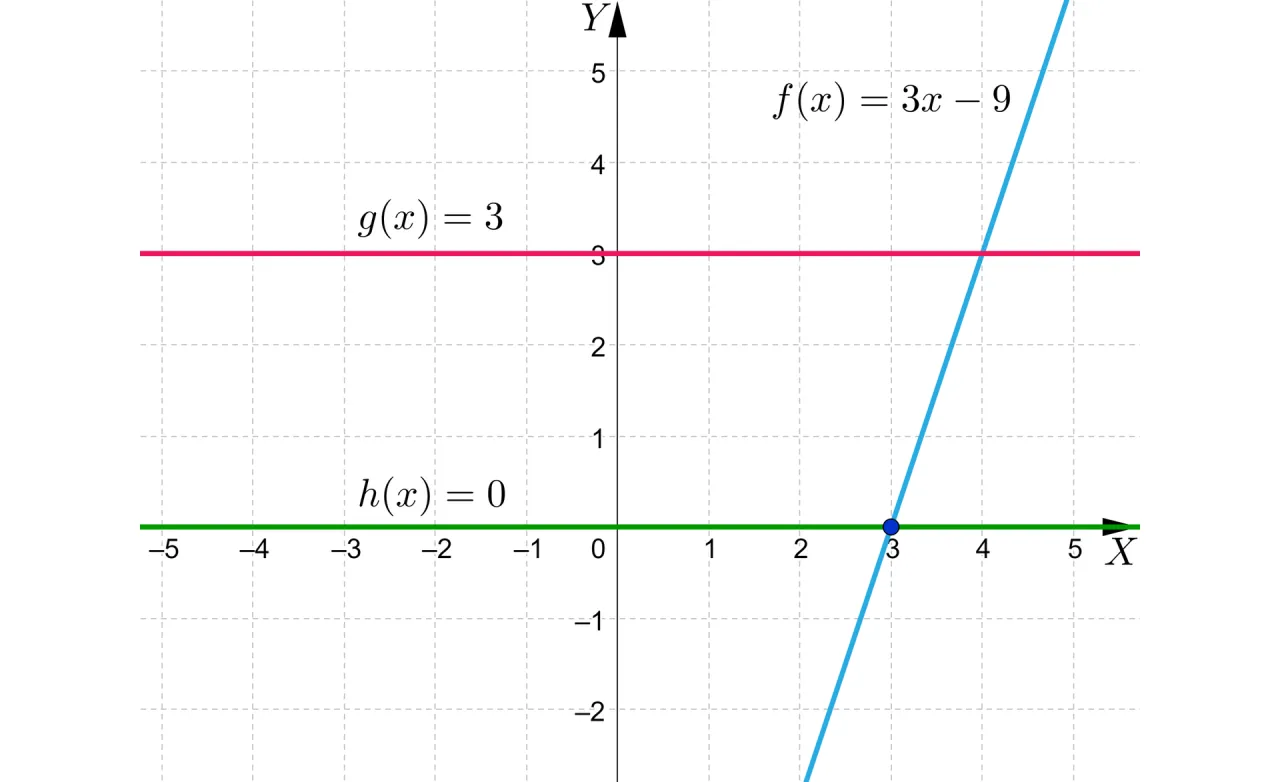
Interpretacja graficzna: Jak odczytać miejsce zerowe prosto z wykresu?
Wyobraź sobie prostą narysowaną na układzie współrzędnych. Jeśli ta prosta przecina oś OX , to punkt przecięcia jest właśnie miejscem zerowym. Konkretnie, interesuje nas współrzędna x tego punktu. Jeśli na przykład prosta przecina oś OX w punkcie (2, 0) , to miejscem zerowym funkcji jest x = 2 . To proste i intuicyjne, prawda? Zawsze warto najpierw spróbować zwizualizować sobie problem, zanim przejdziemy do obliczeń.
Dlaczego obliczanie miejsca zerowego jest tak ważne w zadaniach z matematyki?
Z mojego doświadczenia wiem, że umiejętność wyznaczania miejsc zerowych funkcji liniowej to absolutna podstawa w programie nauczania matematyki, zarówno w szkole podstawowej, jak i średniej. To zagadnienie pojawia się regularnie na egzaminie ósmoklasisty, a także jest nieodłącznym elementem zadań na maturze podstawowej. Nie chodzi tylko o samo obliczenie, ale o zrozumienie, jak zachowuje się funkcja, co jest kluczowe w rozwiązywaniu bardziej złożonych problemów, na przykład z nierównościami czy układami równań. Bez tego ani rusz!
Obliczanie miejsca zerowego krok po kroku
Metoda 1: Przyrównanie do zera niezawodny sposób dla każdego
To jest najbardziej uniwersalna i fundamentalna metoda, którą polecam opanować do perfekcji. Niezależnie od tego, z jaką funkcją liniową masz do czynienia, zawsze możesz ją zastosować. Cała idea polega na tym, że skoro miejsce zerowe to argument x , dla którego wartość funkcji y wynosi zero, to wystarczy podstawić 0 w miejsce y (lub f(x) ) do wzoru funkcji i rozwiązać powstałe równanie liniowe. Oto jak to zrobić krok po kroku:
- Zapisz wzór funkcji: Zacznij od ogólnej postaci funkcji liniowej, czyli y = ax + b .
- Przyrównaj y do zera: Zastąp y zerem, otrzymując równanie ax + b = 0 .
- Przenieś b na drugą stronę: Pamiętaj o zmianie znaku! Otrzymasz ax = -b .
- Podziel obie strony przez a : Jeśli a jest różne od zera, możesz to zrobić. Wtedy x = -b/a .
- Wynik to miejsce zerowe: Otrzymana wartość x jest szukanym miejscem zerowym.
Proste przykłady: Obliczamy miejsce zerowe dla funkcji z dodatnimi współczynnikami
Sprawdźmy to na konkretnych przykładach. Zobaczysz, że to naprawdę nic trudnego.
Przykład 1: Wyznacz miejsce zerowe funkcji y = 2x + 4 .
- Przyrównujemy do zera: 2x + 4 = 0
- Przenosimy 4 na prawą stronę: 2x = -4
- Dzielimy przez 2 : x = -4/2
- Ostateczny wynik: x = -2
Przykład 2: Wyznacz miejsce zerowe funkcji y = 3x + 6 .
- Przyrównujemy do zera: 3x + 6 = 0
- Przenosimy 6 na prawą stronę: 3x = -6
- Dzielimy przez 3 : x = -6/3
- Ostateczny wynik: x = -2
Uwaga na minusy: Przykłady z ujemnymi współczynnikami
Ujemne współczynniki często wprowadzają zamieszanie, ale jeśli będziesz uważny, nie popełnisz błędu.
Przykład 1: Wyznacz miejsce zerowe funkcji y = -2x + 6 .
- Przyrównujemy do zera: -2x + 6 = 0
- Przenosimy 6 na prawą stronę: -2x = -6
- Dzielimy przez -2 : x = -6 / (-2)
- Ostateczny wynik: x = 3 (minus przez minus daje plus!)
Przykład 2: Wyznacz miejsce zerowe funkcji y = 5x - 10 .
- Przyrównujemy do zera: 5x - 10 = 0
- Przenosimy -10 na prawą stronę: 5x = 10
- Dzielimy przez 5 : x = 10/5
- Ostateczny wynik: x = 2
Ułamki to nie problem: Jak poradzić sobie z obliczeniami na ułamkach?
Niektórzy boją się ułamków, ale ja zawsze powtarzam, że to tylko liczby. Kluczem jest pozbycie się mianowników.
Przykład 1: Wyznacz miejsce zerowe funkcji y = 1/2x + 3 .
- Przyrównujemy do zera: 1/2x + 3 = 0
- Przenosimy 3 na prawą stronę: 1/2x = -3
- Aby pozbyć się ułamka, mnożymy obie strony przez 2 : x = -3 * 2
- Ostateczny wynik: x = -6
Przykład 2: Wyznacz miejsce zerowe funkcji y = -3/4x - 2 .
- Przyrównujemy do zera: -3/4x - 2 = 0
- Przenosimy -2 na prawą stronę: -3/4x = 2
- Mnożymy obie strony przez 4 (mianownik): -3x = 8
- Dzielimy przez -3 : x = 8 / (-3)
- Ostateczny wynik: x = -8/3 (lub -2 i 2/3 )
Szybkie obliczenia miejsca zerowego za pomocą wzoru
Skąd bierze się magiczny wzór na miejsce zerowe?
Wzór na miejsce zerowe funkcji liniowej, czyli x₀ = -b/a , nie wziął się znikąd. To po prostu uproszczona forma rozwiązania równania, które zawsze tworzymy, przyrównując funkcję do zera. Zobaczmy, jak to wygląda:
- Zaczynamy od ogólnego wzoru funkcji liniowej: y = ax + b .
- Aby znaleźć miejsce zerowe, podstawiamy y = 0 : ax + b = 0 .
- Naszym celem jest wyznaczenie x , więc przenosimy b na drugą stronę równania, pamiętając o zmianie znaku: ax = -b .
- Następnie dzielimy obie strony przez a (zakładając, że a ≠ 0 ): x = -b/a .
I voilà! Mamy gotowy wzór. To nic innego jak skrócona ścieżka do tego samego wyniku, co metoda "krok po kroku".
Jak błyskawicznie obliczyć miejsce zerowe, korzystając ze wzoru?
Kiedy już znasz wzór x₀ = -b/a , obliczenia stają się naprawdę szybkie. Wystarczy zidentyfikować współczynniki a i b z wzoru funkcji i podstawić je do wzoru.
Przykład 1: Wyznacz miejsce zerowe funkcji y = 4x + 8 .
- Tutaj a = 4 i b = 8 .
- Podstawiamy do wzoru: x₀ = -8/4
- Ostateczny wynik: x₀ = -2
Przykład 2: Wyznacz miejsce zerowe funkcji y = -3x + 9 .
- Tutaj a = -3 i b = 9 .
- Podstawiamy do wzoru: x₀ = -9/(-3)
- Ostateczny wynik: x₀ = 3
Porównanie metod: Kiedy warto stosować wzór, a kiedy liczyć "na piechotę"?
Obie metody są poprawne, ale każda ma swoje zastosowanie. Ja osobiście preferuję wzór, gdy jestem pewien współczynników, ale dla początkujących metoda przyrównania do zera jest bezpieczniejsza.
| Metoda: Przyrównanie do zera (ax + b = 0) | Metoda: Wzór x₀ = -b/a |
|---|---|
| Zalety: | Zalety: |
| Uniwersalna, działa zawsze (nawet gdy a=0). | Szybka i efektywna, idealna do zadań testowych. |
| Łatwiejsza do zrozumienia dla początkujących. | Minimalizuje ryzyko błędów przy prostych obliczeniach. |
| Pomaga w budowaniu intuicji algebraicznej. | Oszczędza czas, gdy współczynniki są łatwe do zidentyfikowania. |
| Kiedy stosować: | Kiedy stosować: |
| Gdy dopiero uczysz się wyznaczać miejsca zerowe. | Gdy masz już wprawę i chcesz przyspieszyć obliczenia. |
| W zadaniach z parametrem, gdzie a może być zerem. | W zadaniach, gdzie a jest na pewno różne od zera. |
| Gdy nie jesteś pewien, jak zidentyfikować a i b . | Na egzaminach, gdy liczy się każda sekunda. |
Wyjątkowe przypadki funkcji liniowej: brak lub wiele miejsc zerowych
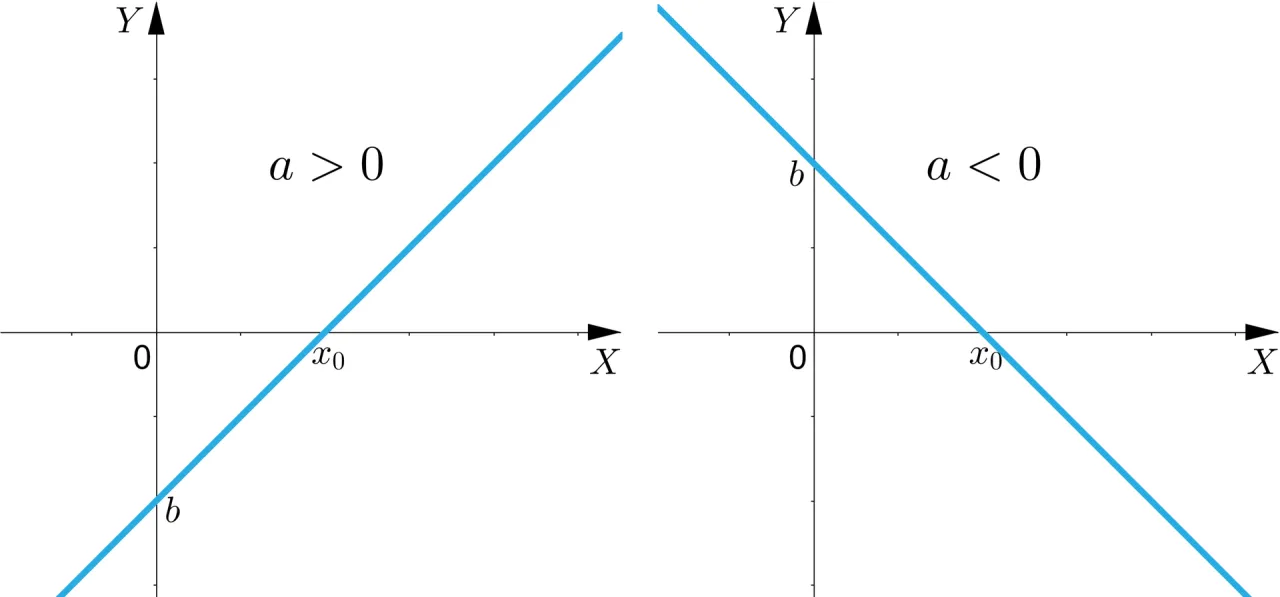
Przypadek 1: Brak miejsc zerowych czy to w ogóle możliwe?
Tak, to jest absolutnie możliwe! Funkcja liniowa nie ma miejsc zerowych wtedy, gdy jest to funkcja stała i niezerowa. Co to oznacza w praktyce? Mamy do czynienia z sytuacją, gdy współczynnik kierunkowy a jest równy zero ( a = 0 ), a wyraz wolny b jest różny od zera ( b ≠ 0 ). Wzór takiej funkcji to po prostu y = b (np. y = 3 ). Graficznie jest to prosta pozioma, która jest równoległa do osi OX , ale jej nie przecina. Skoro nie przecina, to nie ma punktów wspólnych z osią OX , a więc nie ma miejsc zerowych.
Przypadek 2: Nieskończenie wiele miejsc zerowych kiedy wykres "leży" na osi?
Ten przypadek jest jeszcze bardziej wyjątkowy. Funkcja liniowa ma nieskończenie wiele miejsc zerowych, gdy jej wykres dosłownie "leży" na osi OX . Dzieje się tak, gdy zarówno współczynnik kierunkowy a , jak i wyraz wolny b są równe zero ( a = 0 i b = 0 ). Wzór takiej funkcji to y = 0x + 0 , czyli po prostu y = 0 . Każdy punkt na osi OX ma współrzędną y = 0 , więc każdy x jest miejscem zerowym. Stąd mamy ich nieskończenie wiele.
Jak rozpoznać liczbę miejsc zerowych, patrząc tylko na wzór funkcji?
Wystarczy spojrzeć na wartości współczynników a i b :
- Jedno miejsce zerowe: Gdy współczynnik kierunkowy a ≠ 0 . To jest standardowy przypadek, gdy prosta jest nachylona i przecina oś OX w jednym punkcie.
- Brak miejsc zerowych: Gdy a = 0 i b ≠ 0 . Funkcja jest stała i niezerowa, a jej wykres jest równoległy do osi OX .
- Nieskończenie wiele miejsc zerowych: Gdy a = 0 i b = 0 . Funkcja tożsamościowo równa zeru, jej wykres pokrywa się z osią OX .
Unikaj błędów: typowe pułapki przy wyznaczaniu miejsc zerowych
Błąd nr 1: Pomyłka w znakach przy przenoszeniu "b" jak jej uniknąć?
To jest chyba najczęstszy błąd, jaki widzę u moich uczniów. Kiedy przenosisz wyraz wolny b na drugą stronę równania ax + b = 0 , musisz pamiętać o zmianie znaku! Jeśli masz +b po lewej stronie, po prawej będzie -b . Jeśli masz -b , po prawej będzie +b . To samo dotyczy stosowania wzoru x₀ = -b/a ten minus przed b jest kluczowy! Na przykład, dla funkcji y = 2x + 4 , b = 4 , więc -b = -4 . Często widzę, jak ktoś pisze x = 4/2 zamiast x = -4/2 . Zawsze sprawdź znak b we wzorze funkcji, a następnie zastosuj do niego znak przeciwny.
Błąd nr 2: Co zrobić, gdy funkcja jest w postaci ogólnej (Ax + By + C = 0)?
Czasem funkcja liniowa nie jest podana w wygodnej postaci kierunkowej y = ax + b , ale w postaci ogólnej, np. 2x + 3y - 6 = 0 . W takiej sytuacji pierwszym krokiem jest przekształcenie jej do postaci kierunkowej. Musisz wyznaczyć y z równania. Zróbmy to na przykładzie: 2x + 3y - 6 = 0 .
- Przenieś wszystkie wyrazy oprócz 3y na drugą stronę: 3y = -2x + 6 .
- Podziel całe równanie przez współczynnik przy y (czyli przez 3 ): y = (-2/3)x + 2 .
Teraz masz funkcję w postaci kierunkowej y = ax + b , gdzie a = -2/3 i b = 2 . Możesz łatwo wyznaczyć miejsce zerowe, przyrównując ją do zera: -2/3x + 2 = 0 => -2/3x = -2 => x = (-2) * (-3/2) => x = 3 .
Zadania z parametrem: Praktyczny przewodnik po zadaniach "z gwiazdką"
Zadania z parametrem m to często te "z gwiazdką", które sprawiają najwięcej kłopotów. Idea jest jednak podobna: traktujesz m jako znaną liczbę, a x jako niewiadomą. Jeśli masz funkcję typu y = (m-1)x + 2m i chcesz znaleźć jej miejsce zerowe, po prostu przyrównujesz ją do zera: (m-1)x + 2m = 0 . Następnie rozwiązujesz to równanie dla x , traktując m jako stałą: (m-1)x = -2m . Jeśli m-1 ≠ 0 (czyli m ≠ 1 ), to x = -2m / (m-1) . Jeśli m = 1 , funkcja staje się y = 2 , która nie ma miejsc zerowych. To pokazuje, jak ważne jest analizowanie warunków dla a i b , które teraz zawierają parametr m .
Szybkie podsumowanie: twoja ściągawka do miejsca zerowego
Kluczowe kroki w pigułce: Od wzoru do wyniku w 30 sekund
Aby błyskawicznie wyznaczyć miejsce zerowe funkcji liniowej, pamiętaj o tych krokach:
- Sprawdź współczynnik a : Jeśli a = 0 i b ≠ 0 , brak miejsc zerowych. Jeśli a = 0 i b = 0 , nieskończenie wiele miejsc zerowych.
- Przyrównaj do zera (metoda uniwersalna): Jeśli a ≠ 0 , podstaw y = 0 do wzoru ax + b = 0 .
- Rozwiąż równanie: Przenieś b na drugą stronę (zmień znak!) i podziel przez a .
- Użyj wzoru (metoda szybka): Alternatywnie, gdy a ≠ 0 , po prostu zastosuj x₀ = -b/a .
- Uważaj na znaki i ułamki: To najczęstsze pułapki!
Wzory i definicje, które warto zapisać i zapamiętać
Oto esencja, którą powinieneś mieć zawsze pod ręką:
- Definicja algebraiczna: Miejsce zerowe to x , dla którego y = 0 (lub f(x) = 0 ).
- Definicja geometryczna: Miejsce zerowe to pierwsza współrzędna punktu przecięcia wykresu funkcji z osią OX .
- Podstawowe równanie: ax + b = 0 (zawsze do niego dążymy!).
- Szybki wzór: x₀ = -b/a (dla a ≠ 0 ).
-
Warunki na liczbę miejsc zerowych:
- Jedno: a ≠ 0
- Brak: a = 0 i b ≠ 0
- Nieskończenie wiele: a = 0 i b = 0

