Zastanawiasz się, jak w prosty sposób odróżnić liczby pierwsze od złożonych? Ten artykuł to Twój praktyczny przewodnik, który nie tylko wyjaśni Ci podstawowe definicje, ale przede wszystkim wyposaży Cię w konkretne metody, dzięki którym samodzielnie i bez trudu sklasyfikujesz każdą liczbę naturalną. Przygotuj się na solidną dawkę wiedzy, która uporządkuje Twoje rozumienie świata liczb.
Liczby pierwsze a złożone: klucz do zrozumienia ich różnic i praktycznego rozróżniania
- Liczby pierwsze to liczby naturalne większe od 1, które mają dokładnie dwa dzielniki: 1 i samą siebie (np. 2, 3, 5).
- Liczby złożone to liczby naturalne większe od 1, które mają więcej niż dwa dzielniki i mogą być przedstawione jako iloczyn liczb pierwszych (np. 4, 6, 9).
- Liczby 0 i 1 nie są ani liczbami pierwszymi, ani złożonymi.
- Główna metoda rozróżniania to sprawdzanie podzielności przez liczby pierwsze, aż do pierwiastka kwadratowego z badanej liczby.
- Znajomość cech podzielności (przez 2, 3, 5) pozwala szybko zidentyfikować wiele liczb złożonych.
- Rozumienie liczb pierwszych ma kluczowe znaczenie w matematyce i współczesnej kryptografii, zabezpieczającej m.in. transakcje internetowe.
Zagadka liczb, czyli fundamenty matematyki w pigułce
W świecie matematyki liczby pierwsze i złożone to nic innego jak podstawowe cegiełki, z których zbudowane są wszystkie inne liczby naturalne. Ich zrozumienie jest absolutnie fundamentalne, ponieważ to właśnie na nich opiera się wiele zaawansowanych koncepcji. Można powiedzieć, że są one niczym alfabet, bez którego nie da się czytać i pisać w języku matematyki. Jako Igor Lis, zawsze podkreślam, że solidne podstawy to klucz do dalszego rozwoju, a te liczby są właśnie taką podstawą.Od szkolnej ławki po bezpieczeństwo Twoich danych w internecie
Kiedyś, w szkole, liczby pierwsze mogły wydawać się jedynie abstrakcyjnym ćwiczeniem. Dziś jednak ich praktyczne zastosowania wykraczają daleko poza podręczniki. W istocie, są one sercem współczesnej kryptografii, czyli nauki o zabezpieczaniu informacji. Algorytmy szyfrowania z kluczem publicznym, takie jak słynny RSA, opierają się właśnie na trudności w rozkładaniu bardzo dużych liczb złożonych na ich czynniki pierwsze. To dzięki nim Twoje transakcje bankowe są bezpieczne, a komunikacja internetowa chroniona przed niepowołanym dostępem. Każdego dnia, logując się do banku czy wysyłając e-mail, korzystasz z potęgi liczb pierwszych, nawet o tym nie wiedząc.
Kluczowa rola liczb pierwszych w bezpieczeństwie cyfrowym i kryptografii jest nie do przecenienia. To one stanowią fundamenty, na których opiera się zaufanie w cyfrowym świecie, chroniąc nasze dane i prywatność.
Czym jest liczba pierwsza? Prosta definicja i cechy
Zacznijmy od podstaw. Definicja liczby pierwszej jest zaskakująco prosta, a jednocześnie kryje w sobie ogromne znaczenie dla całej matematyki. To właśnie te liczby stanowią "atomowe" elementy, których nie da się dalej rozłożyć na mniejsze czynniki (poza trywialnymi).
Kluczowa zasada: tylko dwa dzielniki
Liczba pierwsza to, mówiąc najprościej, liczba naturalna większa od 1, która ma dokładnie dwa różne dzielniki naturalne: 1 i samą siebie. Ani mniej, ani więcej. To jest absolutnie kluczowa zasada. Jeśli liczba ma tylko jeden dzielnik (jak 1) lub więcej niż dwa (jak 4 czy 6), to nie jest liczbą pierwszą. Ta precyzyjna definicja pozwala nam jednoznacznie odróżnić ją od innych typów liczb.
Przykłady, które zapadną Ci w pamięć: 2, 3, 5, 7. ..
Aby lepiej to zrozumieć, przyjrzyjmy się kilku przykładom. To te liczby, które najczęściej pojawiają się w kontekście liczb pierwszych:
- 2: Dzielniki to 1 i 2.
- 3: Dzielniki to 1 i 3.
- 5: Dzielniki to 1 i 5.
- 7: Dzielniki to 1 i 7.
- 11: Dzielniki to 1 i 11.
- 13: Dzielniki to 1 i 13.
- 17: Dzielniki to 1 i 17.
- 19: Dzielniki to 1 i 19.
Jak widzisz, każda z nich spełnia warunek posiadania dokładnie dwóch dzielników.
Wyjątek potwierdzający regułę: dlaczego 2 jest tak wyjątkowa?
Wśród liczb pierwszych, dwójka jest prawdziwą gwiazdą. Dlaczego? Ponieważ jest jedyną parzystą liczbą pierwszą. Każda inna liczba parzysta (większa od 2) ma co najmniej trzy dzielniki: 1, samą siebie i 2. Na przykład 4 ma dzielniki 1, 2, 4; 6 ma 1, 2, 3, 6. Dlatego też, jeśli natkniesz się na jakąkolwiek liczbę parzystą większą od 2, możesz być pewien, że nie jest ona liczbą pierwszą. To bardzo przydatna wskazówka!
Co to jest liczba złożona? Zrozumienie drugiej kategorii liczb
Skoro poznaliśmy już liczby pierwsze, naturalne jest pytanie o ich "przeciwieństwo". Liczby złożone to druga główna kategoria liczb naturalnych (pomijając na razie 0 i 1, o których powiem później). Są one równie ważne, a ich zrozumienie jest kluczowe do pełnego obrazu.
Więcej niż dwa dzielniki, czyli na czym polega złożoność?
Liczba złożona to, podobnie jak liczba pierwsza, liczba naturalna większa od 1. Różnica polega na tym, że liczba złożona nie jest liczbą pierwszą. Oznacza to, że posiada ona więcej niż dwa dzielniki. Innymi słowy, można ją przedstawić jako iloczyn co najmniej dwóch mniejszych liczb naturalnych (innych niż 1 i ona sama). To właśnie ta "składalność" nadaje jej nazwę "złożona".
Praktyczne przykłady liczb złożonych: 4, 6, 8, 9, 10. ..
Popatrzmy na kilka przykładów, aby zobaczyć, jak to wygląda w praktyce:
- 4: Dzielniki to 1, 2, 4. Można ją zapisać jako 2 * 2.
- 6: Dzielniki to 1, 2, 3, 6. Można ją zapisać jako 2 * 3.
- 8: Dzielniki to 1, 2, 4, 8. Można ją zapisać jako 2 * 2 * 2.
- 9: Dzielniki to 1, 3, 9. Można ją zapisać jako 3 * 3.
- 10: Dzielniki to 1, 2, 5, 10. Można ją zapisać jako 2 * 5.
- 12: Dzielniki to 1, 2, 3, 4, 6, 12. Można ją zapisać jako 2 * 2 * 3.
Widać wyraźnie, że każda z tych liczb ma więcej niż dwa dzielniki i może być "rozłożona" na mniejsze czynniki.
Każda liczba złożona jako budowla z klocków: wprowadzenie do faktoryzacji
Jedną z najważniejszych właściwości liczb złożonych jest to, że każdą z nich można jednoznacznie przedstawić jako iloczyn liczb pierwszych. To fundamentalne twierdzenie arytmetyki, które nazywamy rozkładem na czynniki pierwsze (lub faktoryzacją). Wyobraź sobie, że liczby pierwsze to klocki LEGO, a liczby złożone to budowle, które z nich tworzymy. Na przykład, liczba 12 to 2 * 2 * 3. Niezależnie od tego, jak będziesz ją rozkładał, zawsze dojdziesz do tych samych "klocków" liczb 2, 2 i 3. To pokazuje, jak fundamentalne są liczby pierwsze dla całej struktury liczb naturalnych.
Jak krok po kroku odróżnić liczbę pierwszą od złożonej? Praktyczne metody
Skoro znamy już definicje, przejdźmy do sedna jak w praktyce odróżnić te dwa typy liczb? Przedstawię Ci sprawdzone metody, które pozwolą Ci samodzielnie klasyfikować liczby. To jest ta część, na którą z pewnością czekasz.
Metoda #1: Sprawdzanie podzielności - Twój niezawodny sposób
Najbardziej podstawową i niezawodną metodą jest tzw. metoda próbnych dzieleń. Oto jak to działa krok po kroku:
- Wybierz liczbę 'n', którą chcesz sprawdzić. Upewnij się, że jest to liczba naturalna większa od 1.
- Zacznij dzielić 'n' przez kolejne liczby pierwsze, począwszy od 2. Sprawdzaj, czy dzielenie jest bez reszty.
- Jeśli 'n' dzieli się bez reszty przez którąkolwiek z tych liczb pierwszych (inną niż ona sama), to 'n' jest liczbą złożoną. Gratulacje, znalazłeś czynnik!
- Kontynuuj dzielenie tylko do momentu, gdy dzielnik osiągnie wartość pierwiastka kwadratowego z 'n' (√n). To jest ten magiczny skrót, o którym zaraz opowiem.
- Jeśli po sprawdzeniu wszystkich liczb pierwszych do √n nie znajdziesz żadnego dzielnika, to 'n' jest liczbą pierwszą. Oznacza to, że ma tylko dwa dzielniki: 1 i samą siebie.
Magiczny skrót: dlaczego wystarczy sprawdzać dzielenie do pierwiastka z liczby?
Pewnie zastanawiasz się, dlaczego wspomniałem o pierwiastku kwadratowym. To nie jest żadna magia, a sprytne matematyczne uproszczenie, które oszczędza mnóstwo czasu. Jeśli liczba złożona 'n' ma dzielnik 'd', to musi mieć też drugi dzielnik 'n/d'. Jeśli 'd' jest większe od √n, to 'n/d' musi być mniejsze od √n. To oznacza, że jeśli liczba 'n' ma jakikolwiek dzielnik większy od √n, to na pewno ma też dzielnik mniejszy od √n. Dlatego wystarczy sprawdzić tylko te dzielniki, które są mniejsze lub równe pierwiastkowi kwadratowemu z badanej liczby. Jeśli do tego momentu nie znajdziemy żadnego dzielnika, to już go nie znajdziemy. Proste i genialne!
Metoda #2: Wykorzystaj cechy podzielności i oszczędzaj czas (przez 2, 3, 5)
Zanim zaczniesz żmudne dzielenie, możesz zastosować szybkie testy, które w wielu przypadkach od razu pozwolą Ci zidentyfikować liczbę złożoną. Znajomość cech podzielności to prawdziwy game changer:
-
Podzielność przez 2: Jeśli liczba jest parzysta i większa od 2 (czyli kończy się na 0, 2, 4, 6, 8), to jest liczbą złożoną. Pamiętaj, że 2 jest wyjątkiem.
Przykład: 24 (kończy się na 4) jest złożona. -
Podzielność przez 3: Jeśli suma cyfr liczby jest podzielna przez 3, to cała liczba jest podzielna przez 3 (i tym samym jest złożona, o ile jest większa od 3).
Przykład: 57 (5+7=12, a 12 dzieli się przez 3) jest złożona. -
Podzielność przez 5: Jeśli liczba kończy się na 0 lub 5 (i jest większa od 5), to jest podzielna przez 5 i tym samym jest złożona.
Przykład: 105 (kończy się na 5) jest złożona.
Wykorzystując te proste zasady, możesz błyskawicznie wykluczyć wiele liczb z grona potencjalnych liczb pierwszych.
Liczby 0 i 1: Wyjątki, które musisz znać
Zanim przejdziemy dalej, musimy poświęcić chwilę dwóm bardzo szczególnym liczbom: 0 i 1. Mają one unikalny status w teorii liczb i nie należą ani do kategorii liczb pierwszych, ani złożonych. To ważne, aby o tym pamiętać, by uniknąć pomyłek.
Dlaczego 1 nie jest liczbą pierwszą? Wyjaśnienie raz na zawsze
Liczba 1 nie jest liczbą pierwszą, ponieważ ma tylko jeden dzielnik (samą siebie). Pamiętasz definicję? Liczba pierwsza musi mieć dokładnie dwa różne dzielniki: 1 i samą siebie. Jedynka nie spełnia tego warunku, ponieważ 1 i "sama siebie" to w jej przypadku ta sama liczba. Dlatego też, choć wydaje się "nierozkładalna", nie kwalifikuje się jako liczba pierwsza.
Czemu 0 wypada z gry? Status zera w świecie liczb pierwszych
Liczba 0 również nie jest ani liczbą pierwszą, ani złożoną. Powodów jest kilka. Po pierwsze, definicje obu kategorii mówią o liczbach "większych od 1". Po drugie, zero ma nieskończoną liczbę dzielników (każda liczba naturalna, poza samym zerem, jest dzielnikiem zera, bo 0 podzielone przez dowolną liczbę daje 0). To sprawia, że nie pasuje do żadnej z naszych kategorii.

Sito Eratostenesa: Jak szybko znaleźć liczby pierwsze w danym zakresie?
Chociaż metoda próbnych dzieleń świetnie sprawdza się do testowania pojedynczych liczb, istnieje genialny algorytm, który pozwala szybko znaleźć wszystkie liczby pierwsze w zadanym zakresie. Mowa o Sicie Eratostenesa metodzie znanej już w starożytności, która do dziś jest niezwykle efektywna.
Na czym polega genialna metoda greckiego matematyka?
Sito Eratostenesa to metoda eliminacji, która działa w następujący sposób:
- Stwórz listę liczb naturalnych od 2 do wybranej przez siebie granicy (np. 100).
- Zacznij od pierwszej liczby na liście, czyli 2. Jest to liczba pierwsza.
- Wykreśl wszystkie wielokrotności liczby 2 (czyli 4, 6, 8, 10 itd.) z Twojej listy.
- Przejdź do następnej niewykreślonej liczby. Będzie to 3. Jest to liczba pierwsza.
- Wykreśl wszystkie wielokrotności liczby 3 (czyli 6, 9, 12 itd.). Jeśli jakaś liczba została już wykreślona (np. 6), po prostu ją pomiń.
- Kontynuuj ten proces: zawsze bierz kolejną niewykreśloną liczbę (będzie to liczba pierwsza) i wykreślaj wszystkie jej wielokrotności.
- Zakończ, gdy osiągniesz liczbę, której kwadrat jest większy niż Twoja górna granica. (Ponownie, ten sam "magiczny skrót" z pierwiastkiem kwadratowym!).
- Wszystkie liczby, które pozostały niewykreślone na liście, są liczbami pierwszymi w zadanym zakresie.
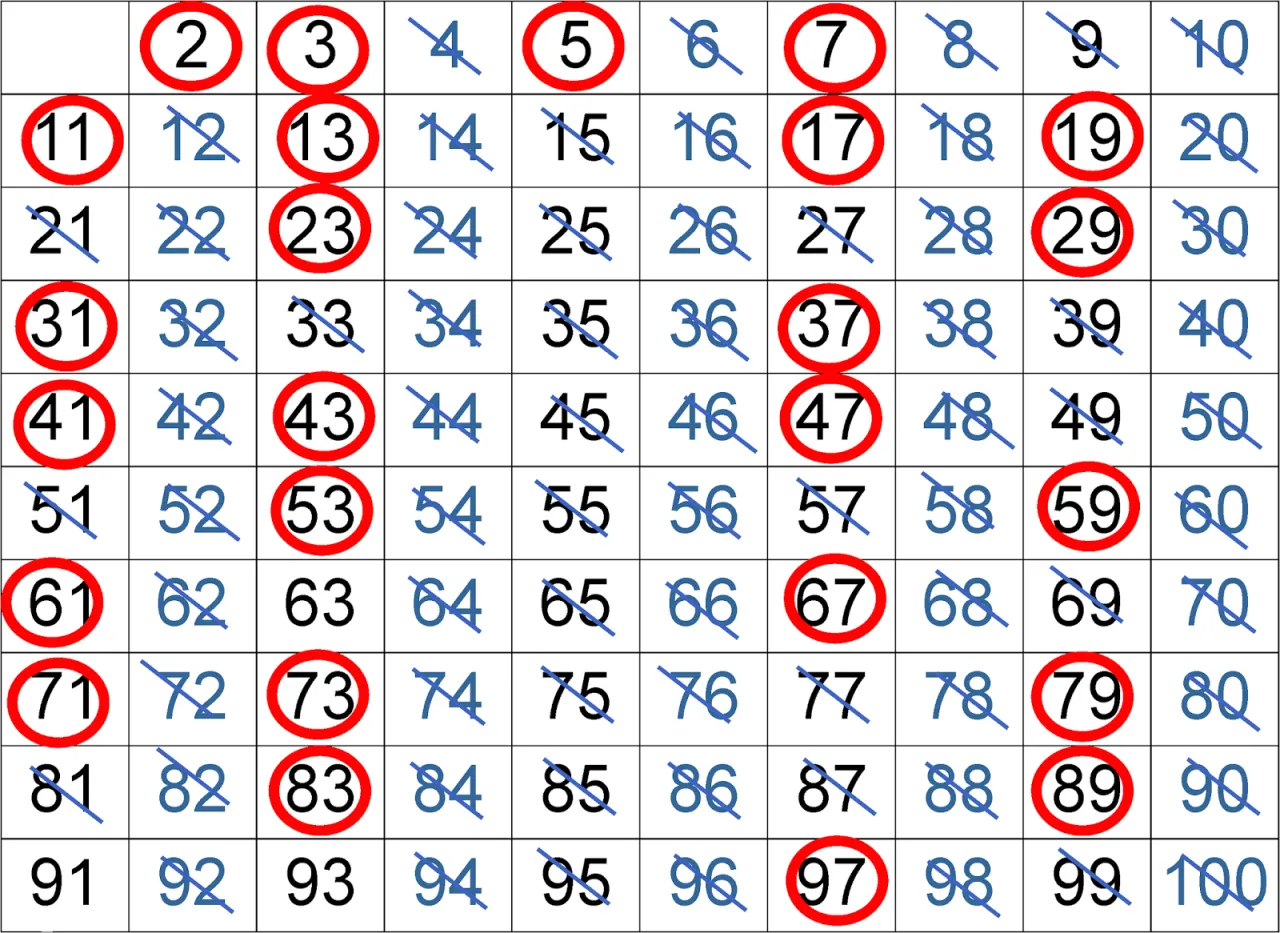
Praktyczny przykład: wyznaczamy liczby pierwsze od 1 do 100
Wyobraź sobie, że masz listę liczb od 2 do 100. Zaczynasz od 2, wykreślasz 4, 6, 8... Następnie bierzesz 3, wykreślasz 6 (już wykreślone), 9, 12... Kolejna niewykreślona to 5, wykreślasz 10, 15, 20... Potem 7, wykreślasz 14, 21, 28... Kontynuujesz ten proces, aż dojdziesz do 10 (bo 10*10 = 100, więc wystarczy sprawdzać do 7, bo 7*7=49, a następna liczba pierwsza to 11, a 11*11=121 > 100). Na koniec, liczby, które pozostaną niewykreślone, to: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97. To wszystkie liczby pierwsze do 100!
Podsumowanie: Twoja nowa umiejętność w trzech prostych krokach
Mam nadzieję, że po lekturze tego artykułu czujesz się pewniej w świecie liczb pierwszych i złożonych. Podsumujmy kluczowe kroki, które pozwolą Ci szybko i skutecznie rozróżniać te dwa typy liczb.
Krok 1: Sprawdź, czy liczba jest większa od 1
Zawsze zaczynaj od tego prostego sprawdzenia. Pamiętaj, że liczby 0 i 1 nie są ani pierwsze, ani złożone. To podstawowa zasada, która pozwoli Ci uniknąć błędów już na samym początku.
Krok 2: Użyj szybkich testów podzielności (przez 2, 3, 5)
Zanim zagłębisz się w bardziej skomplikowane obliczenia, zastosuj poznane cechy podzielności. Jeśli liczba jest parzysta (i większa od 2), suma jej cyfr dzieli się przez 3, lub kończy się na 0 bądź 5 (i jest większa od 5), to niemal na pewno jest liczbą złożoną. To szybki sposób na wyeliminowanie wielu przypadków.
Przeczytaj również: Długość okręgu z promienia? Oblicz to bezbłędnie!
Krok 3: Zastosuj metodę dzielenia do pierwiastka, by mieć 100% pewności
Jeśli szybkie testy nie dały jednoznacznej odpowiedzi, przejdź do niezawodnej metody próbnych dzieleń. Dziel badaną liczbę przez kolejne liczby pierwsze, pamiętając o "magicznym skrócie" wystarczy sprawdzać dzielniki do pierwiastka kwadratowego z liczby. Jeśli do tego momentu nie znajdziesz żadnego dzielnika, możesz być pewien, że masz do czynienia z liczbą pierwszą. To Twoja ostateczna i nieomylna weryfikacja.

